学习LCT小结

标签：基本操作   一个   make   tree   tag   就是   font   The   col   

前前言

话说前面部分大概是我一年前搞的吧。
最近又复习了一哈LCT，那就补补坑吧。
注意，为了区分，从我写spaly开始都是现在写的。

前言

首先，LCT是什么呢？
我们看看百度百科——

LCT即自动细胞学检测系统，又称液基细胞学检测系统。是宫颈筛查的一种方法。

疏松结缔组织（loose connective tissue）又称蜂窝组织（areolar tissue），其特点是细胞种类较多，纤维较少，排列稀疏。疏松结缔组织在体内广泛分布，位于器官之间、组织之间以至细胞之间，起连接、支持、营养、防御、保护和创伤修复等功能。

好吧，不是这个。
LCT即为link-cut-tree
是一种解决动态树的有效利器。
动态树是一类问题，常见的有维护树的连通性，求树上路径的极值等。

然后LCT即为一种用Splay来维护树链剖分的算法，简单理解为“支持删边、加边的动态树链剖分”

前置技能：

树链剖分https://blog.csdn.net/HiChocolate/article/details/77170675
（不会的可以看看我写的）
Splay https://blog.csdn.net/qq_30974369/article/details/77587168
（不会的可以看看不是我写的）
重点是树链剖分的全部内容加上splay的一些基本操作（如标记下传、区间翻转《排序机械臂》）

一些定义

既然百度百科没有很好的定义来学习，那我就来大致讲讲。（实际上是我懒得打定义）

LCT的本质也是树链剖分，它的树也是用很多的偏爱路径和非偏爱路径来连接起来的。
这些为了方便理解，不妨也用树链剖分的定义来定义。
1、重边连起来会组成重链，重链之间没有公共点。
我们首先跑一遍算出dfn序之后，我们就可以找到很多很多条重链。
2、那么对于一颗树，其中一条重链的点，都在一颗splay中，关键字是深度。
3、树链剖分的重链是一成不变的，但是LCT的重链是可以随意改变的。这也注定了LCT的重链需要用到splay来维护。
4、重链与重链之间的边在splay中用虚边来表示。
5、一条重链的虚边会存在它的splay的根上，指向这条重链的顶点的father所在的重链的splay的根。

就是这么多啦。
其实这样子很难理解4与5的定义什么意思，那么我们画画图。

上面加粗的边即为重边，然后连成重链。
然后，我们把每一条重链都给弄出来，对它建一颗splay，那么就变成——

那么对于上面的这个图，三角形就代表一个splay，每个splay对应着LCT上的每个链。
那么有些链是用一条轻边连起来的，那么在splay上就用一个虚边连接。
理解定义5，就会发现在这张图上，这些有向边可以表示为虚边。

然后就大致介绍完LCT的基本定义与构造了。

一些干货

由于我们的这个LCT并不需要把它建出来，只需要维护spaly即可。
因此，我们节点维护下面的一些基本值：

• fa表示当前节点spaly上的父亲
• pf表示当前节点在LCT上虚边连接的点
• son[1/0]在spaly上的儿子

关于spaly

其实spaly在LCT中只需要利用其旋转，就可以基本完成一切操作（废话）
那么在旋转过程中，需要改进的只有一个向虚边传送。
代码

void rotate(int x)
{
    int y=t[x].fa,k=get(x);
    if(t[y].fa) t[t[y].fa].son[get(y)]=x;
    if(t[x].son[!k]) t[t[x].son[!k]].fa=y;
    t[y].son[k]=t[x].son[!k],t[x].fa=t[y].fa,t[y].fa=x,t[x].son[!k]=y;
    update(y),update(x);
    t[x].pf=t[y].pf;//就在这里！！！
}

核心操作access

我们定义一个操作\(access(x)\)表示把当前x到根的所有边都变成重边，然后把这条链以外的所以边变成轻边。
具体操作看图：
（盗盗图）

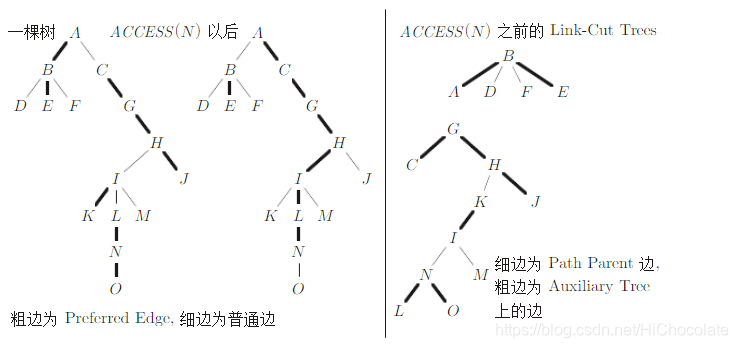
应该很好理解。
代码：

void access(int x)
{
    for (int y=0;x;update(x),y=x,x=t[x].pf)//一直跳重链
    {
        splay(x,0);
        t[t[x].son[1]].fa=0;//断掉原来的重链
        t[t[x].son[1]].pf=x;
        t[x].son[1]=y;//把下面的spaly接到上面
        t[y].fa=x;
        t[y].pf=0;
    }
}

基本操作1 makeroot

我们定义一个操作\(makeroots(x)\)表示把x变成LCT的根。
操作简单，先access一下，那么我们就可以得到一颗spaly。
然鹅这颗spaly最右边的点是x，我们要把他变成最左边。
于是把它旋转到根，翻转一下即可（翻转就是排序机械臂中的翻转）
代码：

void make(int x)
{
    swap(t[x].son[0],t[x].son[1]);
    t[x].tag^=1;
}
void makeroot(int x)
{
    access(x),splay(x,0);
    make(x);
}

基本操作2 findroot

我们定义一个操作\(findroots(x)\)表示寻找x所在树的root。
这个操作有什么用呢？
你可以用这个代替并查集，只是时间多了些
用醋很多，就不一一介绍了。

如何实现？
access(x)一下，然后我们发现x和原本的根在同一spaly上。
然后询问spaly上最左边的点即可。

int findroot(int x)
{
    access(x),splay(x,0);
    for (;t[x].son[0];x=t[x].son[0]);
    return x;
}

基本操作3 link

这个就很帅气了。
我们定义一个操作\(link(x,y)\)表示连接x和y这条边。
方法很简单，我们先makeroot(x)，然后把x连接到y即可。

void link(int x,int y)
{
    makeroot(x);
    if(findroot(y)!=x) t[x].pf=y;
}

基本操作4 cut

我们定义一个操作\(cut(x,y)\)表示删掉x和y这条边。
我们考虑makeroot(x)，然后access(y)。
如果x和y之间有连边，那么y必定是x的儿子。
断掉即可。

void cut(int x,int y)
{
    makeroot(x),access(y),splay(y,0);
    if(t[x].fa==y) t[y].son[get(x)]=t[x].fa=t[x].pf=0;
}

应用

大致就是上面的这些操作。
例题？洛谷上很多。
当然，https://blog.csdn.net/HiChocolate/article/details/101380259
这也是一个模板。

学习LCT小结

标签：基本操作   一个   make   tree   tag   就是   font   The   col   

原文地址：https://www.cnblogs.com/RainbowCrown/p/11600799.html