标签：iostream 一个 图片 ali int idt upload etc space
求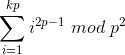 
的值，其中，k，p均为不超过109的正整数。其中保证p是质数。
一看到这种数论题，我就想：打表吧！
于是任取一个质数13，k为1,2,3,4……
打出来发现是这样的（未取余）：
91 195 312 442 585 741 （k = 1~6）
然而，这是什么规律？？
发现它们都能除13.
开心的把它们都除了13：
7 15 24 34 45 37 是不是已经发现规律了？
换了一个质数，发现它们都满足这个规律
于是大胆假设这个规律
对于一个质数p，第k项是首项为(p+1)/2，公差为1的等差数列的前缀和。
而且还发现若k>(p+1)/2，则它对p2取余后和第p-k项相等。
然后对于p=2特判一下即可。 代码如下：
#include <cstdio>
#include <iostream>
using namespace std;
inline void read (int& s) {
s = 0;
static char c = getchar ();
while (c < ‘0‘ || c > ‘9‘) c = getchar ();
while (c >= ‘0‘ && c <= ‘9‘) s = (s << 3) + (s << 1) + (c & 15), c = getchar ();
return ;
}
typedef long long ll;
ll k, p, MOD;
inline ll mult (ll p, ll x) {
ll s = 0;
while (x) {
if (x & 1) s = (s + p) % MOD;
p = (p + p) % MOD;
x >>= 1;
}
return s;
}
int main () {
cin >> k >> p;
MOD = 1ll * p * p;
if (p & 1) {
k %= p;
if (k > p / 2) k = p - k;
ll a = p + 1 >> 1;
ll x = k * a % MOD;
ll y = k * (k - 1) / 2;
x = (x + y) % MOD;
cout << mult (x, p) << ‘\n‘;
}
else putchar ((k & 1) + ‘0‘), putchar (‘\n‘);
return 0;
}
标签：iostream 一个 图片 ali int idt upload etc space
原文地址：https://www.cnblogs.com/Squirrel-Vae/p/11600556.html
