标签:bsp 一个 mamicode 并且 动态规划 技术 地方 分割 图片
问题描述
01背包问题:有n个物品,每个物品有体积和价值两个属性,现在有一个固定容量的背包,要将这些物品放入背包内,使得背包内物品总价值最大,问要如何放?
注意:每个物品的数量为1。

设$V = 14$。
为了描述方便起见,我们用$c_1,c_2,c_3,....c_n$表示物品的体积, 用$w_1,w_2,w_3,....w_n$表示物品的价值,用$V$表示背包的容量,$n$表示物品的数量。
动态规划描述
背包问题是动态规划问题的一种,和分治算法一样,它是将一个大问题分成一个一个的小问题,然后找到大问题和小问题之间的递推式,将一个个小问题组合成大问题,
并且通常要求这些小问题也要达到最优。能用动态规划解决的问题一般含有两种性质:最优子结构和重叠子问题。动态规划从本质上讲就是穷举法, 但是它的却比一般的算法效率要高,
这就是因为它能剪去重叠的子问题,使得总体复杂度不那么高。
解决方法
1.递归方法
我们先从最容易入手的地方开始,用递归的方法来解这个问题。
首先对于每个物品,我们的选择只有两个:放或者不放。我们将所有的可能都穷举出来,就可以得到下面这个树状图(只画了前四个结点):
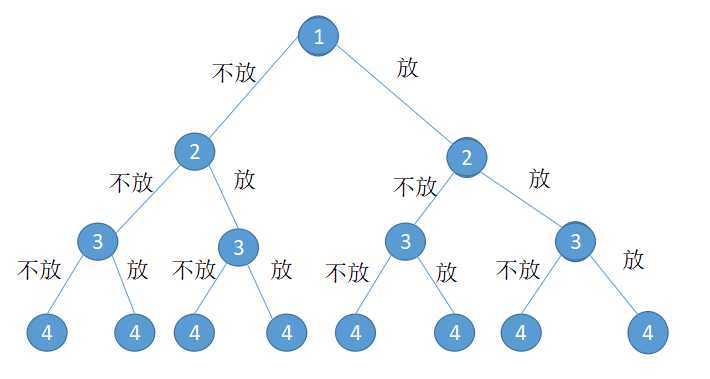
这个树上每一个分支都只能选一个,每一行就代表一个子问题。我们用$F(i, v_i)$表示前$i$个物品放入背包内的最大价值(即最优方案),此时这个$v_i$指的是放入前$i$个物品后背包剩余的容量。
显而易见$F(5, v_5)$就是我们要解的大问题,分割一下子问题就是:$F(1, v_1)$, $F(2, v_2)$, $F(3, v_3)$, $F(4, v_4)$。要解决这个大问题,我们就得先解决它的前面一个子问题$F(4, v_4)$(求解原问题时子问题也要达到最优,所以该问题具有最优子结构,这是判断问题能否用动态规划解的条件之一)。
至于为什么解决$F(5, v_5)$问题之前要先解决$F(4, v_4)$,这是因为对于问题$F(5, v_5)$来说,如果解决了问题$F(4, v_4)$剩下就只需要判断最后一个物品体积是否比剩余背包容量大,是直接放入背包,否则就不放。
而对于子问题$F(4, v_4)$,我们得解决$F(3, v_3)$....从而得解决$F(1, v_1)$。对于子问题$F(1, v_1)$,由于它前面没有子问题,所以解决它只需要判断$c_1 \le V$是否成立。
所以对于每一个子问题,由于前面的子问题已被解决,因此我们都只需要做两个选择:放,还是不放。
假设我们已经知道了前$i-1$个物品放入背包的最优方案$F(i-1, v)$,那么对于第$i$个物品要放入背包就有三种情况:
若物品的体积$c_i$大于背包剩余的容量$v$,那么只能丢弃这个物品:
$F(i, v_i) = F(i-1, v_i-1)$
否则就有两种选择:
1. 不放第$i$个物品:
$F(i, v_i) = F(i-1, v_i-1)$
2. 放第$i$个物品:
$F(i, v_i) = w_i + F(i-1, v_i-1-c_i)$
要从这两个方案中选择总价值最大的,所以:
$$
F(i, v_i) =
\begin{cases}
F(i-1, v_{i-1}), & \text{ $c_i > v_{i-1}$ } \\
max(F(i-1, v_{i-1}), w_i +F(i-1, v_{i-1}-c_i)), & \text{ $c_i \le v_{i-1}$ }
\end{cases}
$$
用Python实现代码如下:
#递归求解 def rec_bag(c, w, v, i): ‘‘‘ param c: 物品体积 param w: 物品价值 param v: 当前背包剩余容量 param i: 当前物品编号 return: 背包装下物品的最大价值 ‘‘‘ if i > len(c)-1: return 0 elif v <= 0: #体积不能为负 return 0 elif v > 0: if c[i] <= v: A = w[i] + rec_bag(c, w, v-c[i], i+1) B = rec_bag(c, w, v, i+1) res = max(A, B)#两种方案中选最优的那个并返回 else: res = rec_bag(c, w, v, i+1)#物品体积大于背包容量,直接返回 return res
代码我没有测试过,如果有错误可以在评论区告诉我。
后面动态规划解法和另外两个问题有时间再补充。
标签:bsp 一个 mamicode 并且 动态规划 技术 地方 分割 图片
原文地址:https://www.cnblogs.com/Alevals/p/11600947.html