[CSP-S模拟测试]:u（差分）

标签：异或   数组   模拟   include   sharp   输入格式   $1   can   c++   

题目背景

　　$\frac{1}{4}$遇到了一道水题，完全不会做，于是去请教小$D$。小$D$看了一眼就切掉了这题，嘲讽了$\frac{1}{4}$一番就离开了。于是，$\frac{1}{4}$只好来问你，这道题是这样的：

题目描述

　　考虑一个$n\times n$的矩阵$A$，初始所有元素均为$0$。
　　执行$q$次如下形式的操作给定$4$个整数$r,c,l,s$，对于每个满足$x\in [r,r+l),y\in [c,x−r+c]$的元素$(x,y)$，将权值增加$s$。也就是，给一个左上顶点为$(r,c)$、直角边长为$l$的下三角区域加上$s$。
　　输出最终矩阵的元素异或和。

输入格式

从文件$u.in$中读入数据。
第一行两个整数$n,q$。
接下来$q$行，每行四个整数$r,c,l,s$，代表一次操作。

输出格式

输出到文件$u.out$中。
输出一行，一个整数，代表答案。

样例

样例输入：

10 4
1 1 10 1
5 5 4 4
1 9 4 3
3 3 5 2

样例输出：

0

数据范围与提示

样例解释：

1 0 0 0 0 0 0 0 3 0
1 1 0 0 0 0 0 0 3 3
1 1 3 0 0 0 0 0 3 3
1 1 3 3 0 0 0 0 3 3
1 1 3 3 7 0 0 0 0 0
1 1 3 3 7 7 0 0 0 0
1 1 3 3 7 7 7 0 0 0
1 1 1 1 5 5 5 5 0 0
1 1 1 1 1 1 1 1 1 0
1 1 1 1 1 1 1 1 1 1

数据范围：

保证$n\in [1,{10}^3],q\in [0,3\times {10}^5],r,c,l\in [1,n],s\in [1,{10}^9]$。

题解

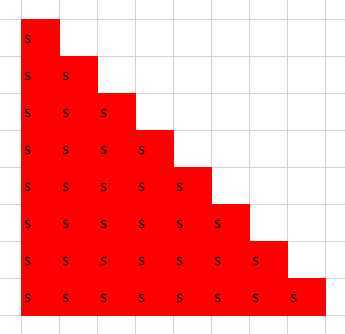
对于每次操作，相当于将下图中红色区域都加了$s$：

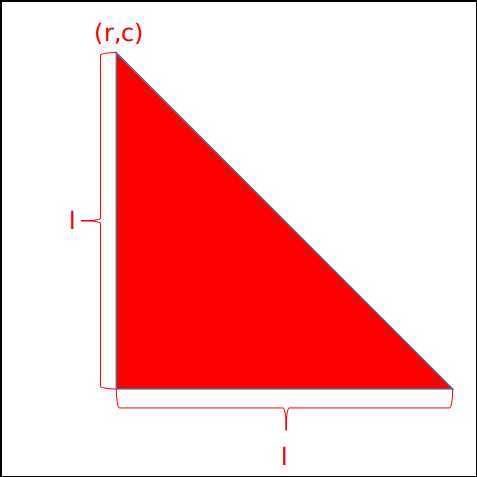
看数据范围显然只允许我们$\Theta(1)$修改。

那么我们就想到了差分。

如何差分呢？

我们维护两个差分数组，一个是对于列的差分（设为$s1$数组）；另一个是对于斜着的差分（设为$s2$数组），如下图：

这样的话，就简单多了，对于每一个操作，我们只需要将$s1[r][c]+s$，$s1[r+l][c]-s$，$s2[r][c+1]-s$，$s2[r+l][c+l+1]+s$即可，如下图。

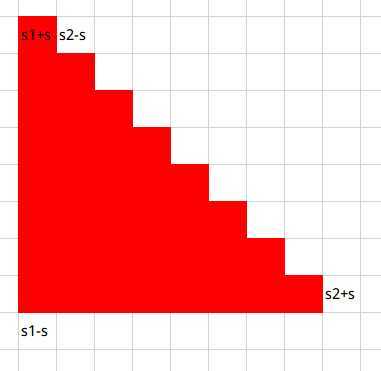
然后我们再令$s1[i][j]+=s1[i-1][j]$，$s2[i][j]+=s2[i-1][j-1]$即可变成这样，为方便，再定义$s3$数组表示整个矩阵从左到右的差分：

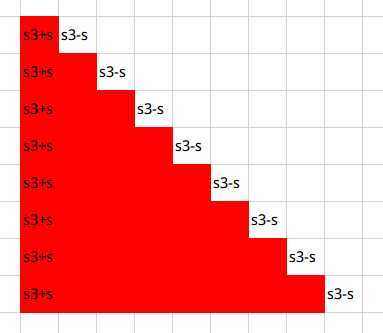
对其取前缀和就得到了最后的矩阵：

最后，记得开$long\ long$，否则只有$1$分不要怪我……

时间复杂度：$\Theta(n^2+q)$。

期望得分：$100$分。

实际得分：$100$分。

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n,q;
long long s1[1010][1010],s2[1010][1010];
long long ans;
int main()
{
	scanf("%d%d",&n,&q);
	while(q--)
	{
		int r,c,l,s;
		scanf("%d%d%d%d",&r,&c,&l,&s);
		s1[r][c]+=s;
		if(c+1<=n)s2[r][c+1]-=s;
		if(r+l<=n)
		{
			s1[r+l][c]-=s;
			if(c+l+1<=n)s2[r+l][c+l+1]+=s;
		}
	}
	for(int i=1;i<=n;i++)
	{
		long long sum=0;
		for(int j=1;j<=n;j++)
		{
			s1[i][j]+=s1[i-1][j];
			s2[i][j]+=s2[i-1][j-1];
			sum+=s1[i][j]+s2[i][j];
			ans^=sum;
		}
	}
	printf("%lld",ans);
	return 0;
}

rp++

[CSP-S模拟测试]:u（差分）

标签：异或   数组   模拟   include   sharp   输入格式   $1   can   c++   

原文地址：https://www.cnblogs.com/wzc521/p/11602403.html