标签：uil   快速   通过   def   while   节点   n+1   实现   mamicode   

算法简介

扫描线算法用于求许多矩形的面积并。

算法流程

基本思想

对于一堆矩形，我们从下往上用一根水平的直线扫过去，把面积一块一块扫出来。从最下面一条矩形横边开始，每一块矩形面积，为直线扫到此处被矩形覆盖的长度乘以该直线到下一条横边的高度差。这个很好理解，看图说话：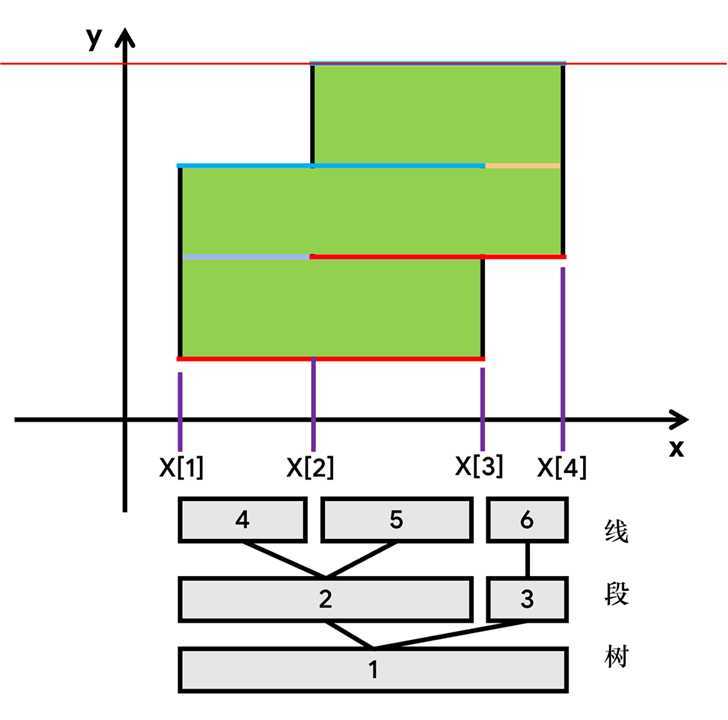
思想就很简单易懂。

实现？

如何快速找扫描线长度？
我们把所有横边按照\(y\)排序，并且把它们的端点的\(x\)离散化，设离散化后\(i\)对应的原值为\(X[i]\)。
从下往上扫，一个矩形下面的称为入边，权值为\(1\)，上面的为出边，权值为\(-1\)。
我们的线段树，每一个节点的左右为\(l、r\)的话，它维护的就是\(X[l]~X[r+1]\)这个扫描线上的区间（以保证每个节点维护的都是一个区间，且不会重叠）。每扫描到一条横边，如果是入边，线段树上对应节点\(+1\)，如果是出边就\(-1\)，这样该节点的数就代表扫描线对应的区间此时覆盖上的矩形数。如果不为0，该区间覆盖长度为区间长度，直接算就行；如果为0，说明该区间没有被完全覆盖，其被覆盖长度必须由其子节点更新（子节点没有完全覆盖就继续递归下去，叶子节点中间没有别的竖边，所以要么完全覆盖要么完全没被覆盖）。这样维护就搞定扫描线长度了。
令每个横边扫描线长度为\(len[i]\)，则\(ans=\sum_{i=1}^{n-1} {len[i]*(y[i+1]-y[i])}\)，大功告成。

代码

模板(洛谷P5490)

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,X[1000001],Y[1000001],cnt,ans;
struct Ju{
    int l,r,y,f;
}a[1000001];
int a1,b1,a2,b2;
struct Tr{
    int l,r,sum,v;
}tr[4000001];
inline int Read()
{
    int x=0,f=1;
    char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-')
          f=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        x=(x<<3)+(x<<1)+ch-'0';
        ch=getchar();
    }
    return x*f;
}
void Write(int x)
{
    if(x<0)
    {
        putchar('-');
        x=-x;
    }
    if(x>9)
      Write(x/10);
    putchar(x%10+'0');
}
inline bool cmp(Ju a,Ju b)
{
    return a.y<b.y;
}
void Build(int x,int l,int r)
{
    tr[x].l=l,tr[x].r=r;
    if(l==r)
      return;
    int mid=(l+r)>>1;
    Build(x<<1,l,mid);
    Build(x<<1|1,mid+1,r);
}
inline void Pushup(int x)
{
    int l=tr[x].l,r=tr[x].r;
    if(tr[x].sum)
      tr[x].v=X[r+1]-X[l];
    else 
      tr[x].v=tr[x<<1].v+tr[x<<1|1].v;//区间是否被覆盖没有可加性，例如两个子区间有覆盖，但没覆盖整个区间，那这个区间的值还是0
      //如果两个区间都有覆盖，且覆盖了整个区间，这个区间的值却为0，怎么办？
      //就通过pushdown来保证区间覆盖长度的正确性
}
void Add(int x,int l,int r,int k)
{
    //if(l>=X[tr[x].r+1]||r<=X[tr[x].l])
    //  return;
    if(l<=X[tr[x].l]&&r>=X[tr[x].r+1])
    {
        tr[x].sum+=k;
        Pushup(x);
        return;//每次查询总是从节点1开始查询，所以对于整个覆盖的区间，子区间不会被查询，就不修改了
    }
    int mid=(tr[x].l+tr[x].r)>>1;
    if(l<=X[mid])
      Add(x<<1,l,r,k);
    if(r>X[mid+1])
      Add(x<<1|1,l,r,k);
    Pushup(x);//没覆盖整个区间就要修改子区间了
}
signed main()
{
    n=Read();
    for(register int i=1;i<=n;++i)
    {
        a1=Read(),b1=Read(),a2=Read(),b2=Read();
        a[(i<<1)-1].y=b1,a[(i<<1)-1].l=a1,a[(i<<1)-1].r=a2,a[(i<<1)-1].f=1;
        a[i<<1].y=b2,a[i<<1].l=a1,a[i<<1].r=a2,a[i<<1].f=-1;
        X[(i<<1)-1]=a1,X[i<<1]=a2;
    }
    n=n<<1;
    sort(X+1,X+n+1);
    cnt=unique(X+1,X+n+1)-X-1;
    sort(a+1,a+n+1,cmp);
    Build(1,1,cnt-1);
    for(register int i=1;i<=n;++i)
    {
        Add(1,a[i].l,a[i].r,a[i].f);
        ans+=tr[1].v*(a[i+1].y-a[i].y);
    }
    Write(ans);
}

扫描线

标签：uil   快速   通过   def   while   节点   n+1   实现   mamicode   

原文地址：https://www.cnblogs.com/SKTT1Faker/p/11600730.html