标签:现象 为什么 art 通过 http 布尔值 存储 就是 cab
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法。而我们所想要实现的留言过滤其实是一种分类行为,是通过对于概率的判断,来对样本进行一个归类的过程。
朴素贝叶斯分类(NBC)是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法,先通过已给定的训练集,以特征词之间独立作为前提假设,学习从输入到输出的联合概率分布,再基于学习到的模型,输入A求出使得后验概率最大的输出B。
朴素贝叶斯公式:
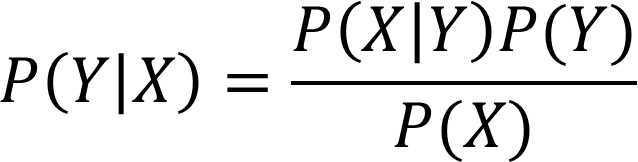
或者说:
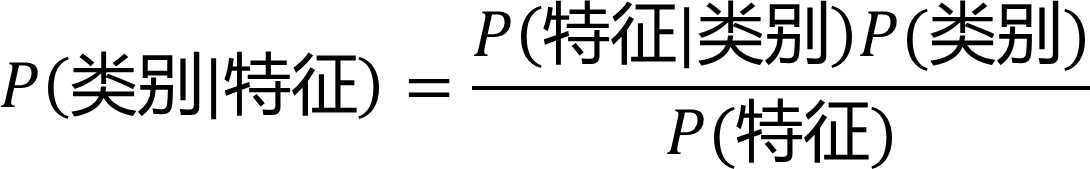

当我们假设各项条件之间是相互独立的,比如说“我觉得你很美”“他觉得你很美”,不论是“我”还是“他”觉得“你很美”都是无关的,并不会因为是谁来评价而影响这个评价,那么它就适合用朴素贝叶斯算法。
举一个很典型的例子,假设通过一些指标如长相、性格等来判断一个人我们是否要嫁给他,有这样一个表格:
| 长相 | 性格 | 身高 | 是否上进 | 结果 |
| 帅 | 坏 | 低 | 不上进 | 不嫁 |
| 丑 | 好 | 低 | 上进 | 不嫁 |
| 帅 | 好 | 低 | 上进 | 嫁 |
| 丑 | 好 | 高 | 上进 | 嫁 |
| 帅 | 坏 | 低 | 上进 | 不嫁 |
| 丑 | 坏 | 低 | 不上进 | 不嫁 |
| 帅 | 好 | 高 | 不上进 | 嫁 |
| 丑 | 好 | 高 | 上进 | 嫁 |
| 帅 | 好 | 高 | 上进 | 嫁 |
| 丑 | 坏 | 高 | 上进 | 嫁 |
| 帅 | 好 | 低 | 不上进 | 不嫁 |
| 帅 | 好 | 低 | 不上进 | 不嫁 |
这时当我们遇到一个小伙子并且我们知道以上条件:长相丑,性格坏,身高低,不上进,现在就可以转换成一个数学上的分类问题来比较 P(嫁|各项条件) 与 P(不嫁|各项条件) 谁的概率大我们就能给出嫁或者不嫁的答案。然而,我们需要保证这些条件之间没有关联,我们发现比如一个人美丑与他是否上进、一个人性格好坏和他身高之间是无关的,所以适用于朴素贝叶斯公式的条件,那么久可以进行计算了。
经过统计:
p(嫁) = 6/12(总样本数) = 1/2
p(丑|嫁) = 3/6 = 1/2
p(坏|嫁)= 1/6
p(低|嫁) = 1/6
p(不上进|嫁) = 1/6
p(丑) = 1/3
p(坏) = 1/3
p(低) = 7/12
p(不上进) = 1/3
我们带入公式P(嫁|丑、坏、低、不上进)=P(丑、坏、低、不上进|嫁)*P(嫁)/P(丑、坏、低、不上进)=[P(丑|嫁)*P(坏|嫁)*P(低|嫁)*P(不上进|嫁)] / [P(丑)*P(坏)*P(低)*P(不上进)]= (1/2*1/6*1/6*1/6*1/2)/(1/3*1/3*7/12*1/3)
下面我们根据同样的方法来求P(不嫁|丑、坏、低、不上进)= ((1/6*1/2*1*1/2)*1/2)/(1/3*1/3*7/12*1/3)
由于P(嫁|丑、坏、低、不上进)<P(不嫁|丑、坏、低、不上进),所以我们得出结论 不嫁。
假如没有这个假设,那么我们对右边这些概率的估计其实是不可做的,这么说,我们这个例子有4个特征,其中帅包括{帅,丑},性格包括{不好,坏},身高包括{高,低},上进包括{不上进,上进},那么四个特征的联合概率分布总共是4维空间,总个数为2*2*2*2=16个。在现实生活中,有非常多的特征,每一个特征的取值非常多,那么通过统计来估计后面概率的值,变得几乎不可做,这是为什么需要假设特征之间独立的原因。假如我们没有假设特征之间相互独立,那么我们统计的时候,就需要在整个特征空间中去找,将会更多,比如我们就需要在嫁的条件下,去找四种特征全满足的人的个数,这样的话,由于数据的稀疏性,很容易统计到0的情况。 这样是不合适的。
零概率问题:在计算新实例的概率时,如果某个分量在训练集中从没出现过,会导致整个实例的概率计算结果为0。针对文本分类就是当一个词语在训练集中没有出现过,那么该词语的概率是0,使用连乘法计算文本出现的概率时,整个文本出现的概率就也是0,得到的结果就会非常不合理!
我们是不是可以对这种数据采用加一来解决?
法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率,所以加1平滑也叫做拉普拉斯平滑。就是对于一个离散的值我们在使用的时候不是直接输出它的概率,而是对概率值进行“平滑” 处理。即默认所有的特征都出现过一次,将概率改成下面的形式 其中 N 是全体特征的总数。

如由如下训练数据学习一个朴素贝叶斯分类器并确定??=(2,??)^??的类标记,特征:??1,??2,取值的集合分别是{1,2,3},{S,M,L},类标记:Y∈{−1,1}:
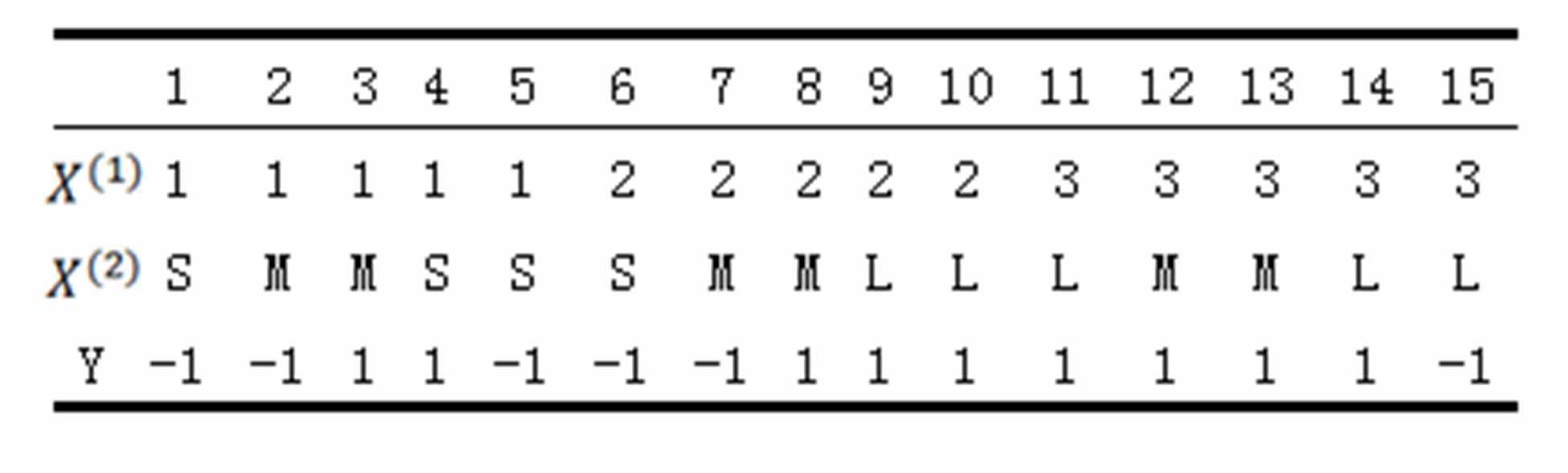
这还不够,如果由于结果需要对很多个很小的数作乘法,则可能会出现下溢的情况,所以在进行处理的时候可以对概率的乘积取自然对数,根据自然对数函数的单调性,不会改变最终的大小关系,但是很好的防止了下溢出的问题。
首先要明确我们的训练集由正常的文档和侮辱性的文档组成,能反映侮辱性文档的是侮辱性词汇的出现与否以及出现频率。
这样的模型有以下两种:
那么我们就要对样本进行预处理和对训练数据向量化,现在对于中文分词,分词工具有很多种,比如说:jieba分词、thulac、SnowNLP等,这里我们使用结巴分词。安装:
$ pip install jieba
之后我们还需要用到python的numpy包。安装:
$ pip install numpy
下面展示实例代码:
去除停用词:
import jieba # 创建停用词列表 def stopwordslist(): stopwords = [line.strip() for line in open(‘chinsesstoptxt.txt‘,encoding=‘UTF-8‘).readlines()] return stopwords # 对句子进行中文分词 def seg_depart(sentence): # 对文档中的每一行进行中文分词 print("正在分词") sentence_depart = jieba.cut(sentence.strip()) # 创建一个停用词列表 stopwords = stopwordslist() # 输出结果为outstr outstr = ‘‘ # 去停用词 for word in sentence_depart: if word not in stopwords: if word != ‘\t‘: outstr += word outstr += " " return outstr
#停用词库可以百度搜索下载
留言过滤:
import numpy as np import jieba class isgentry(): def __init__(self,testWords): self.testWords=testWords def loadData(self): wordList=[ [‘你‘,‘傻逼‘], [‘我‘,‘朋友‘,‘她‘,‘很‘,‘厉害‘], [‘你‘,‘看起来‘,‘非常‘,‘聪明‘,‘我‘,‘喜欢‘,‘你‘], [‘她‘,‘很‘,‘恶心‘],
[‘弱智‘],[‘愚蠢‘],[‘狗‘],[‘神经病‘],[‘笨蛋‘],[‘脑残‘],[‘垃圾‘],[‘丑‘],[‘讨厌‘], [‘美丽‘],[‘睿智‘],[‘好‘],[‘赞‘],[‘博学‘],[‘漂亮‘],[‘实用‘],[‘爱‘] ]
# 训练样本内容,可以采用传入词袋模型,也可以用词集模型 classList=[1,0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0]
# 训练样本的预分类 return wordList,classList def creatVocabList(self,wordList): vocabSet=set([]) for document in wordList: vocabSet=vocabSet|set(document) vocabList=list(vocabSet) return vocabList def setOfWords2Vec(self,vocabList,words): wordVec=[0]*len(vocabList) for word in words: if word in vocabList: wordVec[vocabList.index(word)]=1 return wordVec def bagOfWords2Vec(self,vocabList,words): wordVec=[0]*len(vocabList) for word in words: if word in vocabList: wordVec[vocabList.index(word)]+=1 else: pass return wordVec def trainNB(self,vocabList,trainMat,classList): numWords=len(vocabList) pSpam=(sum(classList)+1)/(len(classList)+2) p1Num=np.ones(numWords) p0Num=np.ones(numWords) p1Denom=0 p0Denom=0 for i in range(len(classList)): if classList[i]==1: p1Num+=trainMat[i] p1Denom+=sum(trainMat[i]) else: p0Num+=trainMat[i] p0Denom+=sum(trainMat[i]) p1Denom+=numWords p0Denom+=numWords p1Vec=np.log(p1Num/p1Denom) p0Vec=np.log(p0Num/p0Denom) return p1Vec,p0Vec,pSpam def classifyNB(self,vocabList,trainMat,newWordVec,classList): p1Vec,p0Vec,pSpam=self.trainNB(vocabList,trainMat,classList) p1=sum(newWordVec*p1Vec)+np.log(pSpam) p0=sum(newWordVec*p0Vec)+np.log(1-pSpam) return True if p1>p0 else False def runTest(self): wordList,classList=self.loadData() vocabList=self.creatVocabList(wordList) trainMat=[] for words in wordList: trainMat.append(self.setOfWords2Vec(vocabList,words)) testWords=jieba.cut(self.testWords) newWordVec=self.setOfWords2Vec(vocabList,testWords) result=self.classifyNB(vocabList,trainMat,newWordVec,classList) return True if result else False # testWords=‘你真丑,我讨厌你‘ # result=isgentry(testWords).runTest() # 返回布尔值,真为粗鲁语言
优点:
(1)算法逻辑简单,易于实现(算法思路很简单,只要使用贝叶斯公式转化即可!)
(2)分类过程中时空开销小(假设特征相互独立,只会涉及到二维存储)
缺点:
理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。
而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
伯努利朴素贝叶斯:BernoulliNB 重复的词语视为只出现一次
多项式朴素贝叶斯:MultinomialNB 重复的词语视为出现多次
高斯朴素贝叶斯: GaussianNB 特征属性是连续数值
希望对正在入门机器学习的同学有帮助~
标签:现象 为什么 art 通过 http 布尔值 存储 就是 cab
原文地址:https://www.cnblogs.com/songyifan427/p/11609834.html