标签:target 倒数 描述 == length tps 条件 ima 解析
给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
注意:
答案中不可以包含重复的四元组。
示例:
给定数组 nums = [1, 0, -1, 0, -2, 2],和 target = 0。
满足要求的四元组集合为:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]
四数之和和三数之和求解思路一毛一样。三数之和解析:https://www.cnblogs.com/MrSaver/p/5913336.html
首先数组进行有序话,接着我们固定a和b,在ab固定的情况下,cd分别向内考虑,调整四数之和。
当c和d把所有情况都遍历完后,b向右移动一格并固定,cd分别向内考虑,调整四数之和。
当b移动到倒数第三位时,b的所有情况就算遍历玩了,最后a向右移动一格并固定。
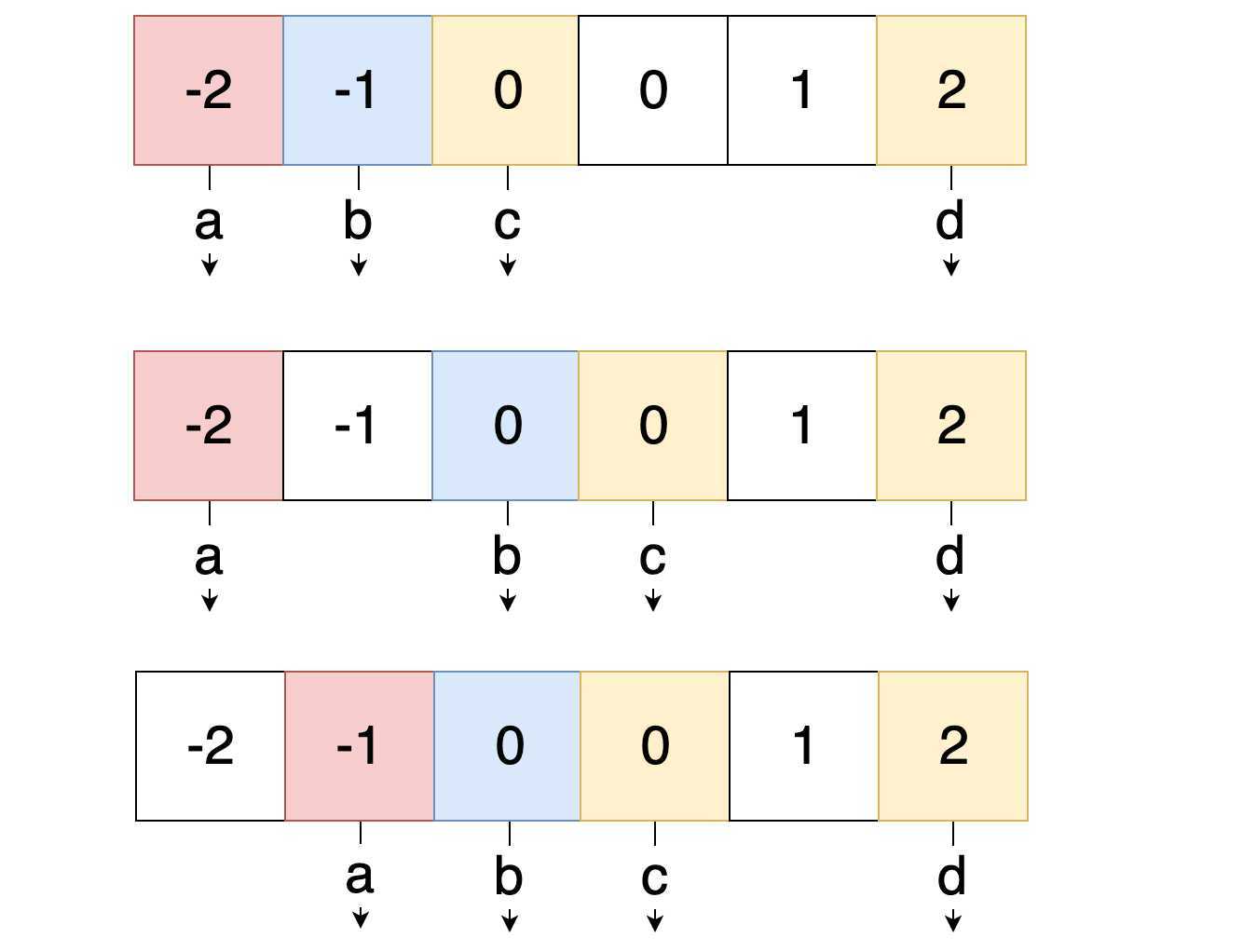
我们知道用双指针模型解决问题,就要将N数之和的前N-2项进行固定,通过移动N项和N-1项来匹配目标值,即五数之和就需要将a,b,c固定,移动d、e。
所谓固定不是不移动,他们仍然需要进行暴力的遍历操作,只是在双指针移动完后再动。
这道题还是很值得思考的!
public class Solution {
public static List<List<Integer>> fourSum(int[] nums, int target) {
//[!]这里引入map用来去重
Map<String,Boolean> map = new HashMap<>();
List<List<Integer>> result = new ArrayList<>();
//[!]数组长度小于4直接返回空
if(nums.length < 4) return result;
//[!]做排序以便使用双指针模型
Arrays.sort(nums);
int a = 0;
while(a < nums.length - 3) {
int b = a + 1;
while (b<nums.length-2){
int c = b + 1;
int d = nums.length-1;
while(c < d) {
int sum = nums[a] + nums[b] + nums[c]+nums[d];
if(sum == target) {
if(!map.containsKey(nums[a]+"|"+nums[b]+"|"+nums[c]+"|"+nums[d]))
{
map.put(nums[a]+"|"+nums[b]+"|"+nums[c]+"|"+nums[d],true);
result.add(Arrays.asList(nums[a], nums[b], nums[c],nums[d]));
}
}
//[!]一直递增C,直到和等于或大于目标值
if(sum <= target) while(nums[c] == nums[++c] && c < d);
//[!]当值大于目标值时,开始递减D,等于时判断使d跳过重复值
if(sum >= target) while(nums[d--] == nums[d] && c < d);
}
b++;
}
a++;
}
return result;
}
public static void main(String[] args) {
int[] nums = {1,0,-1,0,-2,2};
fourSum(nums,0);
}
}
标签:target 倒数 描述 == length tps 条件 ima 解析
原文地址:https://www.cnblogs.com/MrSaver/p/11613102.html