树-二叉树的基本概念

标签：inf   完全   编号   mic   play   image   证明   isp   大于   

二叉树的特点

• 每个结点至多有二棵子树(即不存在度大于2的结点)
• 二叉树的子树有左、右之分，且其次序不能任意颠倒

卡特兰数

具有n个结点的不同形态的二叉树数目，即所谓的n阶卡特兰数。（也是含有n个结点的栈的出队顺序的总情况）

二叉树的性质（约定空二叉树的高度为-1）

• 高度为h>=0的二叉树至少有h+1个结点。
• 高度为h>=0的二叉树至多有2^h+1-1个结点
• 含有n>=1个结点的二叉树的高度至多为n-1
• 含有n>=1个结点的二叉树的高度至少为[log₂n](向下取整)
• 对于任何一棵二叉树，如果其叶节点的数目为n₀，度为2的结点数目为n₂,则n₀=n₂+1

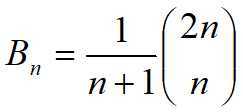
证明：设n₁为二叉树中度为1的结点数目，故结点总数为n=n₀+n₁+n₂.

　　　在二叉树中，除根结点外，每个结点都有一条分支进入，设B为分支总数，则n=B+1.

　　　又因为分支有度为1和度为2的结点射出，B=n₁+2n₂

　　　于是n=n₁+2n₂+1=n₀+n₁+n₂，得到n₀=n₂+1

满二叉树

•  定义：一棵高度为h且有2^h+1-1个结点的二叉树称为满二叉树

完全二叉树

• 定义：若一棵二叉树最多只有最下面的2层上结点的度数可以小于2，并且最下面一层上的节点都集中在该层的最左边，则这种二叉树称为近似满二叉树
• 性质：如果对一棵有n个结点的完全二叉树的结点按层序编号，则对任一结点i(1<=i<=n)，有

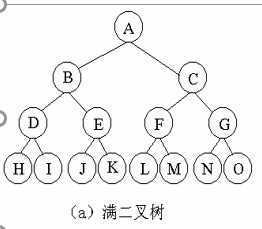
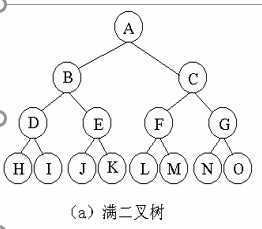
  　　　　(1)  如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲是[i/2]（向下取整）

 　　　　 (2)  如果2i>n，则结点i无左孩子；如果2i<=n，则其左孩子是2i

  　　　　(3)  如果2i+1>n，则结点i无右孩子；如果2i+1<=n，则其右孩子是2i+1

• 例题：一棵完全二叉树有1001个结点，其中叶节点的个数是（501）

　　　　解：最后一个分支结点的序号为[1001/2]=500,故叶子节点的个数为501

树-二叉树的基本概念

标签：inf   完全   编号   mic   play   image   证明   isp   大于   

原文地址：https://www.cnblogs.com/KBryant/p/11613664.html