标签：图片   lib   积分   微积分   一个   技术   长度   com   随机   

Q1-1：一段1米长的绳子 随机切两刀 分成三段 求能够组合成一个三角形的概率

不妨设x为两个切点坐标中的较小值，y为较大值，x≠y

可能情况的全体为：

可能情况全体构成的区域为：

三角形三边关系：

三条边的长度分别为：x, y-x, 1-y

则：x+y-x>1-y

y-x+1-y>x

1-y+x>y-x

整理得：

y>0.5

x<0.5

y-x<0.5

该事件的可行域是：

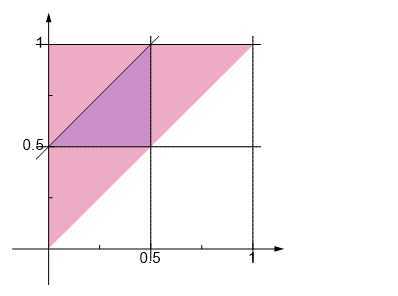
因此，能组成三角形的概率是0.25

解法二：设切下来的两段长度分别为x，y

事件全体构成的区域表示为：

x>0且

y>0且

1-x-y>0

三角形三边关系：

x+y>1-x-y

y+1-x-y>x

1-x-y+x>y

如图：

解法三：微积分法

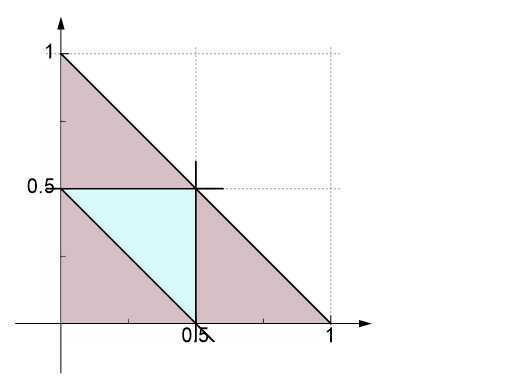
分情况讨论：

1. 0<x<y<1
2. 0<y<x<1

若x<y，则根据三边关系，有：

x<0.5

y>0.5

y-x<0.5

若x>y，则根据三边关系，有

x>0.5

y<0.5

x-y<0.5

以情况一为例：

x服从[0, 0.5]上的均匀分布

y的取值满足条件0.5<y<0.5+x

取积分：

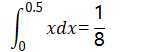
乘以2，得0.25

对微积分法的解释：

第一步：在[0, 1]上投掷点x，假设x落点是随机的，概率就是1

第二步：x落点确定之后，随机投掷y

y的可能取值也是[0, 1]

第三步：x分情况讨论，x<0.5 + x>0.5

1. x<0.5：

满足条件的y的区间是[0.5, x+0.5]（根据三角形三边关系确定的）

该区间长度为x，点y落在该区间内的概率是x/1 = x

2. x>0.5：同理

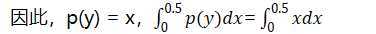
注意：假设线段长度为10，则应用上述微积分表达式时，注意使用雅可比系数（1/10）

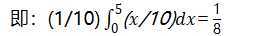
2019年9月30日  于南湖湖畔  

机器学习 – 练习题

标签：图片   lib   积分   微积分   一个   技术   长度   com   随机   

原文地址：https://www.cnblogs.com/sddai/p/11614181.html