标签：逆序 add 初始化 今天 矩阵快速幂 数据结构 覆盖 矩阵 sum
刚刚写了一个小时的博客没了，浏览器自动刷新。
一！个！小！时！
鼠标键盘电脑哪个都不能摔，气死我了。
垃圾选手T1T2没思路，T3倒是想出来得比较早，靠T3撑着分数。
数据结构学傻选手，属实垃圾。
T1平均数：
一个序列的所有数如果减去x，那么平均数也会减去x。可以二分这个x，统计序列里平均数小于0的序列的个数，含义为原序列平均数小于x的序列的个数。最后统计值小于k且最接近k的x就是所求答案。
序列的平均数小于0，那么序列的和也一定小于0。表现在前缀和上即为一个区间的sumr<suml-1，转化为求前缀和序列的逆序对个数。
归并排序的时候前缀和数组下标从0开始，因为可能存在序列开始的一段就小于0的情况，要和sum0比较。
#include<iostream> #include<cstdio> using namespace std; int n,k; double ans; int num; double b[100010],c[100010],s[100010],a[100010],maxx; void work(int l,int r){ if(l==r){ b[l]=s[l]; return; } int mid=(l+r)/2; work(l,mid); work(mid+1,r); int ll=l,rr=mid+1,p=l; while(ll<=mid&&rr<=r){ if(b[ll]<=b[rr]){ c[p++]=b[ll++]; } else{ num+=mid-ll+1; c[p++]=b[rr++]; } } while(ll<=mid){ // num+=r-mid; c[p++]=b[ll++]; } while(rr<=r){ c[p++]=b[rr++]; } for(int i=l;i<=r;i++){ b[i]=c[i]; } } int check(double x){ num=0; for(int i=1;i<=n;i++){ s[i]=s[i-1]+a[i]-x; } work(0,n); return num; } int main(){ scanf("%d%d",&n,&k); for(int i=1;i<=n;i++){ scanf("%lf",&a[i]); maxx=max(maxx,a[i]); } double l=0,r=1e9; while(l+1e-5<r){ double mid=(l+r)*0.5; if(check(mid)<k){ l=mid; } else r=mid; } printf("%.4lf",l); return 0; }
T2涂色游戏：
考试的时候先想到矩阵快速幂，然后不会推DP式子……
因为相邻两列涂q种颜色与具体是哪种颜色无关，转化成关于列的DP问题。
先求出一列涂i种颜色的方案数。设f[i][j]为一列里到第i行涂了j种颜色的方案数，f[i][j]=f[i-1][j-1]*(p-(j-1))+f[i-1][j]*j，含义是从剩下的p-(j-1)种颜色中选一个新颜色涂，或者从已有的j种颜色中选一个重复。设g[i]=f[n][i]，g[i]即一列涂i种颜色的方案数。
考虑从上一列的j种颜色转移到这一列的k种颜色。对于每一种确定的用了j种颜色的涂色方案，先枚举j和k的并集x。那么这种情况下k可以分成两部分，与j交集的部分有C(j,j+k-x)种选择，k剩下的颜色有C(p-j,x-j)种选择。然后对于每一种确定了k种颜色的选择方案，有g[k]/C(p,k)种涂色方案。
那么每一种确定的j转移给k的方案数就是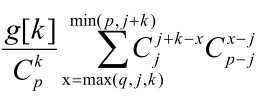
，再乘上一个dp[i-1][j]，即上一列j种颜色的总方案数。
初始化是dp[1][i]=g[i]。
发现对于不同列的j到k的转移，乘上的参数是一样的，那么就可以用矩阵快速幂优化。
答案矩阵的初始化是dp[1][i]，转移矩阵的a[i][j]即为i转移到j的参数，然后进行矩阵快速幂m-1次（从第二列开始）。
#include<iostream> #include<cstdio> using namespace std; const int mod=998244353; int n,m,p,q; long long f[110][110],c[110][110],dp[1010][110],ans; struct node{ long long g[110][110]; }a,b,d; long long ks(long long x,long long k){ long long num=1; while(k){ if(k&1)num=num*x%mod; x=x*x%mod; k>>=1; } return num; } long long cal(int j,int k){ long long num=0; for(int x=max(q,max(j,k));x<=min(p,j+k);x++){ num=(num+(c[j][j+k-x]*c[p-j][x-j]%mod)%mod)%mod; } return num; } node cheng(node x,node y){ node e; for(int i=1;i<=p;i++){ for(int j=1;j<=p;j++){ e.g[i][j]=0; } } for(int k=1;k<=p;k++){ for(int i=1;i<=p;i++){ for(int j=1;j<=p;j++){ e.g[i][j]=(e.g[i][j]+x.g[i][k]*y.g[k][j]%mod)%mod; } } } return e; } void ksm(int k,node x){ while(k){ if(k&1)b=cheng(b,x); x=cheng(x,x); k>>=1; } } int main() { scanf("%d%d%d%d",&n,&m,&p,&q); c[0][0]=1; for(int i=1;i<=100;i++){ c[i][0]=1; for(int j=1;j<=i;j++){ c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod; } } f[0][0]=1; for(int i=1;i<=n;i++){ for(int j=1;j<=p;j++){ f[i][j]=(f[i-1][j]*j%mod+f[i-1][j-1]*(p-(j-1))%mod)%mod; } } for(int i=1;i<=p;i++){ for(int j=max(q-i,1);j<=min(n,p);j++){ a.g[i][j]=(a.g[i][j]+f[n][j]*ks(c[p][j],mod-2)%mod*cal(i,j)%mod)%mod; } } for(int i=1;i<=p;i++){ b.g[1][i]=f[n][i]; } m--; ksm(m,a); for(int i=1;i<=p;i++){ ans=(ans+b.g[1][i])%mod; } printf("%lld",ans); return 0; }
T3序列：
一边写题解一边复习这些题才搞了一个多小时，第二遍写倒是挺快的。然后T3可能将是今天写题解耗时最少的题……？
看到强制在线，第一反应是答案由上一个答案转移而来。
n和q的复杂度都是1e5级别，肯定要优化其中一个到log。因为答案很可能从上一个进行变化而来，每次修改是单点的，询问的具体内容又不变，考虑怎么才能存下询问的全部信息并快速找出每次修改影响了哪些询问。
询问是区间询问的形式，考虑存下哪个询问的x覆盖了哪些范围，并快速得知每次修改的位置会影响哪些x。发现对于每次修改，覆盖了修改位置的x中，受到影响的x在一定范围内，即修改位置的原数与现在的数的中间这个范围。因为每次只修改一个位置，对于一个询问若存在影响只能是答案+1或-1，所以如果能够快速查出多少个x在这个受到影响的范围内就能得知答案进行了多少变化。于是把询问的左右端点拆开，像差分一样，l处记录x的+1，r+1处记录x的-1。然后用一棵下标是x的值的主席树，保存序列每个位置受到哪些x的覆盖。
对于每次修改，只要查出修改位置有多少个x的值在修改值和原值中间而受到影响，对答案进行相应加减即可。
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; int n,m,q,cnt1,pre=1; int a[100010],tree[100010]; long long ans; struct node{ int pos,x,val; }b[200010]; struct node1{ int l,r,x; }c[200010]; bool cmp(node x,node y){ if(x.pos<y.pos)return true; else return false; } int T[300010*18],L[300010*18],R[300010*18],tot,cnt[300010*18]; void build(int &p,int l,int r){ p=++tot; if(l==r)return; int mid=(l+r)/2; build(L[p],l,mid); build(R[p],mid+1,r); } void update(int &p,int pre,int l,int r,int x,int val){ p=++tot; L[p]=L[pre],R[p]=R[pre],cnt[p]=cnt[pre]+val; if(l==r)return; int mid=(l+r)/2; if(x<=mid)update(L[p],L[pre],l,mid,x,val); else update(R[p],R[pre],mid+1,r,x,val); } void add(int x){ for(;x<=n;x+=(x&-x))tree[x]++; } int ask(int x){ if(!x)return 0; int val=0; for(;x;x-=(x&-x))val+=tree[x]; return val; } int query(int p,int l1,int r1,int l,int r){ if(l1<=l&&r<=r1)return cnt[p]; int mid=(l+r)/2; if(r1<=mid)return query(L[p],l1,r1,l,mid); if(l1>mid)return query(R[p],l1,r1,mid+1,r); return query(L[p],l1,mid,l,mid)+query(R[p],mid+1,r1,mid+1,r); } int main() { scanf("%d%d%d",&n,&m,&q); for(int i=1;i<=n;i++){ scanf("%d",&a[i]); } for(int i=1,x,y,z;i<=m;i++){ scanf("%d%d%d",&x,&y,&z); b[++cnt1].pos=x,b[cnt1].x=z,b[cnt1].val=1; b[++cnt1].pos=y+1,b[cnt1].x=z,b[cnt1].val=-1; c[i].l=x,c[i].r=y,c[i].x=z; } sort(b+1,b+2*m+1,cmp); cnt1=1; build(T[0],1,n); for(int i=1;i<=n+1;i++){ if(b[cnt1].pos==i){ while(b[cnt1].pos==i){ update(T[i],pre,1,n,b[cnt1].x,b[cnt1].val); pre=T[i]; if(b[cnt1].val==-1){//r ans+=ask(n)-ask(b[cnt1].x-1); } else{//l ans-=ask(n)-ask(b[cnt1].x-1); } cnt1++; } } else if(i<=n){ T[i]=pre; } if(i<=n)add(a[i]); } printf("%lld\n",ans); for(int i=1,p,v;i<=q;i++){ scanf("%d%d",&p,&v); long long pos=p^ans; long long x=v^ans; if(x>a[pos]){ int num=query(T[pos],a[pos]+1,x,1,n); ans+=num; a[pos]=x; } else if(x<a[pos]){ int num=query(T[pos],x+1,a[pos],1,n); ans-=num; a[pos]=x; } printf("%lld\n",ans); } return 0; }
再也不用垃圾浏览器写题解了orzzzzzzzz气死我了
一晚上就写这一篇了，虽然连带了漫长的复习时间，重新搞懂这些题并努力总结套路…
咕掉的题解还有n篇，我好难——
标签：逆序 add 初始化 今天 矩阵快速幂 数据结构 覆盖 矩阵 sum
原文地址：https://www.cnblogs.com/chloris/p/11614198.html
