标签:每日 最大 inline mic com line ima style 如图所示
在等腰\(\triangle ABC\)中,角\(A,B,C\)所对的边分别为\(a,b,c\),其中\(B\)为钝角,且\(b-\)\(\sqrt{3}a\sin A\)\(=b\)\(\cos 2A\),点\(D\)与点\(B\)在直线\(AC\)的两侧,且\(CD=3AD=3\),则\(\triangle BCD\)的面积的最大值是\((\qquad)\)
\(\mathrm{A}.\dfrac{3}{4}\sqrt{3}\qquad\) \(\mathrm{B}.4\sqrt{3}\qquad\) \(\mathrm{C}.\dfrac{5}{4}\sqrt{3}\qquad\) \(\mathrm{D}.3\)
解析: 由题中所给条件等式可得\[
\begin{split}
\sin B-\sqrt{3}\sin^2 A&=\sin B\cos 2A \\ &=\sin B-2\sin B \sin^2A.
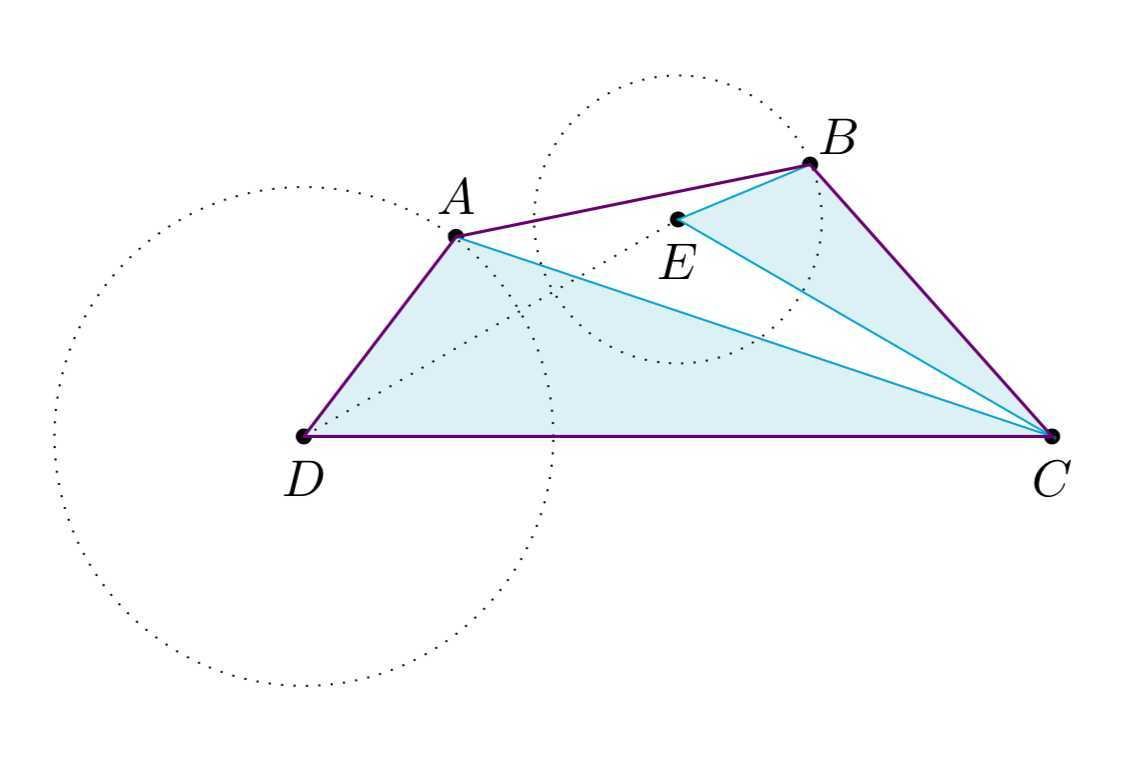
\end{split}\]所以\(\sin B=\dfrac{\sqrt{3}}{2}\),又因为\(B\)为钝角,所以\[B=\dfrac{2\pi}{3}.\]固定\(DC\)边,则\(A\)点在以\(D\)为圆心,以\(1\)为半径的圆上运动,如图所示
标签:每日 最大 inline mic com line ima style 如图所示
原文地址:https://www.cnblogs.com/Math521/p/11614450.html