标签:ndis 运行 绝对值 win 要求 执行 发表 时间 set
二叉搜索树只有保持平衡时其查找效率才会高。
要保持二叉搜索树的平衡不是一件易事。不过还是有一些非常经典的办法可以做到,其中最好的方法就是将二叉搜索树实现为AVL树。
AVL树得名于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis,他们在 1962 年的论文 "An algorithm for the organization of information" 中发表了它。AVL树是一种特殊类型的二叉树,它的每个结点都保存一份额外的信息:结点的平衡因子。
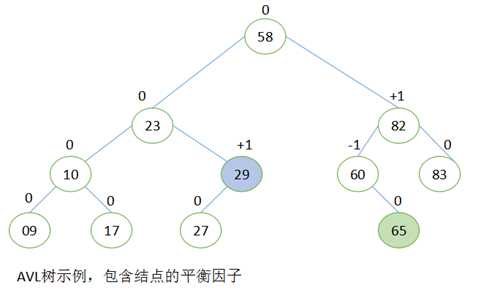
结点的平衡因子 = 左子树的高度 - 右子树的高度
插入和删除操作都会导致AVL树的自我调整(自我平衡),使得所有结点的平衡因子保持为+1、-1或0。
当子树的根结点的平衡因子为+1时,它是左倾斜的(left-heavy)。
当子树的根结点的平衡因子为 -1时,它是右倾斜的(right-heavy)。
一颗子树的根结点的平衡因子就代表该子树的平衡性。
保持所有子树几乎都处于平衡状态,AVL树在总体上就能够基本保持平衡。
AVL树的基本查找、插入结点的操作和二叉树的操作一样。但是,当向AVL树中插入一个结点后,还有一些额外的工作要做。首先,必须计算因插入操作对平衡因子带来的改变。其次,如果任何平衡因子变成了+/-2,就必须从这个结点开始往下重新平衡这颗树,这个重新平衡的过程就称为旋转。
旋转操作用来重新平衡树的某个部分。通过重新安排结点 ,使结点之间的关系始终保持左子结点小于父结点,父结点小于右子结点。使得该树仍然是一颗二叉搜索树。旋转过后,旋转子树中的所有结点的平衡因子都为+1、-1或0。
AVL树的旋转类型有4种, 分别是LL(left-left)旋转、LR(left-right)旋转、RR(right-right)旋转和RL(right-left)旋转。
为方便理解在何时执行哪一种旋转,设x代表刚插入AVL树中的结点,设A为离x最近且平衡因子更改为2的绝对值的祖先。可以归纳为下面4种处理情况:
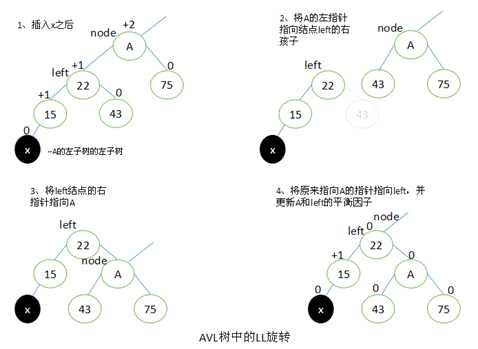
如下图所示,当x位于A的左子树的左子树上时,执行LL旋转。
设left为A的左子树,要执行LL旋转,将A的左指针指向left的右子结点,left的右指针指向A,将原来指向A的指针指向left。
旋转过后,将A和left的平衡因子都改为0。所有其他结点的平衡因子没有发生变化。
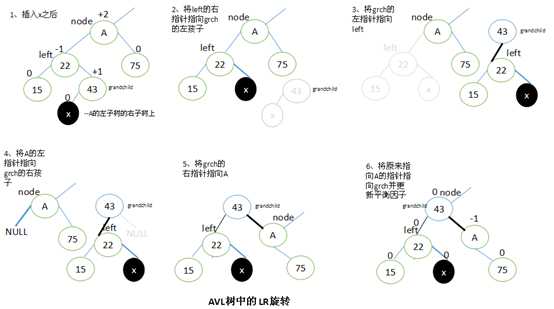
当x位于A的左子树的右子树上时,执行LR旋转。
设left是A的左子结点,并设A的子孙结点grandchild为left的右子结点。
要执行LR旋转,将left的右子结点指向grandchild的左子结点,grandchild的左子结点指向left,A的左子结点指向grandchild的右子结点,再将grandchild的右子结点指向A,最后将原来指向A的指针指向grandchild。
执行LR旋转之后,调整结点的平衡因子取决于旋转前grandchild结点的原平衡因子值。
如果grandchild结点的原始平衡因子为+1,就将A的平衡因子设为-1,将left的平衡因子设为0。
如果grandchild结点的原始平衡因子为0,就将A和left的平衡因子都设置为0。
如果grandchild结点的原始平衡因子为-1,就将A的平衡因子设置为0,将left的平衡因子设置为+1。
在所有的情况下,grandchild的新平衡因子都是0。所有其他结点的平衡因子都没有改变。
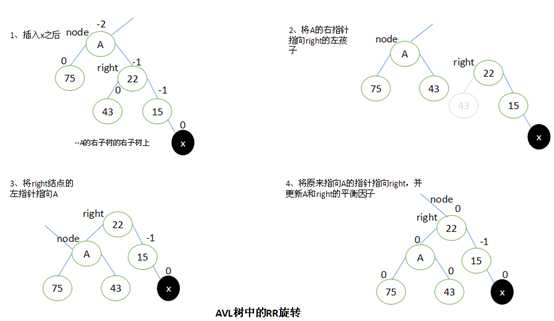
当x位于A的左子树的右子树上时,执行RR旋转。
RR旋转与LL旋转是对称的关系。
设A的右子结点为Right。要执行RR旋转,将A的右指针指向right的左子结点,right的左指针指向A,原来指向A的指针修改为指向right。
完成旋转以后,将A和left的平衡因子都修改为0。所有其他结点的平衡因子都没有改变。
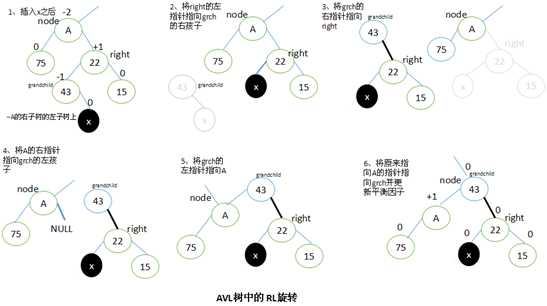
当x位于A的右子树的左子树上时,执行RL旋转。
RL旋转与LR旋转是对称的关系。
设A的右子结点为right,right的左子结点为grandchild。要执行RL旋转,将right结点的左子结点指向grandchild的右子结点,将grandchild的右子结点指向right,将A的右子结点指向grandchild的左子结点,将grandchild的左子结点指向A,最后将原来指向A的指针指向grandchild。
执行RL旋转以后,调整结点的平衡因子取决于旋转前grandchild结点的原平衡因子。这里也有三种情况需要考虑:
如果grandchild的原始平衡因子值为+1,将A的平衡因子更新为0,right的更新为-1;
如果grandchild的原始平衡因子值为 0,将A和right的平衡因子都更新为0;
如果grandchild的原始平衡因子值为-1,将A的平衡因子更新为+1,right的更新为0;
在所有情况中,都将grandchild的新平衡因子设置为0。所有其他结点的平衡因子不发生改变。
红黑树是一种自动平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。它是复杂的,但它的操作有着良好的最坏情况运行时间,并且在实践中是高效的:它可以在O(logn)时间内查找、插入和删除,这里的n是树中元素的数目。
红黑树是2-3-4树的一种等同。换句话说,对于每个2-3-4树,都存在至少一个元素是同等次序的红黑树。在2-3-4树上的插入和删除操作也等同于在红黑树中颜色翻转和旋转。这使得2-3-4树成为理解红黑树背后的逻辑的重要工具。
红黑树相对于AVL树来说,牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作,整体来说性能要优于AVL树。
性质
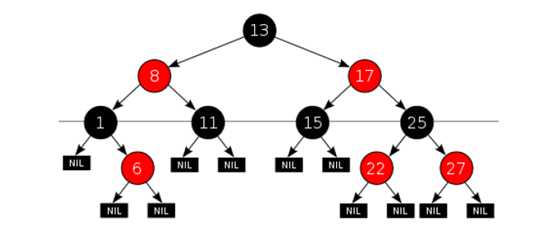
(1)节点非红即黑
(2)根节点时黑色的
(3)每个叶子节点(NULL节点)是黑色的
(4)每个红色节点的两个子节点都是黑色的(不能有两连续的红色节点)
(5)从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
注意:性质(5)保证红黑树的最长路径不超过最短路径的两倍
(1)简介
AVL树是带有平衡条件的二叉查找树,一般通过平衡因子差值判断是否平衡并通过旋转来实现平衡,左右子树高不超过1,和红黑树相比,AVL树是严格的平衡二叉树,平衡条件必须满足(所有节点的左右子树高度差不超过1)。不管我们是执行插入还是删除操作,只要不满足上面的条件,就要通过旋转来保持平衡,而因为旋转非常耗时,由此我们可以知道AVL树适合用于插入与删除次数比较少,但查找多的情况。
(2)局限性
由于维护这种高度平衡所付出的代价比从中获得的效率收益还大,故而实际的应用不多,更多的地方是用追求局部而不是非常严格整体平衡的红黑树。当然,如果应用场景中对插入删除不频繁,只是对查找要求较高,那么AVL还是较优于红黑树。
(3)应用
1.Windows NI内核中广泛存在;
(1)简介
一种二叉查找树,但在每个节点增加一个存储位表示结点的颜色,可以是红或黑(非红即黑)。通过对任何一条从根到叶子的路径上各个节点着色的方法的限制,红黑树确保没有一条路会比其他路径长出两倍,因此红黑树是一种弱平衡二叉树(由于是弱平衡,可以看到,在相同的节点情况下,AVL树的高度低于红黑树),相对于要求严格的AVL树来说,它的旋转次数少,插入最多两次旋转,删除最多三次旋转,所以对于搜索、插入、删除操作比较多的情况下,我们就用红黑树。
(2)性质
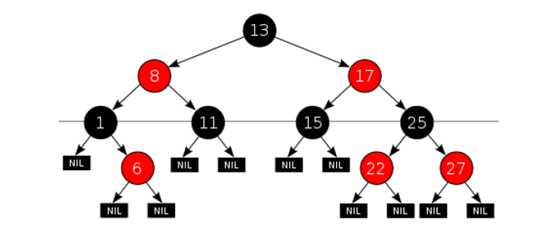
(1)节点非红即黑
(2)根节点时黑色的
(3)每个叶子节点(NULL节点)是黑色的
(4)每个红色节点的两个子节点都是黑色的(不能有两连续的红色节点)
(5)从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
注意:性质(5)保证红黑树的最长路径不超过最短路径的两倍
(3)应用
广泛应用于C++的STL中,map和set底层都是用红黑树实现的。
标签:ndis 运行 绝对值 win 要求 执行 发表 时间 set
原文地址:https://www.cnblogs.com/kexinxin/p/11618273.html