标签:top uniq 问题 ror scanf 个数 oss 高度 字符串
给定一个长度为 \(n\) 的序列 \(a\) ,定义 \((x,y)\) "可到达" 为:可以选出若干个位置 \(p_1...p_k\) ,使得 \(\forall x\le p_i \le y\) \(\forall a_{p_i}\&a_{p_{i+1}}\not=0\) , \(q\) 次询问 \((x,y)\) 是不是 "可到达" 的
\(n,q,a_i\le 3\times 10^5\)
tags : dp , bitmarks
原操作等价于从第 \(x+1\) 开始枚举到 \(y-1\) ,一路上遇到一个数按位与不是 \(0\) 就或起来。
可以线段树加速这个过程,线段树每个节点上有 \(\log({\max})\) 个数字,每一位顺次表示扔一个 \(2^k\) 进去之后出来的答案,时间复杂度 \(O(q\log^2n)\)
#include <bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int a[N];
struct Node{
int val[20];
}tree[N<<2];
inline void pushup(int root){
for (int i=0;i<19;i++){
tree[root].val[i]=tree[root<<1].val[i];
int v=tree[root<<1].val[i];
for (int j=0;j<19;j++)
if ((1<<j)&v) tree[root].val[i]|=tree[(root<<1)|1].val[j];
tree[root].val[i]|=tree[(root<<1)|1].val[i];
}
}
#define mid ((l+r)>>1)
inline void build(int root,int l,int r){
if (l==r){
for (int i=0;i<19;i++)
if (a[l]&(1<<i)) tree[root].val[i]=a[l];
return;
}
build(root<<1,l,mid);
build((root<<1)|1,mid+1,r);
pushup(root);
}
int v;
inline void query(int root,int l,int r,int L,int R){
if (r<L||l>R) return;
if (L<=l&&r<=R){
int x=0;
for (int i=0;i<19;i++)
if (v&(1<<i)) x|=tree[root].val[i];
v|=x;
return;
}
query(root<<1,l,mid,L,R);
query((root<<1)|1,mid+1,r,L,R);
}
int main (){
int n,q;scanf ("%d%d",&n,&q);
for (int i=1;i<=n;i++) scanf ("%d",&a[i]);
build(1,1,n);
while (q--){
int x,y;scanf ("%d%d",&x,&y);
if (x+1==y) {puts((a[x]&a[y])?"Shi":"Fou");continue;}
v=a[x];query(1,1,n,x+1,y-1);
if (v&a[y]) puts("Shi");
else puts("Fou");
}
return 0;
}
给定 \(n\) 个数字的集合,每次可以取出一个数字,设当前取出的是 \(x\) ,上一个取出的是 \(y\)
求获胜概率,对 \(998244353\) 取模
\(n\le 5\times 10^3\)
tags : dp , math , probabilities
获胜条件是先取出一个单调上升序列,然后再取出一个和末尾元素相等的数字
\(f[i][j]\) 表示当前选择了 \(i\) 个数字,最后一个数字为第 \(j\) 个的概率
\(f[i][j]=\sum_{k=0}^{j-1}f[i-1][k]\times \frac{cnt[j]}{n-i+1}=\frac{cnt[j]}{n-i+1}\times \sum_{k=0}^{j-1}f[i-1][k]\)
可以前缀和优化,答案很容易计算
#include <bits/stdc++.h>
using namespace std;
const int N=5005,Mod=998244353;
int dp[N][N],sum[N][N],a[N],inv[N];
inline int qpow(int a,int b){
int ans=1;
while (b){
if (b&1) ans=1ll*ans*a%Mod;
a=1ll*a*a%Mod,b>>=1;
}
return ans;
}
int cnt[N];
int main (){
int n;scanf ("%d",&n);
for (int i=1;i<=n;i++) scanf ("%d",&a[i]),cnt[a[i]]++,inv[i]=qpow(i,Mod-2);
sort(a+1,a+n+1);
dp[0][0]=1;
int ans=0,sum;
for (int i=1;i<=n;i++){
if (i==1) sum=1;else sum=0;
for (int j=1;j<=n;j++){
if (a[j]==a[j-1]){
ans=(ans+1ll*dp[i-1][j-1]*(cnt[a[j]]-1)%Mod*inv[n-i+1]%Mod)%Mod;
continue;
}
dp[i][j]=1ll*sum*cnt[a[j]]%Mod*inv[n-i+1]%Mod;
sum=(sum+dp[i-1][j])%Mod;
}
}
printf ("%d",ans);
return 0;
}
考虑一种更为自然的做法:
\(f[i][j]\) 表示前 \(i\) 个数字选了 \(j\) 个的概率
\(f[i][j]=f[i-1][j]+f[i-1][j-1]\times \frac{cnt[i]}{n-j+1}\)
计算答案考虑选两个当前数字即可
给定 \(n\) ,问 \(1\dots n\) 的所有排列中,对于一个排列设前缀 \(\gcd\) 的不同个数为 \(x_i\) ,问有多少个排列的前缀 \(\gcd\) 不同个数达到 \(\max(x_i)\) ,个数对 \(10^9+7\) 取模。
\(n\le 10^6\)
tags : combinatorics , dp , math , number theory
考虑排列的第一个数 。假如分解质因子后为 \(\prod p_i^{c_i}\),那么此时排列价值的最大值为 \(\sum c_i\)。
所以不同个数达到 \(\max\) ,\(\sum c_i\) 一定要达到 \(\max\) ,容易发现 \(\ge 5\) 的质因子不可能存在,因为 \(2^2<5\) ,而至多存在一个 \(3\) ,因为 \(2^3<3^2\)
设 \(dp[i][j][k]\) 表示前 \(i\) 个数字,当前 \(\gcd\) 有 \(j\) 个因子 \(2\) ,有 \(k\) 个因子 \(3\) ,显然 \(0\le j\le \log_2{n}\) , \(0\le k\le 1\)
考虑转移,如果一次减少了两个因子,那么价值一定不再是最大,所以一次至多减少一个因子
( \(cnt(x)\) 表示 \([1,n]\) 中 \(x\) 的倍数的个数,即 \(\lfloor \frac{n}{x}\rfloor\) )
最后看一下初始化,\(f[1][\lfloor \log_2{n}\rfloor][0]=1\) 是必须的,如果满足可以取 \(3\) 而无法取两个 \(2\) 的话,\(3\) 处也要初始化
时间复杂度 \(O(n\log n)\)
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5,Mod=1e9+7;
int n,dp[N][25][2];
inline int cnt(int x){
return n/x;
}
int main (){
scanf ("%d",&n);
dp[1][(int)(log2(n))][0]=1;
if ((1<<((int)(log2(n))-1))*3<=n) dp[1][(int)(log2(n))-1][1]=1;
for (int i=2;i<=n;i++)
for (int j=0;j<=(int)(log2(n));j++){
dp[i][j][0]=(1ll*dp[i-1][j][0]*(cnt(1<<j)-(i-1))+
1ll*dp[i-1][j+1][0]*(cnt(1<<j)-cnt(1<<(j+1)))+
1ll*dp[i-1][j][1]*(cnt(1<<j)-cnt((1<<j)*3)))%Mod;
dp[i][j][1]=(1ll*dp[i-1][j][1]*(cnt((1<<j)*3)-(i-1))+
1ll*dp[i-1][j+1][1]*(cnt((1<<j)*3)-cnt((1<<(j+1))*3)))%Mod;
}
printf ("%d",dp[n][0][0]);
return 0;
}给定一个长度为 \(n\) 的数列 \(a\) ,\(a\) 由 \(-1\) 和 \([1,k]\) 之内的数字组成,\(-1\) 表示可以填入任意一个 \([1,k]\) 之内的数字,问有多少种方案使得最后的数列中没有长度 \(\ge len\) 的相同连续段
\(n\le 10^5,k\le 100\)
tags : dp
设 \(dp[i][j]\) 表示第 \(i\) 个位置,数值为 \(j\) 的方案数
没有限制的转移: \(dp[i][j]=\sum_{s=1}^kdp[i-1][s]\) ,前缀和优化 \(sum[i]=\sum_{j=1}^kdp[i][j]\)
有限制之后,考虑不论多长的连续段,都在长度恰好达到 \(len\) 时扣掉
那么当 \([i-len,i]\) 均可以填 \(j\) 的时候容斥掉方案数,即为 \(dp[i][j]-=sum[i-len]-dp[i-len][j]\)
( 加上 \(dp[i-len][j]\) 是为了加上已经扣过的方案 )
#include <bits/stdc++.h>
using namespace std;
const int N=100005,K=105,Mod=998244353;
int dp[N][K],cnt[N][K],a[N],sum[N];
int main (){
int n,k,len;
scanf("%d%d%d",&n,&k,&len);
for (int i=1;i<=n;i++) scanf ("%d",&a[i]);
for (int j=1;j<=k;j++)
for (int i=1;i<=n;i++){
cnt[i][j]=cnt[i-1][j];
if (a[i]==-1||a[i]==j) cnt[i][j]++;
}
sum[0]=1;
for (int i=1;i<=n;i++){
for (int j=1;j<=k;j++){
if (a[i]==-1||a[i]==j) dp[i][j]=sum[i-1];
if (i>=len&&cnt[i][j]-cnt[i-len][j]==len)
dp[i][j]=((dp[i][j]+dp[i-len][j])%Mod-sum[i-len]+Mod)%Mod;
}
for (int j=1;j<=k;j++) sum[i]=(sum[i]+dp[i][j])%Mod;
}
printf ("%d",sum[n]);
return 0;
}定义 \(f(s,t)\) 为 \(t\) 在 \(s\) 中出现次数
给定一个模式串 \(S\) 和 \(n\) 个匹配串 \(t_i\) ,求 \(\sum_{i=1}^n\sum_{j=1}^nf(S,t_i+t_j)\)
\(n\le 2\times 10^5,|S|\le 2\times 10^5,\sum t_i\le 2\times 10^5\)
tags : brute force , string suffix structures , strings
转化为计算 \(a[i]\) 表示以 \(i\) 结尾的有多少个字符串
相应的,\(b[i]\) 表示以 \(i\) 开头的有多少个字符串
那么答案可以表示为 \(\sum_{i=1}^{|T|-1}a[i]\times b[i+1]\)
问题转化为计算 \(a[i]\) 和 \(b[i]\) ,显然对反串求得的 \(a\) 即为原串的 \(b\) ,所以只考虑计算 \(a[i]\)
\(a\) 数组可以直接在 fail 树上 dp 求得
时间复杂度 \(O(26\times (|S|+|T|)\)
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
struct AC_automaton{
int ch[N][26],fail[N],cnt=0;
int end[N],f[N];
inline void insert(char *s){
int now=0;int l=strlen(s+1);
for (int i=1;i<=l;i++){
if (!ch[now][s[i]-'a']) ch[now][s[i]-'a']=++cnt;
now=ch[now][s[i]-'a'];
}
end[now]++;
}
inline void build(){
queue <int > Q;
for (int i=0;i<26;i++) if (ch[0][i]) Q.push(ch[0][i]);
while (!Q.empty()){
int x=Q.front();Q.pop();
end[x]+=end[fail[x]];
for (int i=0;i<26;i++)
if (ch[x][i]) fail[ch[x][i]]=ch[fail[x]][i],Q.push(ch[x][i]);
else ch[x][i]=ch[fail[x]][i];
}
}
inline void solve(char *s){
int now=0;int l=strlen(s+1);
for (int i=1;i<=l;i++){
now=ch[now][s[i]-'a'];
f[i]=end[now];
}
}
}S1,S2;
char s[N],t[N];
int main (){
scanf ("%s",t+1);
int n;scanf ("%d",&n);
for (int i=1;i<=n;i++){
scanf ("%s",s+1);
S1.insert(s);
int l=strlen(s+1);reverse(s+1,s+l+1);
S2.insert(s);
}
S1.build();S2.build();S1.solve(t);
int l=strlen(t+1);reverse(t+1,t+l+1);
S2.solve(t);
long long ans=0;
for (int i=1;i<l;i++)
ans+=1ll*S1.f[i]*S2.f[l-i];
printf ("%I64d",ans);
return 0;
}
给定长度为 \(n\) 的数组 \(r,a\) 和数字 \(k\) ,\(q\) 次询问给出两个数字 \(x,y\) 表示在强制选择 \(x,y\) 两个位置之后最多能选择多少个位置,使得所有位置满足:记选择中 \(r\) 最大的位置为 \(p\) ,存在一个 \(x\) 满足所有位置的 \(a\) 与 \(a[p]\) 的差小于 \(k\)
\(n\le 10^5,k,a\le 10^9\)
tags : data structures , sortings
考虑计算 \(mx[i]\) 表示当 \(i\) 是最大位置的时候,最多能选择多少位置
容易使用树状数组和扫描线计算
那么再扫描线,按照 \(\max(r_x,r_y)\) 降序排序,把当前所有 \(r>max(r_x,r_y)\) 加入线段树,查询 \(mx\) 数组的区间最值即可
有少量细节
#include <bits/stdc++.h>
using namespace std;
char B[1<<24],*S=B;
#define gc() (*S++)
inline void gi(int&x){
x=0;char e=gc();
for (;e<'0'||e>'9';e=gc());
for (;e>='0'&&e<='9';e=gc()) x=x*10+e-'0';
}
const int N=100005;
#define mid ((l+r)>>1)
int mx[N*12];
inline void insert(int root,int l,int r,int x,int v){
if (l==r){
mx[root]=max(mx[root],v);
return;
}
if (x<=mid) insert(root<<1,l,mid,x,v);
else insert((root<<1)|1,mid+1,r,x,v);
mx[root]=max(mx[root<<1],mx[(root<<1)|1]);
}
inline int query(int root,int l,int r,int L,int R){
if (r<L||l>R) return -1;
if (L<=l&&r<=R) return mx[root];
return max(query(root<<1,l,mid,L,R),query((root<<1)|1,mid+1,r,L,R));
}
int n,k;
int r[N],a[N];
struct Node{
int r,a,id,val;
}t[N],t2[N];
int to[N*3],m;
inline int getpos(int x){
return lower_bound(to+1,to+m+1,x)-to;
}
struct Ask{
int x,y,mx,id;
}q[N];
inline bool cmp(Ask a,Ask b){
return a.mx>b.mx;
}
inline bool cmp2(Node a,Node b){
return a.r<b.r;
}
inline bool cmp3(Node a,Node b){
return a.r>b.r;
}
int Ans[N],Q;
inline void init(){
for (int i=1;i<=n;i++) gi(t[i].r);
for (int i=1;i<=n;i++) gi(t[i].a),to[++m]=t[i].a-k,to[++m]=t[i].a,to[++m]=t[i].a+k;
for (int i=1;i<=n;i++) t[i].id=i;
sort(to+1,to+m+1);
m=unique(to+1,to+m+1)-to-1;
gi(Q);
for (int i=1;i<=Q;i++)
gi(q[i].x),gi(q[i].y),q[i].id=i,
q[i].mx=max(t[q[i].x].r,t[q[i].y].r),
q[i].x=t[q[i].x].a,q[i].y=t[q[i].y].a;
sort(q+1,q+Q+1,cmp);
memset (mx,-1,sizeof(mx));
}
int sum[N*3];
inline int lowbit(int x){return x&(-x);}
inline void update(int x){
for (;x<=m;x+=lowbit(x)) sum[x]++;
}
inline int qsum(int x){
int ans=0;for (;x;x-=lowbit(x)) ans+=sum[x];return ans;
}
inline int query(int x,int y){
return qsum(y)-qsum(x-1);
}
inline void getval(){
sort(t+1,t+n+1,cmp2);
for (int i=1;i<=n;){
int j=i;for (;t[j].r==t[i].r;j++);--j;
for (int p=i;p<=j;p++)
update(getpos(t[p].a));
for (int p=i;p<=j;p++)
t[p].val=query(getpos(t[p].a-k),getpos(t[p].a+k));
i=j+1;
}
}
int main (){
fread(B,1,1<<24,stdin);
gi(n),gi(k);
init();
getval();
memset (mx,-1,sizeof(mx));
int j=1;
sort(t+1,t+n+1,cmp3);
for (int i=1;i<=Q;i++){
while (q[i].mx<=t[j].r&&j<=n) insert(1,1,m,getpos(t[j].a),t[j].val),j++;
if (q[i].x>q[i].y) swap(q[i].x,q[i].y);
Ans[q[i].id]=query(1,1,m,getpos(q[i].y-k),getpos(q[i].x+k));
}
for (int i=1;i<=Q;i++) printf ("%d\n",Ans[i]);
return 0;
}给定一棵树,支持三种操作:
\(n\le 10^5,q\le 10^5\)
tags : data structures , trees
首先考虑如何求出 \(root=r\) 时候的 \(lca(u,v)\)
可以这样看,实际上 \(lca(u,v)\) 就是 \(u.v\) 各做一次到 \(root\) 链 \(+1\) 之后权值为 \(2\) 的点的深度最大的一个
那么转化为求链并即可求出 \(lca(u,v)\)
考虑如何修改,讨论一波即可
#include <bits/stdc++.h>
using namespace std;
const int N=100005;
#define ll long long
int a[N];
int n,q;
struct Tree {
int Head[N],Next[N<<1],Adj[N<<1],tot;
inline void addedge(int u,int v) {
Next[++tot]=Head[u],Head[u]=tot,Adj[tot]=v;
Next[++tot]=Head[v],Head[v]=tot,Adj[tot]=u;
}
int fa[N],deep[N],son[N],top[N],size[N];
inline void dfs(int x,int f) {
size[x]=1;
for (int e=Head[x]; e; e=Next[e])
if (Adj[e]!=f) {
fa[Adj[e]]=x;
deep[Adj[e]]=deep[x]+1;
dfs(Adj[e],x);
size[x]+=size[Adj[e]];
son[x]=(size[son[x]]<size[Adj[e]]?Adj[e]:son[x]);
}
}
int dfn[N],to[N],Time;
inline void dfs2(int x,int tp) {
top[x]=tp,dfn[x]=++Time,to[Time]=x;
if (!son[x]) return;
dfs2(son[x],tp);
for (int e=Head[x]; e; e=Next[e])
if (Adj[e]!=fa[x]&&Adj[e]!=son[x])
dfs2(Adj[e],Adj[e]);
}
inline int LCA(int u,int v) {
for (; top[u]!=top[v]; deep[top[u]]<deep[top[v]]?v=fa[top[v]]:u=fa[top[u]]);
return deep[u]<deep[v]?u:v;
}
ll tag[N<<2],sum[N<<2];
#define mid ((l+r)>>1)
inline void pushdown(int root,int l,int r) {
if (tag[root]) {
tag[root<<1]+=tag[root];
tag[(root<<1)|1]+=tag[root];
sum[root<<1]+=1ll*tag[root]*(mid-l+1);
sum[(root<<1)|1]+=1ll*tag[root]*(r-mid);
tag[root]=0;
}
}
inline void build(int root,int l,int r) {
if (l==r) {
sum[root]=a[to[l]];
return;
}
build(root<<1,l,mid);
build((root<<1)|1,mid+1,r);
sum[root]=sum[root<<1]+sum[(root<<1)|1];
}
inline void update(int root,int l,int r,int L,int R,int v) {
if (r<L||l>R) return;
if (L<=l&&r<=R) {
tag[root]+=v;
sum[root]+=1ll*(r-l+1)*v;
return;
}
pushdown(root,l,r);
update(root<<1,l,mid,L,R,v);
update((root<<1)|1,mid+1,r,L,R,v);
sum[root]=sum[root<<1]+sum[(root<<1)|1];
}
inline ll query(int root,int l,int r,int L,int R) {
if (r<L||l>R) return 0;
if (L<=l&&r<=R) return sum[root];
pushdown(root,l,r);
return query(root<<1,l,mid,L,R)+query((root<<1)|1,mid+1,r,L,R);
}
inline int qlca(int root,int x,int y) {
int lca1=LCA(x,y),lca2=LCA(root,x),lca3=LCA(root,y),t=0;
if (deep[lca1]>deep[t]) t=lca1;
if (deep[lca2]>deep[t]) t=lca2;
if (deep[lca3]>deep[t]) t=lca3;
return t;
}
inline int jump(int root,int u) {
int v=root;
while(top[v]!=top[u]) {
if(fa[top[v]]==u)return top[v];
v=fa[top[v]];
}
return son[u];
}
inline void modify(int root,int x,int y,int v) {
int t=qlca(root,x,y);
if (t==root) {
update(1,1,n,1,n,v);
return;
}
if (dfn[root]<dfn[t]||dfn[root]>dfn[t]+size[t]-1) {
update(1,1,n,dfn[t],dfn[t]+size[t]-1,v);
return;
}
t=jump(root,t);
update(1,1,n,1,n,v);
update(1,1,n,dfn[t],dfn[t]+size[t]-1,-v);
}
inline ll ask(int root,int x) {
if (root==x) return sum[1];
else if (dfn[root]<dfn[x]||dfn[root]>dfn[x]+size[x]-1) return query(1,1,n,dfn[x],dfn[x]+size[x]-1);
x=jump(root,x);
return query(1,1,n,1,n)-query(1,1,n,dfn[x],dfn[x]+size[x]-1);
}
} T;
int main () {
scanf ("%d%d",&n,&q);
for (int i=1; i<=n; i++) scanf ("%d",&a[i]);
for (int i=1; i<n; i++) {
int u,v;
scanf ("%d%d",&u,&v);
T.addedge(u,v);
}
T.dfs(1,0),T.dfs2(1,1);
T.build(1,1,n);
T.deep[0]=-1;
int rt=1;
while (q--) {
int opt;
scanf ("%d",&opt);
if (opt==1) {
scanf ("%d",&rt);
} else if (opt==2) {
int x,y,z;
scanf ("%d%d%d",&x,&y,&z);
T.modify(rt,x,y,z);
} else {
int x;
scanf ("%d",&x);
printf ("%lld\n",T.ask(rt,x));
}
}
return 0;
}
在一条路上修 \(n\) 栋高度为 \([0,h]\) 的房子,假设修了一栋高度为 \(a\) 的房子就会产生收益 \(a^2\)。有 \(m\) 个限制,每个限制\(l,r,x,c\),表示在 \([l,r]\) 这些房子中,如果最高的房子严格大于了 \(x\) ,就要交 \(c\) 的罚款。
求最大收益。
\(n,m,h\le 50\)
tags : dp , flows , graphs
最小割,切糕模型,考虑用总答案减去无法得到的贡献/需要承担的损失,建图方法如下图
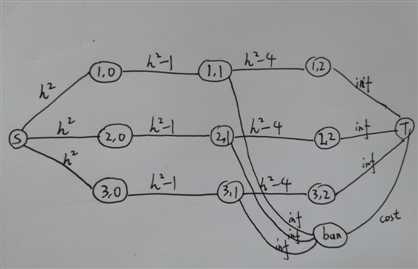
#include <bits/stdc++.h>
using namespace std;
const int N=10005,E=1000005;
int Head[N],Next[E],Adj[E],Flow[E],tot=1;
inline void addedge(int u,int v,int w){
Next[++tot]=Head[u],Head[u]=tot,Adj[tot]=v,Flow[tot]=w;
Next[++tot]=Head[v],Head[v]=tot,Adj[tot]=u,Flow[tot]=0;
}
int S,T,level[N];
int Q[N];
int to[55][55];
inline bool bfs(){
memset (level,-1,sizeof(level));
int l=1,r=0;
Q[++r]=S,level[S]=0;
while (l<=r){
int x=Q[l++];
for (int e=Head[x];e;e=Next[e])
if (level[Adj[e]]==-1&&Flow[e])
level[Adj[e]]=level[x]+1,Q[++r]=Adj[e];
}
return level[T]!=-1;
}
inline int dfs(int x,int flow){
if (x==T||!flow) return flow;
int ret=0,c;
for (int e=Head[x];e;e=Next[e])
if (level[Adj[e]]==level[x]+1&&Flow[e]&&(c=dfs(Adj[e],min(flow-ret,Flow[e])))){
ret+=c;Flow[e]-=c,Flow[e^1]+=c;
if (ret==flow) break;
}
if (!ret) level[x]=-1;
return ret;
}
int cnt=0;
int main (){
int n,m,h;scanf ("%d%d%d",&n,&h,&m);
int ans=h*h*n;S=n*(h+1)+m+1,T=n*(h+1)+m+2;
for (int i=1;i<=n;i++)
for (int j=0;j<=h;j++)
to[i][j]=++cnt;
for (int i=1;i<=n;i++)
addedge(S,to[i][0],1<<30);
for (int i=1;i<=n;i++)
for (int j=0;j<h;j++)
addedge(to[i][j],to[i][j+1],h*h-j*j);
for (int i=1;i<=m;i++){
int l,r,x,c;scanf ("%d%d%d%d",&l,&r,&x,&c);
if (x==h) continue;++cnt;++x;
for (int j=l;j<=r;j++)
addedge(to[j][x],cnt,1<<30);
addedge(cnt,T,c);
}
while (bfs()) ans-=dfs(S,1<<30);
printf ("%d",ans);
return 0;
}有一个容量为 \(k\) 的空书架,现在共有 \(n\) 个请求,每个请求给定一本书 \(a_i\) ,如果你的书架里没有这本书,你就必须以 \(c_i\) 的价格购买这本书放入书架。当然,你可以在任何时候丢掉书架里的某本书。请求出完成这 \(n\) 个请求所需要的最少价钱。
\(1\le n,k\le 80,1\le a_i\le n,0\le c_i\le 10^6\)
tags:flows
费用流,挺常规的建模方法
考虑每天强制买进书,如果不留,那就视为买了就扔,如果留到下一次,那么视为买了就卖,卖了赚的前恰好为 \(c_{a_i}\)
于是拆点,把买和不买拆成两个点 \(A,B\)
表示每本书价格,连边 \(S\to A_i\) ,容量为 \(1\) ,费用为 \(c_{a_i}\)
表示每本书留到最后的,连边 \(B_i\to T\) ,容量为 \(1\) ,费用为 \(0\)
因为强制买书,所以每天只留下 \(k-1\) 本书,连边 \(A_i\to A_{i+1}\) ,容量为 \(k\) ,费用为 \(0\)
如果表示买了就扔,连边 $A_i\to B_i $ ,容量为 \(1\) ,费用为 \(0\)
记 \(pos[i]\) 表示书 \(i\) 上一次出现的位置,那么\(A_{i-1}\to B_{pos[i]}\) ,容量为 \(1\) ,费用为 \(-c_{a_i}\)
跑最小费用流即可
#include <bits/stdc++.h>
using namespace std;
const int N=85*4,E=N*N;
int Head[N],Next[E],Adj[E],Flow[E],Weight[E],tot=1;
queue <int > Q;
int n,k,s,t;
int a[N],c[N],pos[N];
inline void addedge(int u,int v,int f,int w){
Next[++tot]=Head[u],Head[u]=tot,Adj[tot]=v,Flow[tot]=f,Weight[tot]=w;
Next[++tot]=Head[v],Head[v]=tot,Adj[tot]=u,Flow[tot]=0,Weight[tot]=-w;
}
inline int Min(int a,int b){
return a<b?a:b;
}
int point[N],edge[N],dis[N];
bool vis[N];
inline bool Spfa(){
memset (dis,0x3f,sizeof(dis));
memset (point,-1,sizeof(point));
dis[s]=0;Q.push(s);
while (!Q.empty()){
int x=Q.front();Q.pop();vis[x]=false;
for (int e=Head[x];e;e=Next[e])
if (dis[x]+Weight[e]<dis[Adj[e]]&&Flow[e]){
dis[Adj[e]]=dis[x]+Weight[e];
point[Adj[e]]=x,edge[Adj[e]]=e;
if (!vis[Adj[e]]) vis[Adj[e]]=true,Q.push(Adj[e]);
}
}
return point[t]!=-1;
}
int ans1=0,ans2=0;
inline void work(){
int f=1<<30;
for (int x=t;x!=s;x=point[x]) f=Min(f,Flow[edge[x]]);ans1+=f;
for (int x=t;x!=s;x=point[x]) Flow[edge[x]]-=f,Flow[edge[x]^1]+=f,ans2+=f*Weight[edge[x]];
}
int main () {
scanf ("%d%d",&n,&k);
s=n*2+1,t=n*2+2;
for (int i=1;i<=n;i++) scanf ("%d",&a[i]);
for (int i=1;i<=n;i++) scanf ("%d",&c[i]);
for (int i=1;i<=n;i++){
addedge(s,i,1,c[a[i]]);
addedge(i+n,t,1,0);
addedge(i,i+n,1,0);
if (pos[a[i]]) addedge(i-1,pos[a[i]]+n,1,-c[a[i]]);
pos[a[i]]=i;
}
for (int i=1;i<n;i++) addedge(i,i+1,k-1,0);
while (Spfa()) work();
printf ("%d",ans2);
return 0;
}
一个长度为\(n\)的序列,上面每个位置有一种颜色,求把这个序列分割成若干段,使得每一段的只出现一次的颜色个数不超过\(k\)个,求方案数。
\(n \le 10^5\)
tags : data structures , dp
设\(dp[i]\)表示\(1...i\)的合法划分方案数
显然 \(dp[i]=\sum_{j=1}^{i-1}dp[j][cnt(j,i) \le k]\)
对于\(cnt(j,i)\)的计算:
定义数组\(b\),如果\([i,j]\)中\(a_j\)的颜色第一次出现,那么\(b_j=1\),如果是第二次出现,那么\(b_j=-1\),否则\(b_j=0\)
那么\(cnt(j,i)=\sum_{k=j}^ib_k\)
考虑\(i\)转移到\(i+1\)的过程,我们发现只有一个\(b_p\)从\(1\)变成\(-1\) ,有一个\(b_q\)从\(-1\)变成\(0\)
考虑\(cnt(j,i+1)\)相对于\(cnt(j,i)\)的变化本质就是\([p+1,i]\)区间\(+1\),区间\([q+1,p]-1\),其余不变
那么我们需要支持两种操作:
使用分块维护
时间复杂度\(O(n\sqrt n)\)
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
char B[1<<21],*S=B;
#define gc() (*S++)
inline int gi(){
int x=0;char e=gc();
for (;e<'0'||e>'9';e=gc());
for (;e>='0'&&e<='9';e=gc()) x=(x<<1)+(x<<3)+(e^48);
return x;
}
const int N=200001,sqrtN=317;
const int Mod=998244353;
int block,size,n,k;
int bel[N],tag[sqrtN],L[N],R[N];
int cnt[sqrtN][N],dp[N];
int b[N],pre[N],last[N];
inline int Max(int a,int b){return a>b?a:b;}
inline int Min(int a,int b){return a<b?a:b;}
inline void c1(int&a,int b){a+=b;a=(a>=Mod?a-Mod:a);}
inline void c2(int&a,int b){a-=b;a=(a<0?a+Mod:a);}
inline void init(){
size=sqrt(n);block=n/size+(n%size!=0);dp[0]=1;
for (int i=1;i<=n;i++) bel[i]=(i-1)/size+1;
for (int i=1;i<=n;i++) if (bel[i]==bel[i-1]) L[i]=L[i-1];else L[i]=i;
for (int i=n;i>=1;i--) if (bel[i]==bel[i+1]) R[i]=R[i+1];else R[i]=i;
}
int ans;
inline void del(int x){
c1(ans,cnt[x][k-tag[x]+1+n]);
tag[x]--;
}
inline void add(int x){
c2(ans,cnt[x][k-tag[x]+n]);
tag[x]++;
}
inline void work(int x,int y){
if (b[x]+tag[bel[x]]<=k) c2(ans,dp[x-1]);
c2(cnt[bel[x]][b[x]+n],dp[x-1]);
b[x]+=y;
if (b[x]+tag[bel[x]]<=k) c1(ans,dp[x-1]);
c1(cnt[bel[x]][b[x]+n],dp[x-1]);
}
inline void update(int l,int r,int val){
if (l>r) return;
int x=bel[l],y=bel[r];
if (x==y) for (int i=l;i<=r;i++) work(i,val);
else{
for (int i=l;i<=R[l];i++) work(i,val);
for (int i=L[r];i<=r;i++) work(i,val);
for (int i=x+1;i<y;i++)
if (val==1) add(i);
else del(i);
}
}
inline void insert(int x,int y){
b[x]-=tag[bel[x]];
c1(ans,y);
c1(cnt[bel[x]][b[x]+n],y);
}
int main (){
fread(B,1,1<<21,stdin);
n=gi(),k=gi();
for (int i=1,a;i<=n;i++) a=gi(),pre[i]=last[a],last[a]=i;
init();insert(1,1);
for (int i=1;i<=n;i++) {
update(pre[i]+1,i,1);
update(pre[pre[i]]+1,pre[i],-1);
dp[i]=ans;
insert(i+1,dp[i]);
}
printf ("%d",dp[n]);
return 0;
}求有多少个数字 \(k\) 满足存在一个字符串
\(a,b\le 10^9\)
tags : binary search , implementation , math
对于一个合法的 \(k\) 而言,设 \(p\) 表示循环节的数量,满足 \(k=\lfloor\frac{n}{p}\rfloor\) ,设 \(c_a\) 表示一个整段循环节里 \(A\) 的个数,\(c_b\) 表示一个整段循环节里 \(B\) 的个数,显然有 \(c_a+c_b=k\) , $ c_a\le \lfloor\frac{a}{p}\rfloor$ , $ c_b\le \lfloor\frac{b}{p}\rfloor$
边角部分显然小于整段,那么一定有 $ c_a\ge \lceil\frac{a}{p+1}\rceil$ , $ c_b\ge \lceil\frac{b}{p+1}\rceil$
综合一下,需要满足的是
\[
\lceil\frac{a}{p+1}\rceil\le c_a\le \lfloor\frac{a}{p}\rfloor\\lceil\frac{b}{p+1}\rceil\le c_b\le \lfloor\frac{b}{p}\rfloor
\]
对 \(p\) 数论分块,复杂度 \(O(\sqrt{a+b})\)
#include <bits/stdc++.h>
using namespace std;
int main (){
int a,b;scanf ("%d%d",&a,&b);
int n=a+b,ans=0;
for (int l=1,r;l<=n;l=r+1){
int p=n/l;r=n/p;
if (a<p||b<p) continue;
int l1=(a+p)/(p+1),r1=a/p;
int l2=(b+p)/(p+1),r2=b/p;
if (l1<=r1&&l2<=r2)
ans+=max(0,min(r,r1+r2)-max(l,l1+l2)+1);
}
printf ("%d",ans);
return 0;
}
平面上有一堆点,你要求五角星的数量,保证不存在三点共线。
\(n\le 300\)
tags : dp , geometry
五角星个数等价于 \(5\) 个点都在它们的凸包上的五元组个数,就是找 \(5\) 条极角序上升的线段。
设 \(f[i][j][5]\) 表示从 \(i\) 出发,当前节点为 \(j\) ,已经确定了 \(1\dots5\) 条边的方案数
#include <bits/stdc++.h>
using namespace std;
const int N=305;
#define ll long long
struct Node{
int x,y;
}p[N];
ll dp[N][N][5];
inline ll cross(Node a,Node b){
return 1ll*a.x*b.y-1ll*a.y*b.x;
}
Node operator - (Node a,Node b){return (Node){a.x-b.x,a.y-b.y};}
Node operator + (Node a,Node b){return (Node){a.x+b.x,a.y+b.y};}
bool operator < (Node a,Node b){return cross(a,b)<0;}
struct Line{
Node v;
int a,b;
};vector <Line > E;
bool operator < (Line a,Line b){
if (a.v<b.v) return true;
if (b.v<a.v) return false;
if (a.a!=b.a) return a.a<b.a;
return a.b<b.b;
}
int main (){
int n;scanf ("%d",&n);
for (int i=1;i<=n;i++)
scanf ("%d%d",&p[i].x,&p[i].y);
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
if (i!=j) E.push_back((Line){p[j]-p[i],i,j});
sort(E.begin(),E.end());
for (int t=0;t<E.size();t++){
int u=E[t].a,v=E[t].b;
dp[u][v][0]++;
for (int i=0;i<5;i++)
for (int j=1;j<=n;j++)
dp[j][v][i+1]+=dp[j][u][i];
}
ll ans=0;
for (int i=1;i<=n;i++) ans+=dp[i][i][4];
printf ("%lld",ans);
return 0;
}
记\(lcp(i,j)\)表示i这个后缀和\(j\)这个后缀的最长公共前缀长度
给定一个字符串,每次询问的时候给出两个正整数集合\(A\)和\(B\),求\(∑_{i∈A,j∈B}lcp(i,j)\) 的值
\(n,q \le 10^5\), \(\sum_{i=1}^q |A_i|,\sum_{i=1}^q|B_i|\le 2\times 10^5\)
考虑对于原串构造后缀树,对于每一次询问建出虚树,\(lcp(i,j)\)即为\(i\),\(j\)在后缀树上对应节点的\(LCA\)深度
时间复杂度\(O((\sum_{i=1}^q |A_i|+\sum_{i=1}^q|B_i|)*logn)\)
有些难码
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline", "no-stack-protector", "unroll-loops")
#pragma GCC diagnostic error "-fwhole-program"
#pragma GCC diagnostic error "-fcse-skip-blocks"
#pragma GCC diagnostic error "-funsafe-loop-optimizations"
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
namespace io {
const int SIZE = (1 << 21) + 1;
char ibuf[SIZE], *iS, *iT, obuf[SIZE], *oS = obuf, *oT = oS + SIZE - 1, c, qu[55];
int f, qr;
#define gc() (iS == iT ? (iT = (iS = ibuf) + fread (ibuf, 1, SIZE, stdin), (iS == iT ? EOF : *iS ++)) : *iS ++)
inline void flush () {
fwrite (obuf, 1, oS - obuf, stdout);
oS = obuf;
}
inline void putc (char x) {
*oS ++ = x;
if (oS == oT) flush ();
}
template <class I>
inline void gi (I &x) {
for (c = gc(); c < '0' || c > '9'; c = gc());
for (x = 0; c <= '9' && c >= '0'; c = gc()) x =(x << 1) +(x << 3) +(c & 15);
}
template <class I>
inline void print (I x) {
if (!x) putc ('0');
if (x < 0) putc ('-'), x = -x;
while (x) qu[++ qr] = x % 10 + '0', x /= 10;
while (qr) putc (qu[qr --]);
}
inline void getc(char&x){
x=gc();for (;x<'a'||x>'z';x=gc());
}
struct Flusher_ {
~Flusher_() {
flush();
}
} io_flusher_;
}
using io :: gi;
using io :: putc;
using io :: getc;
using io :: print;
const int N=400005;
struct SAM{
int ch[N][26],fa[N],len[N],id[N],cnt,last;
inline void init(){cnt=last=1;}
inline void insert(int i,int c){
int np=++cnt,p=last;last=cnt,len[np]=len[p]+1,id[i]=np;
for (;p&&!ch[p][c];p=fa[p]) ch[p][c]=np;
if (!p) fa[np]=1;
else{
int q=ch[p][c];
if (len[p]+1==len[q]) fa[np]=q;
else{
int nq=++cnt;len[nq]=len[p]+1;
memcpy(ch[nq],ch[q],sizeof(ch[q]));
fa[nq]=fa[q],fa[q]=fa[np]=nq;
for (;ch[p][c]==q;p=fa[p]) ch[p][c]=nq;
}
}
}
int Head[N],Next[N],Adj[N],tot=0;
inline void addedge(int u,int v){
Next[++tot]=Head[u];
Head[u]=tot;
Adj[tot]=v;
}
inline void build(){
for (int i=2;i<=cnt;i++) addedge(fa[i],i);
}
int sz[N],dep[N],top[N],son[N];
int dfn[N],Time=0;
inline void dfs(int x){
sz[x]=1,dfn[x]=++Time;
for (int e=Head[x];e;e=Next[e]){
dep[Adj[e]]=dep[x]+1;
dfs(Adj[e]);
sz[x]+=sz[Adj[e]];
son[x]=(sz[son[x]]>sz[Adj[e]]?son[x]:Adj[e]);
}
}
inline void dfs2(int x,int tp){
top[x]=tp;
if (!son[x]) return;
dfs2(son[x],tp);
for (int e=Head[x];e;e=Next[e])
if (Adj[e]!=son[x]) dfs2(Adj[e],Adj[e]);
}
inline int LCA(int u,int v){
for (;top[u]!=top[v];dep[top[u]]>dep[top[v]]?u=fa[top[u]]:v=fa[top[v]]);
return dep[u]<dep[v]?u:v;
}
}sam;
#define ll long long
ll ans=0;
int a[N];
inline bool cmp(int a,int b){
return sam.dfn[a]<sam.dfn[b];
}
struct Tree{
int n;
int Head[N<<1],Next[N<<2],Adj[N<<2],tot=0;
int s[N<<1],used[N<<1],C=0,top=0;
inline void init(){
for (int i=1;i<=tot;i++) Next[i]=Adj[i]=0;
for (int i=1;i<=C;i++) Head[used[i]]=cnt1[used[i]]=cnt2[used[i]]=0;
C=0,tot=0;
}
inline void addedge(int u,int v){
Next[++tot]=Head[u];
Head[u]=tot;
Adj[tot]=v;
}
int cnt1[N],cnt2[N];
inline void dfs(int x){
// fprintf (stderr,"%d\n",x);
ans+=1ll*sam.len[x]*(cnt1[x]*cnt2[x]);
for (int e=Head[x];e;e=Next[e]){
dfs(Adj[e]);
ans+=1ll*sam.len[x]*cnt1[x]*cnt2[Adj[e]];
ans+=1ll*sam.len[x]*cnt2[x]*cnt1[Adj[e]];
cnt1[x]+=cnt1[Adj[e]],cnt2[x]+=cnt2[Adj[e]];
cnt1[Adj[e]]=cnt2[Adj[e]]=0;
}
}
void insert(int x) {
if (top<=1) {s[++top]=x;return;}
int lca=sam.LCA(x,s[top]);
if (lca==s[top]) {s[++top]=x;return;}
while (top>1&&sam.dfn[s[top-1]]>=sam.dfn[lca]) addedge(s[top-1],s[top]),top--;
if (lca!=s[top]) addedge(lca,s[top]),s[top]=lca;s[++top]=x,used[++C]=lca;
}
void build(int x){
for (int i=1;i<=x;i++) cnt1[a[i]]++;
for (int i=x+1;i<=n;i++) cnt2[a[i]]++;
sort(a+1,a+n+1,cmp);
s[top=1]=1,used[C=1]=1;
for (int i=1;i<=n;i++) if (a[i]!=1&&a[i]!=a[i-1]) used[++C]=a[i],insert(a[i]);
while (top>0) addedge(s[top-1],s[top]),top--;
}
}T;
char s[N];
int main (){
// freopen ("a.in","r",stdin);
// freopen ("a.out","w",stdout);
int n,m;
gi(n),gi(m);
for (int i=1;i<=n;i++) getc(s[i]);
sam.init();
for (int i=n;i>=1;i--) sam.insert(i,s[i]-'a');
sam.build();
sam.dfs(1);
sam.dfs2(1,1);
// fprintf (stderr,"%d\n",sam.LCA(8,7));puts("");
while (m--){
T.init();
int x,y;gi(x),gi(y);T.n=x+y;
for (int i=1;i<=x;i++) gi(a[i]),a[i]=sam.id[a[i]];
for (int i=1;i<=y;i++) gi(a[i+x]),a[i+x]=sam.id[a[i+x]];
T.build(x);
ans=0;
T.dfs(1);
print(ans),putc('\n');
}
return 0;
}标签:top uniq 问题 ror scanf 个数 oss 高度 字符串
原文地址:https://www.cnblogs.com/crazyzh/p/11619831.html