标签:while sizeof info ons set pos 增加 就是 return
填坑
死磕成功
仔细回想,二分答案还是很明显的
接下来是如何判断的问题
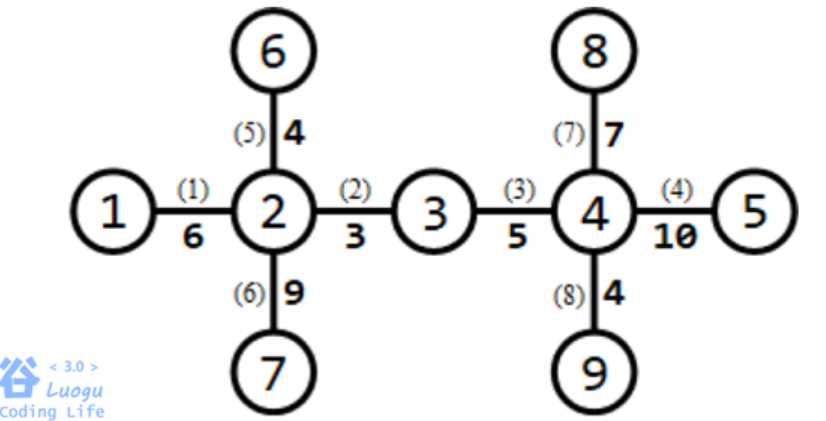
就以样例为例子好了
我的目的是贪心选出越多长度大于mid的路径
首先,对于一条道路,如果它的长度大于等于mid,那么我们直接让sum++,直接删除这条边即可
事实上,对于以u为根的子树,经过u的路径有两种情况:
1.儿子->儿子
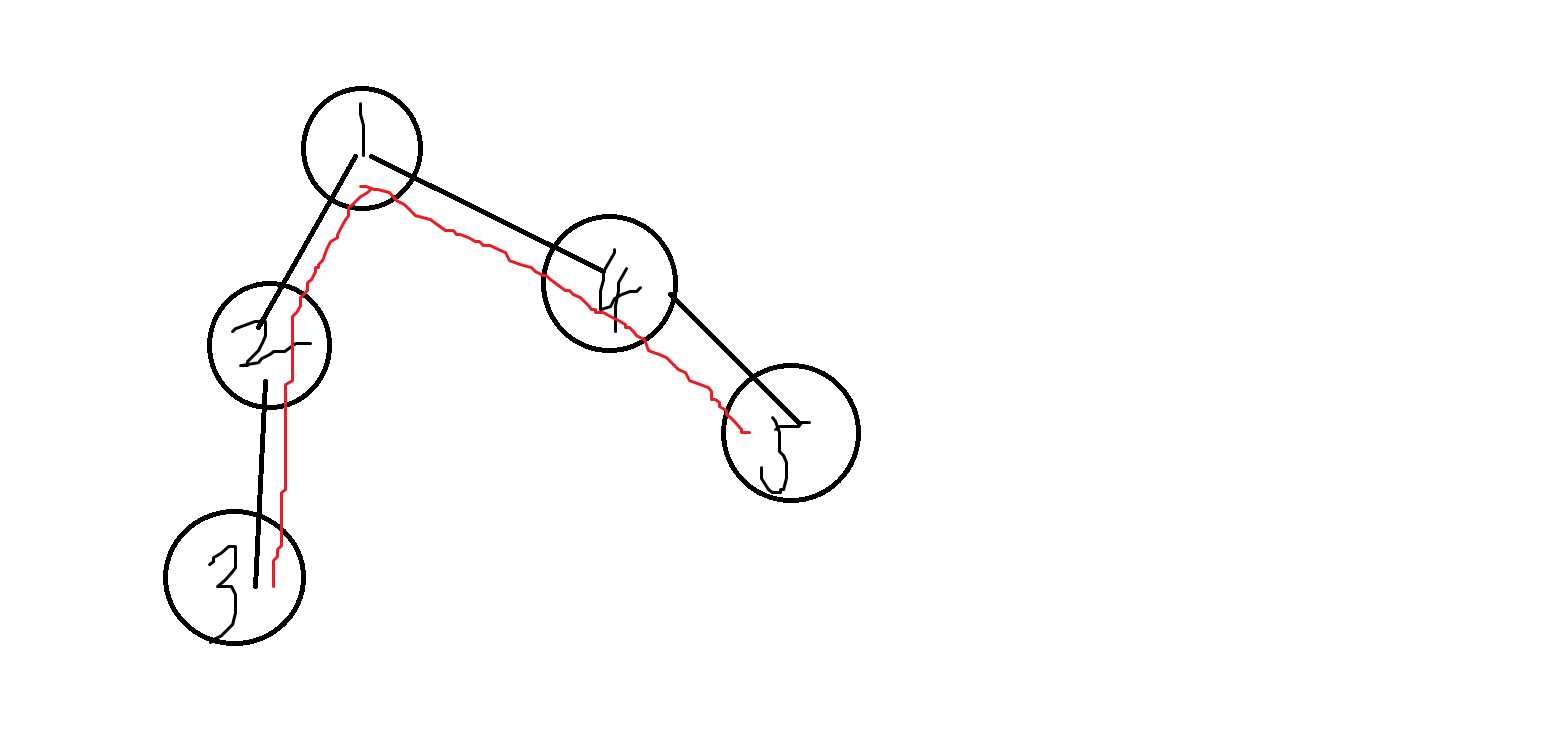
如图,这条选中的红色路径把1当作中介,增加了一个答案
2.儿子->父亲
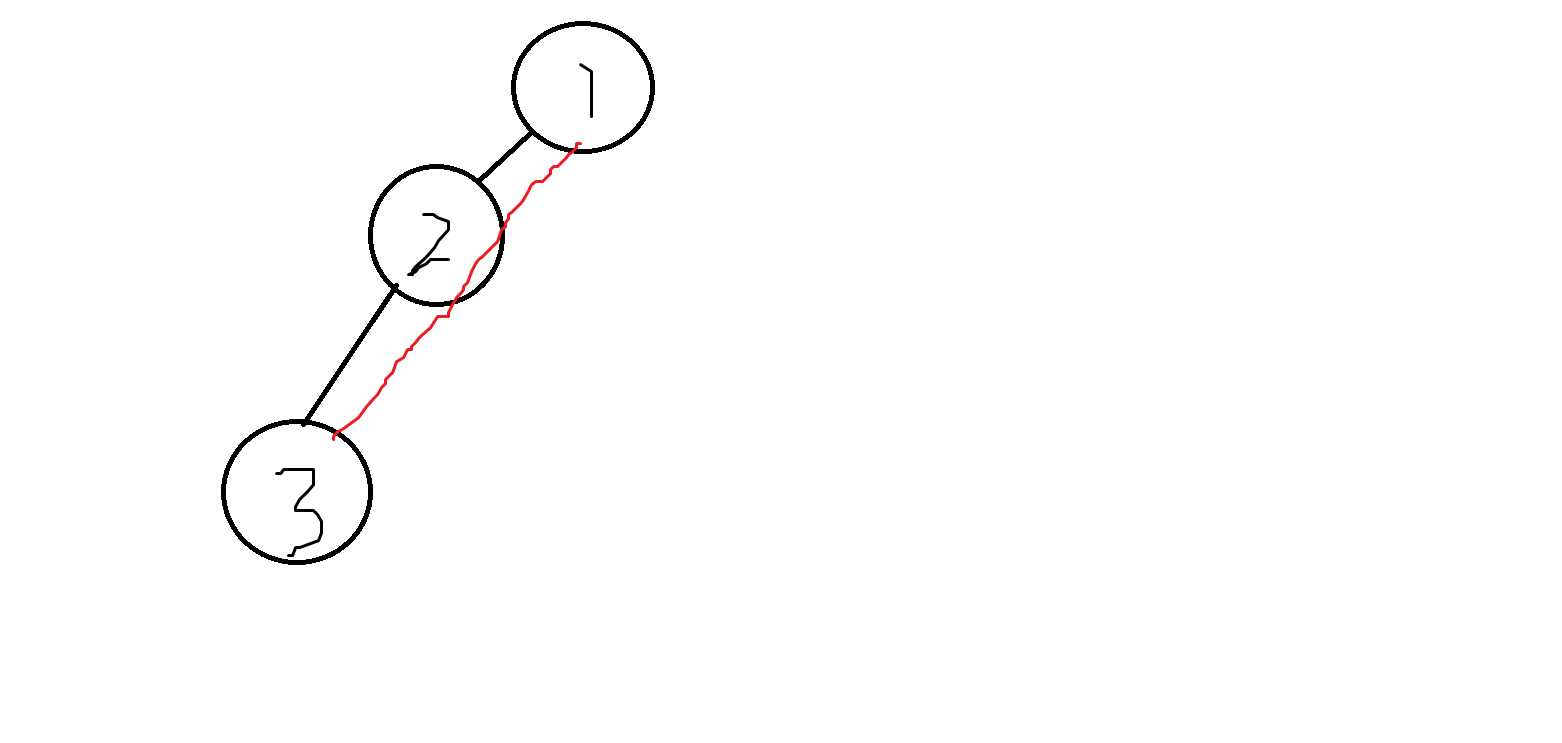
如图,红色路径即为所求
然后我们就开始了贪心策略
首先,对于节点u,我们先获取所有u的儿子v能上传的路径
如果一个v的路径已经>=mid,直接sum++
接着,把其他<mid的儿子上传的路径丢入multiset中
每次取出一个最小值p,分两种情况:
1.能找到一条>=(mid-p)的路径:两条路径删除,sum++
2.找不到:能上传给u父亲的最长路径l变为max(l,p)
对于每个节点,都开一个multiset
这样,我在luogu就被卡常了
还有一个优化,就是把二分上界r设为树的直径
可以优化1.5s
代码:
#include<bits/stdc++.h> using namespace std; #define il inline typedef long long ll; #define re register const int N=50005; int n,m; int hed[N],tal[N<<1],nxt[N<<1],cnt=0; ll val[N<<1]; ll l=1,r=0,mid; ll ans=-1; ll dis[N]; int sum; il ll llmax(ll x,ll y){ return x>y?x:y; } il void addege(int x,int y,ll z){ cnt++; tal[cnt]=y; val[cnt]=z; nxt[cnt]=hed[x]; hed[x]=cnt; } il ll dfs(int u,int fa){ multiset<ll> s; for(re int i=hed[u];i;i=nxt[i]){ int v=tal[i]; if(v==fa) continue; ll value=val[i]+dfs(v,u); if(value>=mid){ sum++; } else{ s.insert(value); } } ll l=0; while(!s.empty()){ ll p=*s.begin(); s.erase(s.begin()); multiset<ll>::iterator it=s.lower_bound(mid-p); if(it!=s.end()){ s.erase(it); sum++; } else{ l=llmax(l,p); } } return l; } il bool check(){ sum=0; dfs(1,1); return sum>=m; } il void Dfs(int u,int fa){ for(re int i=hed[u];i;i=nxt[i]){ int v=tal[i]; if(v==fa) continue; dis[v]=dis[u]+val[i]; Dfs(v,u); } } il void cal(){ memset(dis,0,sizeof(dis)); int pos=1; Dfs(pos,pos); for(re int i=2;i<=n;i++){ if(dis[i]>dis[pos]) pos=i; } memset(dis,0,sizeof(dis)); Dfs(pos,pos); for(re int i=1;i<=n;i++){ if(dis[i]>dis[pos]) pos=i; } r=dis[pos]; //cout<<r<<endl; } int main(){ scanf("%d%d",&n,&m); for(re int i=1;i<n;i++){ int x,y; ll z; scanf("%d%d%lld",&x,&y,&z); addege(x,y,z); addege(y,x,z); } cal(); while(l<=r){ mid=(l+r)/2ll; if(check()) ans=mid,l=mid+1; else r=mid-1; } printf("%lld\n",ans); return 0; }
标签:while sizeof info ons set pos 增加 就是 return
原文地址:https://www.cnblogs.com/QYJ060604/p/11620056.html