标签:表达式 观察 四种 设置 最大独立集 倍增 san lang min
HDU5093

同一行或者同一列,并且没有障碍
n,m<=100
感觉是二分图?
咋感觉出来的???
没有障碍的情况:一行最多放一个,一列最多放一个
或者说一个物体用掉一行一列
二分图:左边代表每一行,右边代表每一列

由于没有障碍物,左边的每一个点都会向右边每一个点连一条边
匹配的结果就是min(n,m)
怎么解决障碍物?
障碍物的作用:占了一个格子,把每行拆成两部分,每列拆成两部分
比如一行有两个障碍,这一行就是三个部分,那么把这三个部分建三个点,列同理
那么得到一张新的二分图
然后跑一遍匈牙利就好了
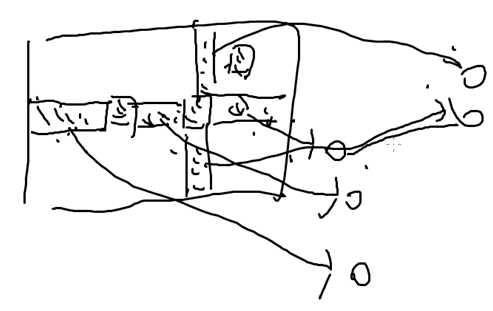

对角线指左上到右下
二分图
左边的点是行,右边是列
保证一开始选出来的1不在同一行,同一列
如果(i,j)是1,就把左边的i和右边的j连边,看看最后的最大匹配数是不是大于等于N

有n个bool变量x1~xn,有m个位运算的表达式(只有两个变量),求是否有一种方法使得m个表达式都成立
对于每一个变量建两个点,一个是true,一个是false。边就从m个表达式来
比如x1&x2=false --> x1==false||x2==false
从x1的true向x2的false连一条有向边,代表x1=true时,x2=false
从x2的true向x1的false连一条有向边,代表x2=true时,x1=false
这个边实际上代表一种推导关系
x2||x3=true --> 从x2的false向x3的true连边,从x3的false向x2的true连边
x4&x5=true --> x4=true x5=true
如果x4必须等于true,就把x4=false向x4的false连边,x5同理
怎么判断有无解?
如果某一个点的true出发能够走到他的false,从false也能走到true,就说明误解
也就是说一个变量的两个取值在同一个强连通分量内
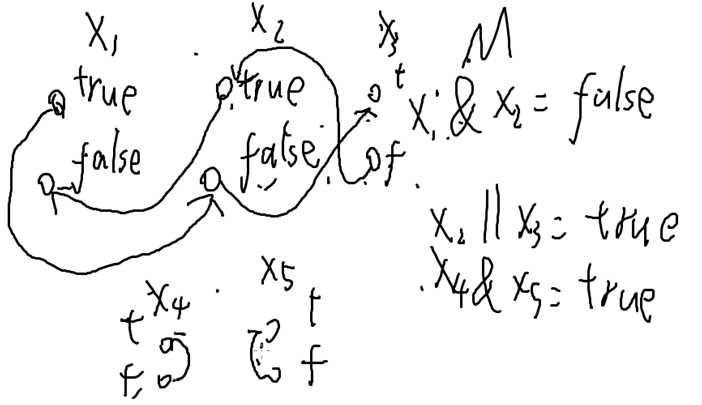
先建图,然后跑tarjan,如果有一个变量的两个取值在同一个强连通分量内就无解

所有炸弹爆炸的最小值最大是多少
既然最小的是r,不如让所有的都是r
怎么判断有解?
要么选第一个炸弹,要么选第二个炸弹,对应2-sat的两种取值
如果两个炸弹能够互相炸到,就说明他俩不能同时选,那么就把一个向另一个建边
N^3暴力建边然后tarjan
二分+2-sat
欧拉回路和哈密尔顿回路?先咕着。。
安利一个查题的网站 vjudge.net(但是貌似不太稳定)

骨牌的黑色必须对应黑色,白色必须对应白色,并且骨牌不重叠
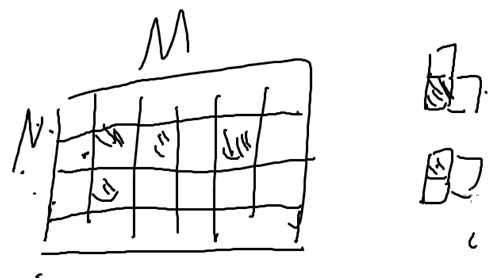
n,m<=50?
n,m<=100?
n,m<=1000?
1.
有一些格子有障碍,不能放置骨牌
如果骨牌是1*2的话,黑格子和白格子二分图匹配
一个黑格子配两个白格子?
把一个黑的变成两个黑的?这样就能两个配两个。但是把一个黑点拆成两个黑点,向周围的四个白点连线,有可能会出现两个黑点分别选择左右或者上下的情况。怎么改?
L形有四种情况,即选的白格子为上左,上右,下左,下右。
那么只需要把黑格子拆成两个黑格子,一个连上下,一个连左右
看看所有的黑格子,白格子有没有被匹配上,如果匹配完了的话就说明可以
2.
n,m<=1000
S-SAT
四种不同的取值 sat4之后、我问题
左右选点,上下选点,为每一个节点设置两个变量
曼哈顿距离不超过2的两个黑格子建边,2-sat,复杂度o(nm)


变量:每个提案被通过还是否决0/1
建边:每个人会对不超过4个提案进行投票?
如果只投了一票反对票,那么这个提案必须被否决。把这个提案的同意向否决连边
如果两票,则都要满足
如果三票,至多有一票不被满足,枚举是哪一票
如果四票,仍然是至多一票不被满足,同上一种情况
建完图之后,如果一个提案的通过能走到它自己的否决,就必须选择否决,如果否决能走到通过,就必须选择通过。
否则就不确定
如果数据加强到10w
Tarjan缩点强联通分量DAG树上倍增
如果四票,仍然是至多一票不被满足,同上一种情况
建完图之后,如果一个提案的通过能走到它自己的否决,就必须选择否决,如果否决能走到通过,就必须选择通过。
否则就不确定
如果数据加强到10w
Tarjan缩点强联通分量DAG树上倍增

考虑把图变成树然后再做?
树是一个二分图(没有换,奇数深度点放左边,偶数角度点放右边)
图咋变成树?缩点,生成树
一张图如果不是二分图说明有基环,那么删去的边应该是所有基环的交集
先把这张图随便求一颗生成树,那么所有的边就可以分为树边和非树边。如果没有非树边的话就是二分图了,而这些非树边连接了两个同样颜色的点导致出现了基环。目标就是删掉这样的边使得所有的基环都被破坏掉
如果只有一条连接两个相同颜色节点的边,就说明只要删掉这个基环上面任何一条边
如果有两条及以上的非树边形成基环,那么不能删掉一条非树边来满足要求,所以删去的一定是树边,且被所有的基环所覆盖
如果一条边被一个基环所覆盖,就把这一个基环的边权值加一。最后只需要找被所有的基环经过的边就可以了
用数据结构维护。可以树上差分或者线段树,树剖


观察得A国必须是一奇一偶,所以最多两个人,枚举就行了
然后找出在B国的最大朋友圈
B国的朋友关系有什么性质?
B国的人可以分成奇数和偶数两部分,奇数的人互相是朋友,所有偶数互相是朋友
第二个条件就是在两个集合之间连边
二分图是左边没有连边,右边没有连边,中间有连边
那么这张图就是二分图的补图(有的边去掉,没有的加上)
或者说对它求一个补图就是二分图
求一个最大朋友圈,就是在补图上求一个最大独立集
如果最大匹配是x,那么最大独立集一定是x,n-x,m-x,n+m-x,n+m-2x中的一个
这个题是n+m-x
因为每有一对匹配,能选的点就会少一个,有x对就是少一个,所以是n+m-x,详细证明建最大流最小割定理

标签:表达式 观察 四种 设置 最大独立集 倍增 san lang min
原文地址:https://www.cnblogs.com/lcezych/p/11620415.html