标签:连通 建立 练习 范围 优先 枚举 lol 计划 子序列
单调栈,单调队列,优先队列。
Description
给你一堆数,有 \(n\) 个,并对他们操作 \(m\) 次。每次取出最大的一个数 \(x\),称之为母数。并将 \(x\) 分割成左端数 \([x \times p]\) 和右端数 \(x-[p \times x]\),并把这两个数放回数堆中,其余数均增加 \(q\) 。\(p\) 固定为 \((0,1)\) 的有理数。要求输出每次操作的数x和m次操作后所有数的和。
Solution
对于 $85% $ 的数据,是可以用优先队列搞的。我们用优先队列维护所有蚯蚓的长度,每次取出长度最长的蚯蚓,将其切成两半并丢回队列。有一个问题是如何让其他蚯蚓的长度增加 \(q\) 呢?可以记录蚯蚓整体增加的长度,对被切成两半的蚯蚓,将其长度 \(-q\) 即可。
对于 \(100\%\) 的数据,数据范围不允许带 \(log\),但是找规律可以发现一个隐藏的单调性,先切成两半的蚯蚓的一半一定别后切成两半的蚯蚓的对应一半长。所以可以用三个队列分别维护没有被切的蚯蚓,被切成 \([x \times p]\) 的蚯蚓,和被切成 \(x- [p \times x]\) 的蚯蚓,每次选出三个队列中最大的蚯蚓切一下再丢回对应队列中即可。
Description
有 \(n\) 块石头,排成一个环,第 \(i\) 块石头高度 \(a_i\),两块不同的石头 \(i,j\) 能够互相看到,当且仅当它们在环上的两条路径中有至少一条路径上,除了两个端点,路径上石头高度都不大于 \(min?(a_i,a_j)\)。求有多少对石头能互相看到。
Solution
首先考虑一个子问题,将原问题放在一条链上,且所有 \(a_i\) 都不相同。如果我们能处理出两个数组 \(L\) 和 \(R\),\(L_i\) 表示 \(i\) 左边第一个比它大的数,\(R_i\) 表示 \(i\) 右边第一个比它大的数。那么只需线性扫一遍,如果一个数前驱计数器 \(+1\),有后继计数器 \(+1\) 就可以了。那么问题在于如何求这两个数组呢?\(O(n^2)\) 暴力是会超时的,我们考虑用单调栈来搞定。维护一个单调递减的单调栈,从前往后遍历 \(a\)。假如当前遍历到了 \(a_i\),栈顶元素为 \(a_j\)。如果 \(a_i>a_j\),就将 \(a_j\) 弹出,一直到 \(a_i < a_j\) 时,将 \(a_i\) 压入栈并记录 \(L_i = a_j\)。同理,我们从后往前枚举,就可以求出 \(R\)。
将子问题扩展到 \(a_i\) 有相同的情况,若 \(a_i = a_j\),\((i,j)\) 可以互相看到,我们可以记录一个 \(sum\),\(sum_i\) 表示\([i,R_i - 1]\) 有多少个数 \(=a_i\),显然对于相等的情况我们不需要分出前驱和后继。进一步地,我们考虑将子问题扩展到环上,我们要求一个点,从这个点把环切成两半,但是这样会让我们的答案个数减少,所以我们还要用各种统计把答案加回来,现在选择哪个点切开最好呢?显然是切开最大的数,有多个的话切开任意一个。为什么?显而易见,除了 \((i,j)\) 中至少有一个最大数,没有任何一个其他的 \((i,j)\) 能通过这个最大数互相看到。所以最后我们 \(O(n)\) 扫一遍看看有多少个数可以和最大值互相看到就可以了。
路径压缩,按秩合并,带权并查集。
Description
动物王国中有三类动物 \(A,B,C\),\(A\) 吃 \(B\), \(B\) 吃 \(C\),\(C\) 吃 \(A\)。现有 \(N\) 个动物,以 \(1 \sim N\) 编号。每个动物都是 \(A,B,C\) 中的一种,但是我们并不知道它到底是哪一种。
一个人按顺序说了 \(K\) 句话,第一种说法是 1 X Y,表示 \(X\) 和 \(Y\) 是同类。第二种说法是 2 X Y,表示 \(X\)吃\(Y\)。但这 \(K\) 句话真假不明,当一句话满足下列任一条件,这句话就是假话,否则就是真话。
求假话的总数。
Solution
并查集能维护连通性、传递性。比如朋友的朋友是朋友,朋友的敌人是敌人。但是,维护敌人的敌人是朋友就很难维护了,所以就有种类并查集的诞生。这道题有三个物种,于是我们给并查集开三倍的空间。对于每种生物,第一倍空间储存同类,第二倍储存猎物,第三倍储存天敌,我们不能确定每种生物是 \(A\) 还是 \(B\) 还是 \(C\),知道生物的相对关系就够了。
讨论第一种话,\(X\) 与 \(Y\) 是同类,可以转换成 \(X\) 不吃 \(Y\) 且 \(Y\) 不吃 \(X\)。如果有一点不满足,那么就是谎言。如果都满足,那么 \(X\) 的同类都是 \(Y\) 的同类,\(X\) 的天敌都是 \(Y\) 的天敌,\(X\) 的猎物都是 \(Y\) 的猎物。再讨论第二种话,\(X\) 吃 \(Y\),可以转换成 \(X\) 与 \(Y\) 不是同类且 \(Y\) 不吃 \(X\)。如果有一点不满足,那么就是谎言。如皋港都满足,那么 \(X\) 的同类是 \(Y\) 的天敌,\(X\) 的天敌是 \(Y\) 的猎物,\(X\) 的猎物是 \(Y\) 的同类。
线段树合并,线段树懒标记,线段树维护。
树状数组求逆序对,最长单调子序列。
权值线段树,主席树。
Description
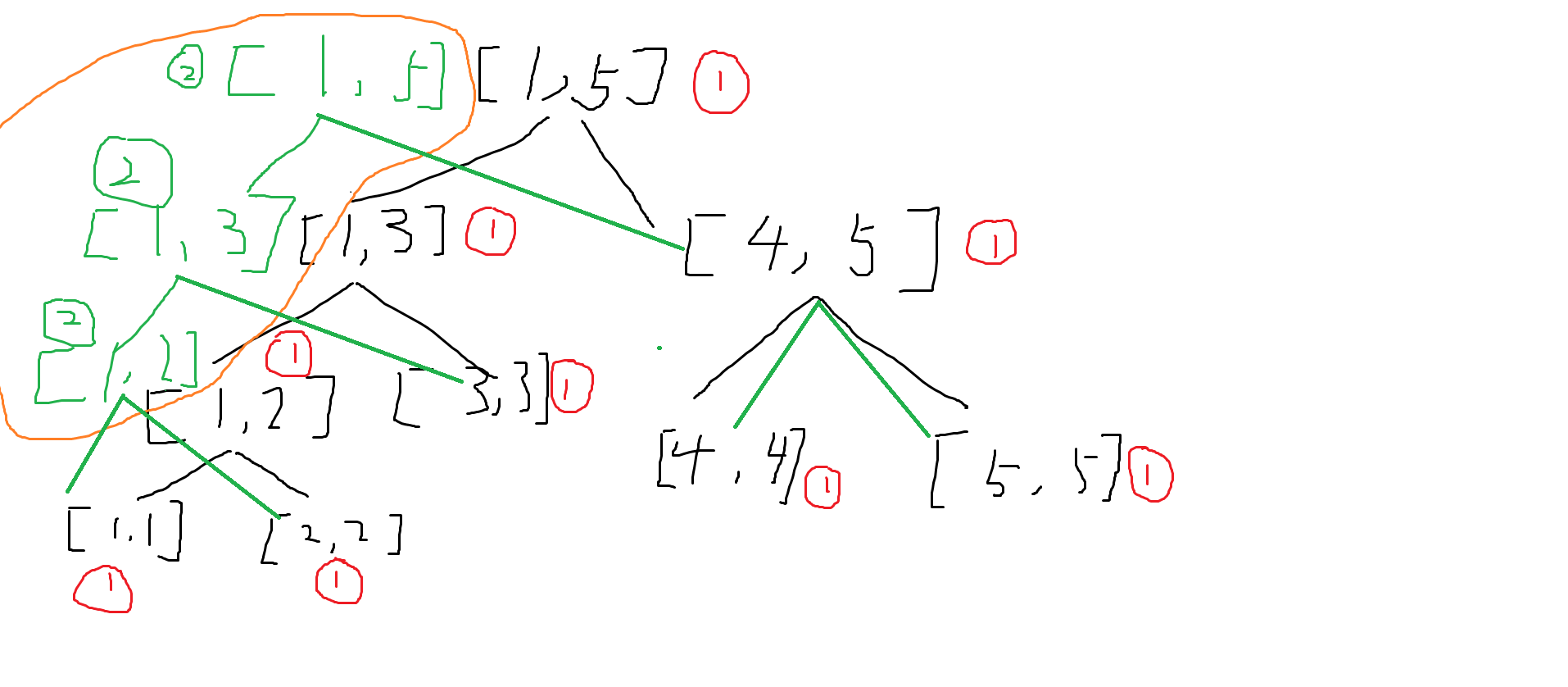
有 \(n\) 个城市,编号依次为 \(1\) 到 \(n\),它们之间计划修建 \(m\) 条双向道路,其中修建第 \(i\) 条道路的费用为 \(c_i\)。 有 \(q\) 次询问,每次询问选定一个区间 \([l, r]\) ,仅使用编号在该区间内的道路。他希望选择一些道路去修建,使得连通块的个数尽量少,同时,他不喜欢修建多余的道路,因此每个连通块都可以看成一棵树的结构。计算最小的费用。
Solution
先考虑暴力做法,就是将区间内的边扔进一个数组去跑 Kruskal。但是这个题的 \(n\) 极小,这意味着我们可以用线段树维护跑 Kruskal 可能用到的边,为 \(O((M + q)NlogM)\)。
Description
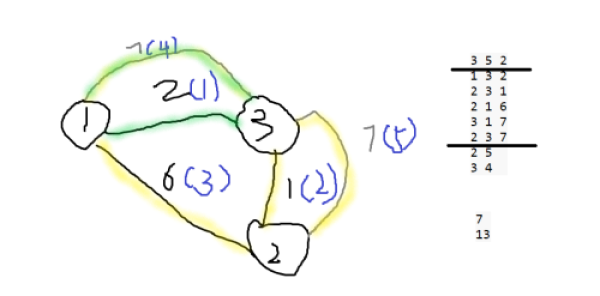
有一个长度为 \(n\) 的序列 \(f,f_i \in 1 \sim m\),有一个长度为 \(m\) 的价值序列 \(w\) 。选择一个区间 \([l,r]\) 获得的价值是
\[
\sum_{i=l}^r w_{f_i} \times [count(f_i)=1]
\]
问价值最大的区间的价值。
Solution
预处理出每个数在序列 \(f\) 中第一次的位置,和 \(f_i\) 在 \(f\) 中下一个出现的位置 \(nxt\)。用线段树维护每个位置作为右端点的答案。首先预处理出以 \(1\) 为左端点的答案。当 \(l + 1\) 时,\([l, nxt_i - 1]\) 间答案 \(-w_{f_l}\)。而 \([nxt_i, nxt_{nxt_i} - 1]\) 间答案 \(+w_{f_i}\)。如果 \(nxt\) 不存在,可以看作是 \(n + 1\)。然后每次更新最大值。
Description
给定一棵 \(N\) 个节点的树, 每个点 \(i\) 有权值 \(a_i\)。有 \(Q\) 个询问, 对于询问 \(x,y,k\) , 分别输出树上从 \(x\) 到 \(y\) 的路径中, 权值小于 / 等于 / 大于 \(k\) 的点的数目。强制在线。
Solution
这是对树的查询,我们可以通过求 \(lca\) 转换成对一条链的查询。套路地,对于一个点 \(x\),我们维护一个权值线段树以维护一个桶 \(b\),对于每一个在根到 \(x\) 路径上的点 \(y\),令 \(b_{a_y}++\)。当然,我们不能对每一个点重新建立一棵线段树,这个线段树要支持单点修改和区间求和,区间求和求的是前缀和。我们可以先 dfs? 一遍原来的树,在 dfs 的过程中建立主席树。
Description
有一个长度为 \(n\) 的数组 \(a_{1 \sim n}\)。\(m\) 次询问,每次询问一个区间内最小没有出现过的自然数。即求区间 mex。强制在线。
Solution
考虑建立权值线段树,维护每一个权值在原数组中最后一次出现的下标。对于查询操作 \([l,r]\) ,可以取出右端点所对应的主席树,并在树上二分查找下标小于 \(l\) 的最小权值即为答案。虽然 \(a_i\) 非常大,显然答案不会超过 \(n\),所以不用离散化。
咕咕。
标签:连通 建立 练习 范围 优先 枚举 lol 计划 子序列
原文地址:https://www.cnblogs.com/lyfoi/p/11620443.html