标签:class 最简 填充 研究 info tps style 维度 组合
https://news.cnblogs.com/n/641694/
9 月初,两名数学家借助计算机的力量,宣布他们终于解开了困扰了数学家 65 年之久的 42 的立方和之谜(详见:《42 之谜终于被破解了!》)。当时他们表示接下来他们最感兴趣的是数字 3 的非平凡解,但一个月不到,他们就找到想要的答案。而在更早的时候,另外两名数学家证明了一个跟有理数有关的猜想(详见:《困扰数学家近 80 年的无理数难题被证明了》)。我们很高兴看到这些数学进展,但同时又不免想起有些已经存在了数百年的数学问题,至今仍在挑战着人类的智慧。有的问题看起来很简单,但要证明它们却难如登天。下面,我们就要来看看几个这样的数学难题。
1. π+ e = ?
π和e是数学中最为人所知的两个常数,但是当把它们加起来时,却成了一个难倒众人的问题。
这个谜题与实代数数有关。一个实数如果是某个系数为整数的多项式的根,那么我们可以说这个实数是代数数。例如x²-6 是有着整数系数的多项式,因为 1 和-6 都是整数。x²-6 = 0 的根是 x = ±√6,这意味着√6 和-√6 都是代数数。所有有理数,以及有理数的根,都是代数数的。因此你可能会觉得,“大多数”实数都是代数数。然而结果却恰恰相反,“代数数”的反义词是“超越数”,事实证明几乎所有实数都是超越数。在这里,“几乎所有”是有数学含义的,那么哪些是代数数,哪些又是超越数?
π是一个已经存在了很久的实数,e大约在 17 世纪才为人所知。对于这样两个熟悉的数字,你可能会以为我们知晓与它们有关的任何基本问题。
事实是,我们知道π和e都是超越数的,但却不知道π + e 是代数数还是超越数。同样,我们不知道πe、π/e以及其他这两个数之间的简单组合是什么数。所以在数学中,还有着这样一些我们已经知晓了数百年甚至上千年的数字,蕴含着一些令人难以捉摸的基本问题。
2. γ是有理数吗?这是另一个写起来容易但解起来很困难的问题。你所要知道的一切就是有理数的定义。
有理数是可以被写成p/q形式的数字,其中p和q都为整数。所以 42、11/3,都是有理数;π和√2 是无理数。这是一个非常基本的性质,因此你或许会认为我们可以很轻易地判断出一个数字是否是有理数。
然而让我们来认识一下欧拉常数——γ。这是一个实数,约等于 0.5772,下图中的方程表示的就是γ的闭型。
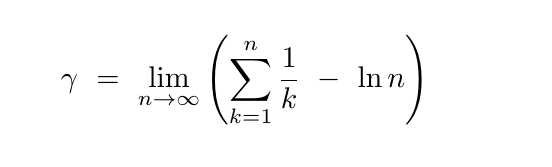
用文字来表达就是:“γ是调和级数与自然对数之差的极限。”所以说它是两个已经被理解得很好的数学对象的组合,它还可以用其他简洁的闭型表达,出现在数百个公式中。
但不知为何,我们偏偏不知道γ是否是有理数。我们对它的计算已经达到数千亿位数,但是仍然无法证明它的有理性。一种理论认为,γ是无理数。与上一个问题中的π+ e 很像的是,这是另一个我们无法回答关于一个熟悉数字的基本属性。
3. 吻接数问题

图片来源:JJ Harrison / Wikimedia Commons
数学中的一类广泛的问题,叫做球体填充问题。无论是在纯数学还是实际应用中都存在这些问题。在数学中它所涉及的问题是将球体堆积在给定的空间内,而在现实生活中的一个例子是杂货店里高高堆起的水果。这类问题的某一些已经有了完整的解决方案,而一些简单的问题却让我们困惑不解,比如吻接数问题。
当一堆球聚集在某个区域时,每个球都有一个吻接数,它表示的是与这个球接触到的其他球的数量。如果与某个球相邻的球体有 6 个,那么它的吻接数就是6。一堆球会有一个平均的吻接数,这个数字有助于我们用数学方法来描述这种情况。但是,一个与吻接数有关的基本问题,至今仍然没有得到解答。
首先,我们先要对维度作出一些说明。维度在数学中具有特定的含义:它们是独立的坐标轴。x轴和y轴表示坐标平面的两个维度。所以每当科幻电影中的角色说他们要去往一个不同的维度时,这些话在数学上是没有意义的,因为你无法“去往x轴”。
我们知道,一维是一条直线,二维是一个平面。对于这些较低的维度数值来说,数学家们已经证明这些维度中的球体可能存在的最大吻接数。在一维直线上是2——左右两边各一个。三维空间的确切吻接数直到上世纪 50 年代才得到证明。
三维之外的吻接数问题几乎没有得到解决。数学家们现在已慢慢地将可能性缩减到相当窄的范围——最多 24 个维度,其中一些维度的吻接数是已知的。对于较大的数或一般形式,这个问题的开放性还很大。在获得完整解决方案的道路上存在好几个重大的障碍,其中包括计算能力上的限制。因此,预计在未来几年,这一问题将能逐步取得进展。4. 解结问题

图片来源:Wikimedia Commons
解结问题中的最简单版本已经得到了解决,但还没能得到全面的解决。
这个问题与纽结理论有关,它的想法是试着运用正规的数学方法(例如证明)来打结(比如系鞋带)。
例如,你可能知道如何打一个“方型扭结”和“外平行结”。它们的打结步骤一样,只要将方型扭结的其中一个结朝相反的方向打就能得到一个外平行结。但是你能证明这些结是不同的吗?纽结理论便可以。


方型扭结(上)与外平行结(下)。 图片来源:Wikimedia Commons
扭结理论学家要处理的一个重大问题是研究一种算法,以确定一些混乱的纠缠是否是真正的扭结,还是说它可以解除纠缠。好消息是,数学家已经在过去的 20 年里成功编写出了这样的算法。
解结问题仍然是计算性的。它是一种NP(非确定性多项式)类问题,但我们却不知道它是否是一种P类问题。这意味着目前的情况是,我们已知这些算法能够处理具有任何复杂性的解结问题,但当它们变得越来越复杂时,处理这个问题的时间就会长到不可思议。
如果有人能提出一种算法,可以在所谓的多项式时间内解开任何一个结,那么解结问题就能得到彻底的解决。另外,如果有人可以证明这是不可能的,那么这意味着解结问题所面临的浩大的计算强度问题就是无可避免的。
5. 大基数问题

图片来源:Wikimedia Commons
19 世纪末,德国数学家格奥尔格·康托尔(Georg Cantor)发现无穷大是存在不同大小的,他证明了一些无限集合中所含有的元素比其他的无限集合更多。
最小的无限集合可以用ℵ?表示,这是自然数集合的大小,可以写成? =ℵ?。接下来是一些常见的比ℵ?更大的无限集合,比如康托尔证明了实数集比ℵ?更大,即? >ℵ?。但是实数集也并非那么大,这只是无限大的开始。
数学家们还在不断地发现越来越大的无穷大,或者我们可以称之为大基数。这是一个纯数学过程,如果有人说“我想到了基数的定义,我可以证明这个基数比所有已知的基数都大”,那么,如果他的证明是正确的,那这就会是已知最大的基数。直到有人想出一个更大的。
整个 20 世纪,大基数的疆域在不断向前推进,现在的维基百科里甚至有一个“基数”词条,里面有许多著名的基数都是以康托尔的名字命名的。那么,这一切会终结吗?答案几乎是肯定的,尽管它会变得非常复杂。
从某种意义上说,庞大的基数等级的顶端就在眼前。一些已被证明的定理对可能存在的基数提供了某种上限。但未知的问题仍有很多,最新的一些基数直到 2019 年才确定下来。未来几十年,我们很可能会发现更多基数。希望我们最终能获得一张所涵盖了有大基数的列表。
6. 哥德巴赫猜想
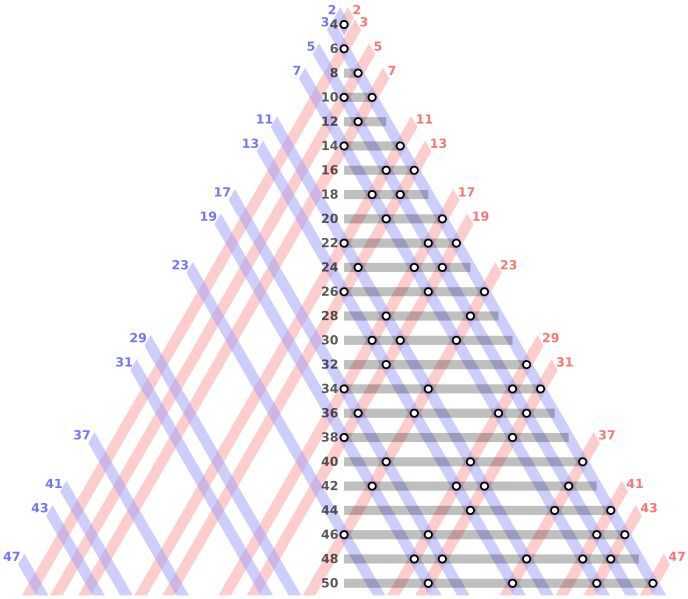
图片来源:Wikimedia Commons
在数学的众多未解之谜中,有些最困难的问题也有可能用简单的文字就能描述,例如哥德巴赫猜想,它说的是:“每一个大于 2 的偶数都是两个质数的和。”你可以在脑海中用较小的数字快速检查一下:18 = 13+5,42 = 23+19。计算机对这个猜想的验证已经扩展到了非常大的数量级,但即便如此,我们还是缺乏可以表明这对所有自然数都成立的证明。
哥德巴赫猜想源于 1742 年德国数学家克里斯蒂安·哥德巴赫(Christian Goldbach)和瑞士传奇数学家莱昂哈德·欧拉(Leonhard Euler)之间的信件,欧拉说:“我认为(它)是一个完全确定的定理,尽管我无法证明它。”或许欧拉已经察觉到是什么让这个问题如此难以解决。对于更大的数字,它们有更多的被写成两个质数之和的方式。就像 8 只能被拆分成 3 和 5 这两个质数的和,但是 42 可以分解成5+37、11+31、13+29、19+23。因此对于那些非常大的数字来说,哥德巴赫猜想仍是一个不充分陈述。直到现在,数学家仍无法证明完全证明哥德巴赫猜想,它是所有数学中最古老的开放式问题之一。
参考链接:https://www.popularmechanics.com/science/math/g29251596/impossible-math-problems/
标签:class 最简 填充 研究 info tps style 维度 组合
原文地址:https://www.cnblogs.com/jinanxiaolaohu/p/11616867.html