标签:sum amp 输出 day 有用 tarjan str 最短路 一个


T1
确定一个异构体在最优情况下传递的能量
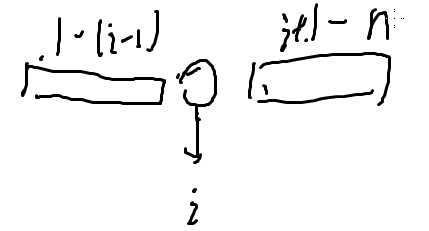
每一个都达到v
前缀和表示总能量
因为都要变成v,所以前i-1总能量应该是(i-1)*v
也就是说i不需要向左边输出能量
右边最后的能量值应该是(n-i)*v
节点的作用就是把左边的能量的差值全部转移到右边去,这个差值就是它传递的能量
枚举每一个节点
总共四种情况
1.左边多,右边少 2.左边少,右边多
3.左边多,右边多,说明i自己少 此时需要两边与期望能量差值的max
4.左边少,右边少,说明i自己多 此时需要两边与期望能量差值的和
然后取max就行了
#include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; const int maxn=100010; int n,z[maxn]; long long sum[maxn]; void read() { scanf("%d",&n); for (int a=1;a<=n;a++) scanf("%d",&z[a]); } long long work() { for (int a=1;a<=n;a++) sum[a] = sum[a-1]+z[a]; if (sum[n]%n) return -1; long long ans=0,v=sum[n]/n; for (int a=1;a<=n;a++) { long long l=sum[a-1]-1ll*(a-1)*v; long long r=sum[n]-sum[a]-1ll*(n-a)*v; if (l<0 && r<0) ans=max(ans,-l-r); ans=max(ans,max(abs(l),abs(r))); } return ans; } int main() { read(); printf("%lld\n",work()); return 0; }


T2
从左向右走?其实没啥用,答案和这个没有关系
可以把这些数从小到大排序,这样就只用考虑这个数是不是前边的数的倍数就行了
最长上升子序列
F[i]表示选择a[i]的情况下序列长度最长是多少
转移就是枚举它前面的数
只需要保证a[i]是a[j]的倍数就行了,因为a[j]一定已经是前边的数的倍数了
f[i]=max(f[j])+1 a[i]|a[j]
50pts
如果没有重复的
答案的长度不超过logn
那么就可以去重,因为只要一个重复的选上,其他就必须选
去重之后跑搜索也可以过
或者把dp在去重之后的数组上做,也可以过
正解?
所有的数<=10^6这个条件还没有用过
可以开10^6个桶记录每个数出现了多少次
用f[i]表示现在取出的序列在最后一个数为i的情况下最长有多长
现在取出的数是i,那么之后的都是i的倍数
f[k*i]=max(f[i]+cnt[k*i)
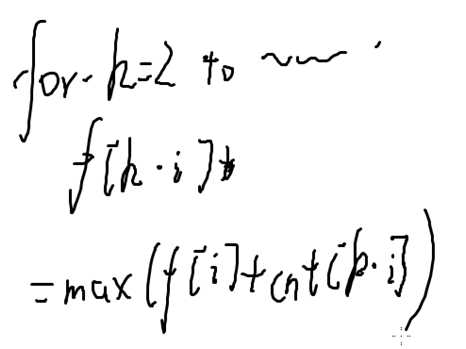
我们并不关心每个数是多少,只关心有多少个
#include<cstdio> #include<cstdlib> #include<cstring> using namespace std; const int maxn=1000010; int n,cnt[maxn],f[maxn]; int main() { scanf("%d",&n); for (int a=1;a<=n;a++) { int v; scanf("%d",&v); cnt[v]++; f[v]++; } int ans=0; for (int a=1;a<=1000000;a++) if (f[a]) { if (f[a]>ans) ans=f[a]; for (int b=a+a;b<=1000000;b+=a) if (cnt[b] && f[a]+cnt[b]>f[b]) f[b]=f[a]+cnt[b]; } printf("%d\n",ans); return 0; }


T3
2-SAT?
然鹅不会写
最小值最大化
二分
看看能否构造出战斗力大于等于v的卡牌组
现在有a1,b1和a2,b2
如果|a1-a2|,那么a1,a2不能同时选,从a1向b2连边
同理,从a2向b2连边
直接n^2枚举卡牌,然后跑2-SAT
50pts
不能过100pts的原因
原因:枚举建边是n^2的
60~70 pts 直接输出0 ??? 抽屉原理...我吐了
发现边太多了,我们想尽量节省边的数量
线段树优化建图(大雾)
把a1b1,a2b2...anbn拿出来从小到大排序
C1,c2,...,c2n
考虑ci,一定对应原来的某个数
两条边之间建边的条件是|ai-aj|<v
也就是ci前面一段和ci后面一段,是连续的区间
李姐为是区间加边的操作
线段树
如果第五个节点排好序之后是a2 如果有一个冲突的,一定和b2连边
那么在a2这个节点下面挂一个b2
区间加边
假如a3想对2-6之间的节点加边
2-6拆成[2,2],[3,4],[5,6]
从a3对这三个区间加边
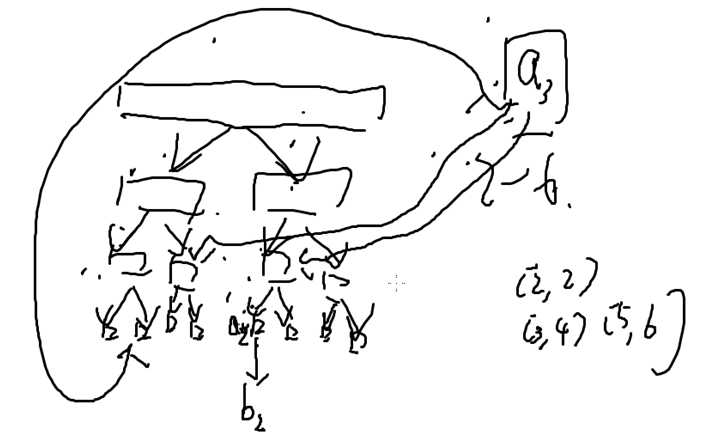
连通性没有发生改变
图和原来的是等价的
Zhxtql
所以边数是n log^2 n
然后跑tarjan
N 1,2,3,4...n
有m组边 第i组边是从i向li~ri连一个长度为di的边
求1~n的最短路
标签:sum amp 输出 day 有用 tarjan str 最短路 一个
原文地址:https://www.cnblogs.com/lcezych/p/11622280.html