标签:点积 题意 mic push ati cto 最大的 就会 问题
题意是给你一块在原点半径为10的圆,然后告诉你一条直线在圆弧上的极角,相当于用这条直线把这个圆分成两半,然后一共是n条直线切圆,就好比切蛋糕,问你其中最大一块的面积是多少。
如果我们将圆弧转化成直线边,那么这个题就变成PSLG裸题,但是这里是圆弧,所以我们需要将其转化。
我先将所有在圆上的点记录下来,最后极角排序,绕一周,这些点分割出来肯定会有一部分算面积的时候是要算上那部分弓型面积,但是有一部分不是,主要是这部分面积仅仅就是这块弓型面积,没有其他多边形面积,例如样例3,为了避免这种问题,我们可以直接在相邻两点之间塞入一个点,在进行连边,那么相当于我们给仅仅只有弓型区域内的点一个三角形面积,这样主要保证的是在跑PSLG的时候可以把这块面积算进去,因为每条边只算两次,但是如果是仅仅只有弓型面积所在的那条边,本来应该逆时针绕一圈算面积,所以这样就会有问题。
C++提交正确 G++wa惨???
这样就会有问题
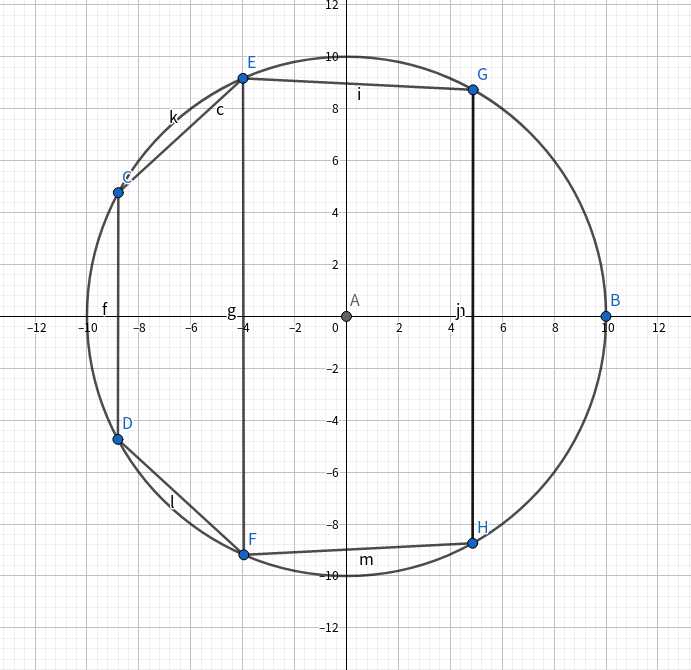
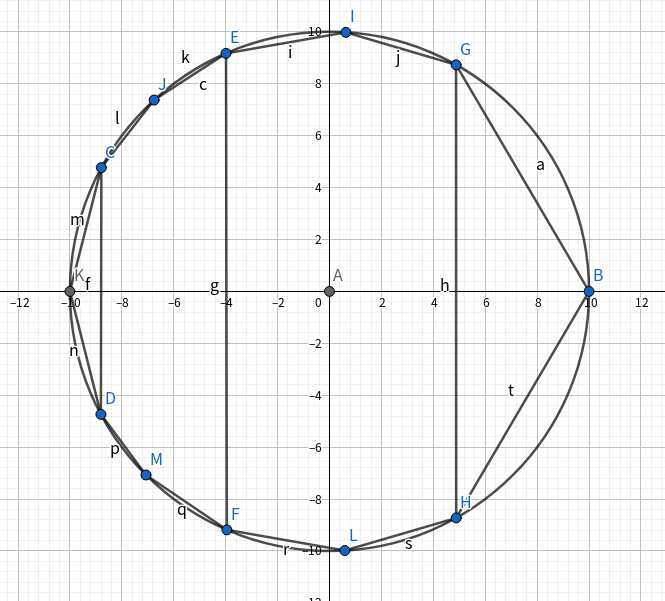
这样建边就没有大问题了
1 // ——By DD_BOND 2 3 //#include<bits/stdc++.h> 4 //#include<unordered_map> 5 //#include<unordered_set> 6 #include<functional> 7 #include<algorithm> 8 #include<iostream> 9 //#include<ext/rope> 10 #include<iomanip> 11 #include<climits> 12 #include<cstring> 13 #include<cstdlib> 14 #include<cstddef> 15 #include<cstdio> 16 #include<memory> 17 #include<vector> 18 #include<cctype> 19 #include<string> 20 #include<cmath> 21 #include<queue> 22 #include<deque> 23 #include<ctime> 24 #include<stack> 25 #include<map> 26 #include<set> 27 28 #define fi first 29 #define se second 30 #define pb push_back 31 #define MP make_pair 32 33 using namespace std; 34 35 typedef double db; 36 typedef long long ll; 37 typedef pair<db,db> Pd; 38 typedef pair<int,int> P; 39 typedef pair<ll,ll> Pll; 40 41 const db eps=1e-8; 42 const int MAXN=1e5+10; 43 const db pi=acos(-1.0); 44 const ll INF=0x3f3f3f3f3f3f3f3f; 45 46 inline int dcmp(db x){ 47 if(fabs(x)<eps) return 0; 48 return (x>0? 1: -1); 49 } 50 51 inline db Sqrt(db x){ 52 return x>0? sqrt(x): 0; 53 } 54 55 inline db sqr(db x){ return x*x; } 56 57 struct Point{ 58 db x,y; int id,nx; 59 Point(){ x=0,y=0; } 60 Point(db _x,db _y):x(_x),y(_y){} 61 void input(){ 62 double _x,_y; 63 scanf("%lf%lf",&_x,&_y); 64 x=_x,y=_y; 65 } 66 void output(){ printf("%.4f %.4f\n",(double)x,(double)y); } 67 bool operator ==(const Point &b)const{ 68 return (dcmp(x-b.x)==0&&dcmp(y-b.y)==0); 69 } 70 bool operator !=(const Point &b)const{ 71 return !((dcmp(x-b.x)==0&&dcmp(y-b.y)==0)); 72 } 73 bool operator <(const Point &b)const{ 74 return (dcmp(x-b.x)==0? dcmp(y-b.y)<0 : x<b.x); 75 } 76 db operator ^(const Point &b)const{ //叉积 77 return x*b.y-y*b.x; 78 } 79 db operator *(const Point &b)const{ //点积 80 return x*b.x+y*b.y; 81 } 82 Point operator +(const Point &b)const{ 83 return Point(x+b.x,y+b.y); 84 } 85 Point operator -(const Point &b)const{ 86 return Point(x-b.x,y-b.y); 87 } 88 Point operator *(db a){ 89 return Point(x*a,y*a); 90 } 91 Point operator /(db a){ 92 return Point(x/a,y/a); 93 } 94 db len2(){ //长度平方 95 return sqr(x)+sqr(y); 96 } 97 db len(){ //长度 98 return Sqrt(len2()); 99 } 100 db polar(){ //向量的极角 101 return atan2(y,x); //返回与x轴正向夹角(-pi~pi] 102 } 103 Point rotate_left(){ //逆时针旋转90度 104 return Point(-y,x); 105 } 106 Point rotate_right(){ //顺时针旋转90度 107 return Point(y,-x); 108 } 109 Point rotate(Point p,db ang){ //绕点p逆时针旋转ang度 110 Point v=(*this)-p; 111 db c=cos(ang),s=sin(ang); 112 return Point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c); 113 } 114 }; 115 116 inline db cross(Point a,Point b){ //叉积 117 return a.x*b.y-a.y*b.x; 118 } 119 120 inline db dot(Point a,Point b){ //点积 121 return a.x*b.x+a.y*b.y; 122 } 123 124 inline db dis(Point a,Point b){ //两点的距离 125 Point p=b-a; return p.len(); 126 } 127 128 inline db rad(Point a,Point b){ //两个向量的夹角 129 return fabs(atan2(fabs(cross(a,b)),dot(a,b))); 130 } 131 132 inline bool is_parallel(Point a,Point b){ //判断向量是否平行 133 db p=rad(a,b); 134 return dcmp(p)==0||dcmp(p-pi)==0; 135 } 136 137 struct Line{ 138 Point s,e; 139 Line(){} 140 Line(Point _s,Point _e):s(_s),e(_e){} //两点确定直线 141 Point operator &(const Line &b)const{ //求两直线交点 142 Point res=s; 143 db t=((s-b.s)^(b.s-b.e))/((s-e)^(b.s-b.e)); 144 res.x+=(e.x-s.x)*t; 145 res.y+=(e.y-s.y)*t; 146 return res; 147 } 148 }; 149 150 inline int relation(Point p,Line l){ //点和向量关系 1:左侧 2:右侧 3:在线上 151 int c=dcmp(cross(p-l.s,l.e-l.s)); 152 if(c<0) return 1; 153 else if(c>0) return 2; 154 else return 3; 155 } 156 157 inline bool is_parallel(Line a,Line b){ //直线平行 158 return is_parallel(a.e-a.s,b.e-b.s); 159 } 160 161 struct Circle{ 162 Point p; 163 db r; 164 Circle(){} 165 Circle(Point _p,db _r):p(_p),r(_r){} 166 }; 167 168 inline int relation(Point p,Circle a){ //点和圆的位置关系 0:圆外 1:圆上 2:圆内 169 db d=dis(p,a.p); 170 if(dcmp(d-a.r)==0) return 1; 171 return (dcmp(d-a.r)<0? 2: 0); 172 } 173 174 inline db area_radian(db th,db r){ //返回半径为R,弧度为th的弓形面积 175 return 0.5*r*r*(th-sin(th)); 176 } 177 178 inline db polygon_area(vector<Point> p){ //多边形的有向面积,加上绝对值就是面积 正值表示输入点按照逆时针 否则为顺时针 179 int n=p.size(); db area=0; 180 for(int i=1;i<n-1;i++) area+=cross(p[i]-p[0],p[i+1]-p[0]); 181 area=fabs(area)/2; 182 for(int i=0,j=1;i<n;i++,j++){ 183 if(j==n) j=0; 184 if(p[i].nx==p[j].id||p[j].nx==p[i].id) area+=area_radian(rad(p[i],p[j]),10); 185 } 186 return area; 187 } 188 189 struct Edge{ 190 int from,to; 191 db ang; 192 Edge(){ ang=from=to=0; } 193 Edge(int s,int t,db a){ from=s,to=t,ang=a; } 194 }; 195 int n,m,face_cnt; //平面个数 包括外面最大的多边形 196 db area[MAXN]; //每个多边形面积 197 Point point[MAXN]; //平面内所有的点 198 vector<Edge>edge; 199 vector<int>G[MAXN]; 200 vector<Point>polygon; 201 vector<Point>face[MAXN]; 202 int vis[2*MAXN],pre[2*MAXN]; //left表示这条边的左侧属于哪个面 203 inline void Init(){ 204 for(int i=0;i<(int)edge.size();i++) vis[i]=0; 205 edge.clear(); 206 for(int i=0;i<n;i++) G[i].clear(); 207 for(int i=0;i<face_cnt;i++) face[i].clear(); 208 n=m=face_cnt=0; 209 } 210 inline void AddEdge(int from, int to){ //需要建立反向边帮助寻找下一条边 211 edge.pb(Edge(from,to,(point[to]-point[from]).polar())); 212 edge.pb(Edge(to,from,(point[from]-point[to]).polar())); 213 m=edge.size(); 214 G[from].pb(m-2); 215 G[to].pb(m-1); 216 } 217 inline void Build(){ 218 for(int u=0;u<n;u++){ 219 int d=G[u].size(); 220 for(int i=0;i<d;i++) 221 for(int j=i+1;j<d;j++) 222 if(edge[G[u][i]].ang>edge[G[u][j]].ang) 223 swap(G[u][i],G[u][j]); 224 for(int i=0;i<d;i++) pre[G[u][(i+1)%d]]=G[u][i]; //从u出发的i条边顺时针旋转的第一条边是pre[i] 225 } 226 for(int u=0;u<n;u++){ 227 for(int i=0;i<(int)G[u].size();i++){ 228 int e=G[u][i]; 229 if(!vis[e]){ 230 while(1){ 231 vis[e]=1; 232 int from=edge[e].from; 233 polygon.pb(point[from]); 234 e=pre[e^1]; //逆时针旋转最多的一条边即为顺时针转动的第一条边 235 if(e==G[u][i]) break; 236 } 237 face[face_cnt++]=polygon; 238 polygon.clear(); 239 } 240 } 241 } 242 for(int i=0;i<face_cnt;i++) area[i]=polygon_area(face[i]); 243 } 244 245 typedef pair<Point,int> pdd; 246 247 pdd st[MAXN]; 248 vector<pair<db,int> >tmp[MAXN]; 249 250 inline bool cmp(pdd x,pdd y){ 251 return x.fi.polar()<y.fi.polar(); 252 } 253 254 inline void Insert(Line *line,int m){ 255 for(int i=0;i<m;i++) 256 for(int j=i+1;j<m;j++) 257 if(!is_parallel(line[i],line[j])){ 258 Point inter=line[i]&line[j]; 259 if(dcmp(inter.len()-10)>0) continue; 260 point[n++]=inter; 261 } 262 sort(point,point+n); 263 n=unique(point,point+n)-point; 264 for(int i=0;i<n;i++) point[i].id=i; 265 int cnt=0; 266 for(int i=0;i<n;i++) 267 if(dcmp(point[i].len()-10)==0) 268 st[cnt++]=pdd(point[i],i); 269 sort(st,st+cnt,cmp); 270 st[cnt]=st[0]; 271 for(int i=0;i<cnt;i++) st[i].fi.nx=st[i+1].fi.id; 272 for(int i=0;i<cnt;i++) point[st[i].se]=st[i].fi; 273 for(int i=0;i<m;i++){ 274 for(int j=0;j<n;j++) 275 if(relation(point[j],line[i])==3) 276 tmp[i].pb(MP(dot(point[j]-line[i].s,line[i].e-line[i].s),j)); 277 sort(tmp[i].begin(),tmp[i].end()); 278 for(int j=1;j<(int)tmp[i].size();j++) AddEdge(tmp[i][j-1].se,tmp[i][j].se); 279 } 280 for(int i=0;i<m;i++) tmp[i].clear(); 281 Build(); 282 } 283 284 typedef pair<db,Point> pd; 285 286 pd a[MAXN]; 287 Line line[MAXN]; 288 289 int main(void){ 290 int T; scanf("%d",&T); 291 while(T--){ 292 Init(); 293 int n,m=0,k=0; scanf("%d",&n); 294 for(int i=0;i<n;i++){ 295 double x,y; scanf("%lf%lf",&x,&y); 296 db s=x,t=y; 297 Point p1=Point(10*cos(s),10*sin(s)); 298 Point p2=Point(10*cos(t),10*sin(t)); 299 a[k++]=pd(s,p1); 300 a[k++]=pd(t,p2); 301 line[m++]=Line(p1,p2); 302 } 303 sort(a,a+k); 304 k=unique(a,a+k)-a; 305 a[k]=a[0]; a[k].fi+=2*pi; 306 for(int i=0;i<k;i++){ 307 Point tmp; 308 if(dcmp(a[i+1].fi-a[i].fi-pi)==0) tmp=a[i].se.rotate_left(); 309 else if(dcmp(a[i+1].fi-a[i].fi-pi)>0){ 310 tmp=a[i].se+a[i+1].se; 311 tmp=tmp/tmp.len()*-10; 312 } 313 else{ 314 tmp=a[i].se+a[i+1].se; 315 tmp=tmp/tmp.len()*10; 316 } 317 line[m++]=Line(a[i].se,tmp); 318 line[m++]=Line(tmp,a[i+1].se); 319 } 320 Insert(line,m); 321 sort(area,area+face_cnt); 322 printf("%.2f\n",(double)area[face_cnt-2]); 323 } 324 return 0; 325 }
标签:点积 题意 mic push ati cto 最大的 就会 问题
原文地址:https://www.cnblogs.com/dd-bond/p/11622309.html