标签:frame src amp bre i++ view ubi idt mat
定义
欧拉函数是 小于等于 x的数中与x 互质 的数的 数目
符号φ(x)
通式
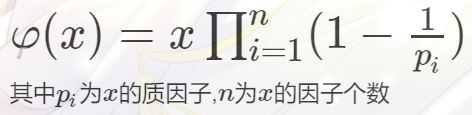
欧拉函数常用性质:
phy[i]=i-1 i为质数;
phy[i*j]={phy[i]*phy[j] i与j互质 (积性函数)
{=i*phy[j]=phy[i]*j i与j不互质
小于n的数中,与n互质的数的总和为φ(n)∗n/2 (n>1)φ(n)∗n/2 (n>1)
由上面的证明(更相减损术)我们知道,每一对与nn互质的数的和为nn,共有φ(n)/2φ(n)/2对
欧拉函数线性筛:
sushu[1]=1;phy[1]=1; for(int i=2;i<=n;i++) { if(!sushu[i]) { sushubiao[++q]=i; phy[i]=i-1; } for(int j=1;j<=q;j++) { if(sushubiao[j]*i<=500000) { sushu[sushubiao[j]*i]=1; if(gcd(sushubiao[j],i)==1) phy[sushubiao[j]*i]=phy[sushubiao[j]]*phy[i]; else phy[sushubiao[j]*i]=sushubiao[j]*phy[i]; } else break; } }
标签:frame src amp bre i++ view ubi idt mat
原文地址:https://www.cnblogs.com/oierjzy/p/11622308.html