标签:code class inline lin while view min 枚举 alc
csps模拟测试59
T2 Silhouette
神题
首先有一个很显然的性质:答案与a,b的顺序无关,这个很好证。
每个点有一个最大值,即点(i,j)为min(ai,bj)
手模一下样例可以发现,整张网格的最大值分成若干块,而块的数目不会超过2*n。
考虑在这些块上入手,容易发现块与块之间是互不影响的。
枚举每一块,又可以发现一个十分优秀的性质:这些块要么是矩形,要么是L形。
提取子问题:
给定一个a*b的矩形,矩形内每个数为[0,s],要求每一行每一列的最大值为s求方案数。
容斥,设f[i]表示至少i行不满足条件的方案数。
先选出i行,是一个C(a,i),
然后枚举每一列的情况,这一列中枚举的那i个位置是一定要不合法的,也就是只能在[0,s-1]中选,即s^i。
要保证这一列合法,另外a-i个位置一定要有一个s,(s+1)^(a-i)-s^(a-i)。
每一列都是这样,最后再直接^b即可
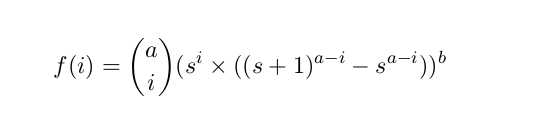
再考虑L形的情况,首先L形的只有可能是两个矩形的交汇处不合法(想一想为什么),我们在枚举的时候不合法的点只能在那个矩形里面选取
所以我们只需要把上式略微改一下就行了。
容斥一下就好了

1 #include<cstdio> 2 #include<algorithm> 3 #include<iostream> 4 #define int long long 5 using namespace std; 6 const int mod=1e9+7,N=1e5+5; 7 int a[N],b[N],n,js[N],js_inv[N],ans=1,tt[N<<1],tot; 8 inline int read() 9 { 10 int x=0;char c=getchar(); 11 while(c<‘0‘||c>‘9‘) c=getchar(); 12 while(c>=‘0‘&&c<=‘9‘) x=x*10+c-48,c=getchar(); 13 return x; 14 } 15 inline int C(int n,int m){return js[n]*js_inv[m]%mod*js_inv[n-m]%mod;} 16 inline int pow(int a,int b) 17 { 18 int ans=1; 19 for(;b;b>>=1,a=a*a%mod) if(b&1) ans=ans*a%mod; 20 return ans; 21 } 22 inline int calc(const int a,const int b,const int c,const int d,const int s) 23 { 24 int cnt=0; 25 for(register int i=0;i<=a;i++) 26 { 27 int sum=C(a,i)*pow(pow(s,i)%mod*((pow(s+1,a+c-i)-pow(s,a+c-i))%mod+mod)%mod,b)%mod*pow(pow(s,i)*pow(s+1,a-i)%mod,d)%mod; 28 if(i&1) (cnt-=sum)%=mod; 29 else (cnt+=sum)%=mod; 30 } 31 return (cnt%mod+mod)%mod; 32 } 33 inline void work() 34 { 35 register int i=n,j=n,lst1=n+1,lst2=n+1; 36 for(int k=tot;k;k--) 37 { 38 while(i&&a[i-1]==tt[k]) i--; 39 while(j&&b[j-1]==tt[k]) j--; 40 (ans*=calc(lst1-i,lst2-j,n-lst1+1,n-lst2+1,tt[k]))%=mod; 41 lst1=i,lst2=j; 42 } 43 } 44 signed main() 45 { 46 js[0]=1; 47 for(register int i=1;i<=N-5;i++) js[i]=js[i-1]*i%mod; 48 js_inv[N-5]=pow(js[N-5],mod-2); 49 for(register int i=N-6;i>=1;i--) js_inv[i]=js_inv[i+1]*(i+1)%mod; 50 js_inv[0]=1; 51 n=read(); 52 for(register int i=1;i<=n;i++) a[i]=read(),tt[++tot]=a[i]; 53 for(register int i=1;i<=n;i++) b[i]=read(),tt[++tot]=b[i]; 54 sort(tt+1,tt+tot+1);tot=unique(tt+1,tt+tot+1)-tt-1; 55 sort(a+1,a+n+1);sort(b+1,b+n+1); 56 if(a[n]^b[n]) return puts("0"),0; 57 work(); 58 printf("%lld\n",ans); 59 return 0; 60 }
标签:code class inline lin while view min 枚举 alc
原文地址:https://www.cnblogs.com/hzoi-kx/p/11622886.html