布隆过滤器理解

标签：垃圾邮件   直接   摘要   以太坊   大量   没有   com   bitmap   bit   

https://learnblockchain.cn/2019/04/30/bloom_filter/

可以理解为 对内容做多次摘要，把内容换成更小体积的标识位来存放。

要判断一个元素是不是在一个集合里，比较容易想到的方法是用数组，链表这样的数据结构把元素保存起来，然后依次比较来确定。

但是随着集合的变大，上面的这种方法就面临几个问题，首先比较的速度随着数据量的增加而变慢，其次存储集合的空间也越来越大。

为了解决上面的问题，就引入了布隆过滤器（Bloom Filter）

布隆过滤器原理

布隆过滤器的原理就是当一个元素被加入到集合的时候，用 K 个 Hash 函数将元素映射到一个位图中的 K 个点，并且把这个点的值设置为 1，在每次检索的时候我们看一下这个点是不是都是 1 就知道集合中有没有这个元素了。

这样说可能比较抽象，举个例子：

我们假设 K 是 2，有 Hash1 和 Hash2 两个哈希函数

1
2

Hash1 = n%3
Hash2 = n%8

然后我们创建一个名叫 bitMap 长度是 20 的位图

1

bitMap=[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

这个时候，我们要将 7，存入到这个集合中

1

n = 7

分别用 Hash1 和 Hash2 计算 n 哈希后的值

1
2

Hash1  ->  1
Hash2  ->  7

我们把 bitMap 对应的值置为 1，从 0 开始

1

bitMap=[0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

这样下次我们来查找 7 在不在这个集合的时候就可以用 Hash1 和 Hash2 计算完以后在 bitMap 集合中查找对应位置是否都是 1，如果都是 1 则一定在集合中。

如果再在集合中插入 13 分别用 Hash1 和 Hash2 计算 n 哈希后的值

1
2
3

n = 13
Hash1  ->  1
Hash2  ->  5

我们把 bitMap 对应的值置为 1，从 0 开始

1

bitMap=[0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

这个时候我们发现 1 被映射到了两次，但是并不影响我们在集合 [7, 13] 中快速找到 7 或者 13。

但是当插入的数据量大幅提升的时候，甚至 bitMap 全部被置为 1 的时候问题就很严重了，误识率就非常高了，这个也是根据不同场景实现布隆过滤器所要考虑的问题。

尽管有这样的问题，但是仍然不能掩盖布隆过滤器的空间利用率和查询时间远超其他算法，插入数据和查询数据的时间复杂度都是 O (k)

控制布隆过滤器的误判率

如果bit array集合的大小m相比于输入对象的个数过小，失误率就会变高。这里直接引入一个已经得到证明的公式，根据输入对象数量n和我们想要达到的误判率为p计算出布隆过滤器的大小m和哈希函数的个数k.
布隆过滤器的大小m公式:

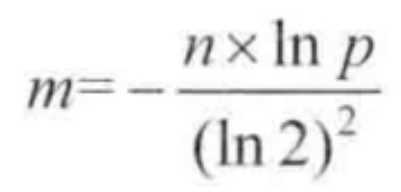
哈希函数的个数k公式:

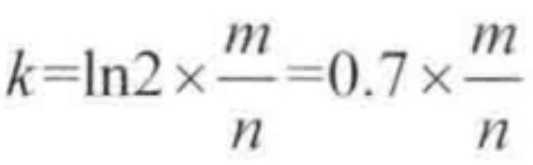
布隆过滤器真实失误率p公式：

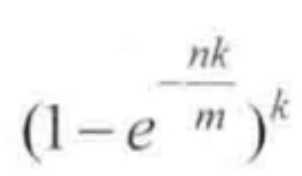
 假设我们的缓存系统，key为userId，value为user。如果我们有10亿个用户，规定失误率不能超过0.01%，通过计算器计算可得m=19.17n，向上取整为20n，也就是需要200亿个bit，换算之后所需内存大小就是2.3G。通过第二个公式可计算出所需哈希函数k=14.因为在计算m的时候用了向上取整，所以真是的误判率绝对小于等于0.01%。

应用场景

比较典型的应用场景就是检查垃圾邮箱的地址，比如我建立了一个垃圾邮件的布隆过滤器，当新邮件到来的时候我要快速的判断这封邮件是不是垃圾邮件。 还可以用来判断一个 URL 是不是恶意链接等等。 以太坊大量的用到了布隆过滤器，用来定位查找日志等。

布隆过滤器理解

标签：垃圾邮件   直接   摘要   以太坊   大量   没有   com   bitmap   bit   

原文地址：https://www.cnblogs.com/duoba/p/11623575.html