标签:c++ 技术 计算 不同 size 初始化 展示 names 输入
设有N堆石子排成一排,其编号为1,2,3,…,N。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这N堆石子合并成为一堆。
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
例如有4堆石子分别为 1 3 5 2, 我们可以先合并1、2堆,代价为4,得到4 5 2, 又合并 1,2堆,代价为9,得到9 2 ,再合并得到11,总代价为4+9+11=24;
如果第二步是先合并2,3堆,则代价为7,得到4 7,最后一次合并代价为11,总代价为4+7+11=22。
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
第一行一个数N表示石子的堆数N。
第二行N个数,表示每堆石子的质量(均不超过1000)。
输出一个整数,表示最小代价。
输入样例
4
1 3 5 2
输出
22
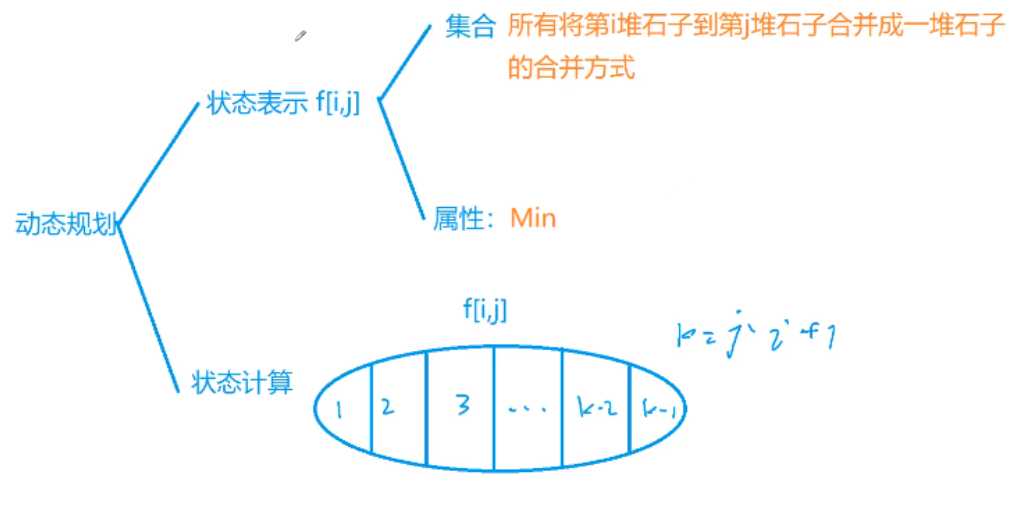
以该区间最后一次合并的时候,左边区间的数量来进行状态划分
max(f[i][k] + f[k+1][j] + s[j] - s[i - 1])
第一种方法
枚举开始位置与结束位置,注意状态计算的时候从下往上计算,即先计算f[n][n],注意比较最小值的时候,先赋值较大的数
#include<iostream> #include<algorithm> using namespace std; const int N = 300 + 10; int c[N], s[N], f[N][N]; int n; int main(){ cin >> n; for(int i = 1; i <= n; i ++){ cin >> c[i]; } for(int i = 1; i <= n; i++){ for(int j = 1; j <= i; j ++){ s[i] += c[j]; } } for(int i = n; i >= 1; i --){ for(int j = i; j <= n; j++){ if(i != j) f[i][j] = 1e9; for(int k = i ;k <= j - 1; k ++){ f[i][j] = min(f[i][k] + f[k + 1][j] + s[j] - s[i - 1], f[i][j]); } } } cout << f[1][n]; return 0; }
第二种方法
通过枚举区间的长度
#include<bits/stdc++.h> using namespace std; const int N=310,INF=0x3f3f3f3f; int f[N][N]; int s[N]; int n; int main(){ cin>>n; memset(f,INF,sizeof(f)); //记得初始化 for(int i=1;i<=n;i++){ cin>>s[i]; f[i][i]=0; //初始化 } for(int i=1;i<=n;i++) s[i]+=s[i-1]; for(int len=2;len<=n;len++){ for(int l=1;l+len-1<=n;l++){ int r=l+len-1; for(int k=l;k<r;k++){ f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]); } } } cout<<f[1][n]<<endl; return 0; }
标签:c++ 技术 计算 不同 size 初始化 展示 names 输入
原文地址:https://www.cnblogs.com/lurenjia712/p/11624493.html