标签:定义 邻接 out NPU 格式 print sed link sub
无向连通图 GG 有 nn 个点,n-1n−1 条边。点从 11 到 nn 依次编号,编号为 ii 的点的权值为 W_iWi?,每条边的长度均为 11。图上两点 (u, v)(u,v) 的距离定义为 uu 点到 vv 点的最短距离。对于图 GG 上的点对 (u, v)(u,v),若它们的距离为 22,则它们之间会产生W_v \times W_uWv?×Wu? 的联合权值。
请问图 GG 上所有可产生联合权值的有序点对中,联合权值最大的是多少?所有联合权值之和是多少?
第一行包含 11 个整数 nn。
接下来 n-1n−1 行,每行包含 22 个用空格隔开的正整数 u,vu,v,表示编号为 uu 和编号为 vv 的点之间有边相连。
最后 11 行,包含 nn 个正整数,每两个正整数之间用一个空格隔开,其中第 ii 个整数表示图 GG 上编号为 ii 的点的权值为 W_iWi?。
输出共 11 行,包含 22 个整数,之间用一个空格隔开,依次为图 GG 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大,输出它时要对1000710007取余。
5 1 2 2 3 3 4 4 5 1 5 2 3 10
20 74
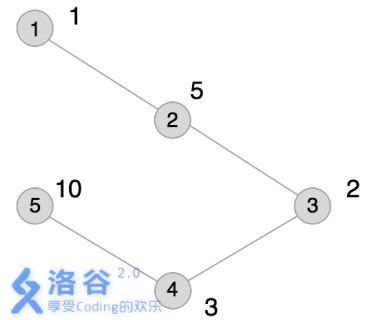
本例输入的图如上所示,距离为2 的有序点对有( 1,3)(1,3) 、( 2,4)(2,4) 、( 3,1)(3,1) 、( 3,5)(3,5)、( 4,2)(4,2) 、( 5,3)(5,3)。
其联合权值分别为2 、15、2 、20、15、20。其中最大的是20,总和为74。
【数据说明】
对于30%的数据,1 < n \leq 1001<n≤100;
对于60%的数据,1 < n \leq 20001<n≤2000;
对于100%的数据,1 < n \leq 200000, 0 < W_i \leq 100001<n≤200000,0<Wi?≤10000。
保证一定存在可产生联合权值的有序点对。
这一道题还是比较简单的
本蒟蒻在考场上做加强版的(距离为4)得了70分(T了3个点 太菜了)
拿到这上面来秒A!
这一道题是用O(n)的时间复杂度来实现的
就是我们所说的距离为二
仔细想想就是一个节点的两个儿子(就是和他相连的那些节点 这里就简称儿子吧)
我们只需要枚举每一个节点 把它的两个儿子相乘求和 并纪录最大即可
但是!
这一道题并没有规定有几个儿子
所以假如有3个儿子咋办?或者更多的儿子?
还是比较简单的 在有3个儿子的时候 我们所要求的就是2ab+2bc+2ab 那么这个式子可以变形为什么呢?
就是(a+b+c)^2-(a^2+b^2+c^2)神不神奇
也就是说针对每一个节点我们只需要记录一个和的平方 一个平方的和就行了
但是这一道题还要注意一下取模(考场上差点因为这个从70变成10)
就是你在用ans1*ans1%mod-ans2%mod的时候 可曾想过这会不会是一个负数 也就是说ans2>ans1*ans1 额。。
我们就这样:
((ans1*ans1%mod-ans2%mod)+mod)%mod
同时40分wa的小盆友们 注意题目只让对和取模偶 没有让对乘积的最大值取模
对了 仿佛还没有说最大乘积 这个也是非常的简单啊
就是也是在枚举每一个点的过程中 把它儿子里最大的和次大的记录下来 乘一下不就是了吗。。。(好无聊的问题)
下面上参差不齐的代码
#include<bits/stdc++.h> #define maxn 200005 #define mod 10007 using namespace std; vector<int> v[maxn]; int w[maxn]; int main() { int n;scanf("%d",&n); for(int i=1;i<n;i++){ int x,y; scanf("%d%d",&x,&y); v[x].push_back(y);v[y].push_back(x); } for(int i=1;i<=n;i++) scanf("%d",&w[i]); long long ans1=0,ans2=0,Maxans=-1,ans=0; for(int i=1;i<=n;i++){ long long Max=0,Sec=0; for(int j=0;j<v[i].size();j++){ ans1=(ans1+w[v[i][j]])%mod; ans2=(ans2+w[v[i][j]]*w[v[i][j]]%mod)%mod; if(w[v[i][j]]>Max) Sec=Max,Max=w[v[i][j]]; else if(w[v[i][j]]>Sec) Sec=w[v[i][j]]; } Maxans=max(Maxans,Max*Sec); ans=(ans+(ans1*ans1%mod-ans2%mod)%mod+mod)%mod; ans1=ans2=0; } printf("%lld %lld",Maxans,ans%mod); }

//link /* 首先这一道题的思路还是比较清晰的 就是说和的平方-平方的和 但是很难找出那些端点 怎么找端点呢? 我们可以枚举每一个节点! 这个节点的左儿子的儿子和右儿子的儿子相差4 那么我们再来理清一下思路 就是说枚举每一个节点 把它儿子的儿子们全都记上就行了 看起来好像很简单的样子耶 但是有一个前提 就是说你所枚举的那一个点必须有至少两个孙子 而且还不是同一个儿子生的。。 但是这样子说回来又不太对了。。 不对 上面的否决 偶 忽然想到了什么 要每一个当前枚举的节点的儿子的权值和去相乘 把每一个儿子的儿子们组合成一个整体。。。 偶! 那么倘若真的是这个样子 那么时间复杂度就是 O(nlogn)反正感觉这样子就 不会超时了 啊哈哈哈哈哈哈哈哈 前途一片光明! 只要俺把这一道题卡出来 就哈哈哈哈哈哈了 加油!还有2个小时 你能行! */ #include<bits/stdc++.h> #define maxn 200005 using namespace std; const long long mod=10007; int n; vector<int> v[maxn];//邻接表 int w[maxn]; inline int read() { int X=0; bool flag=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘) {if(ch==‘-‘) flag=0; ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘) {X=(X<<1)+(X<<3)+ch-‘0‘; ch=getchar();} if(flag) return X; return ~(X-1); } long long Get(int rt,int fa){//枚举孙子 求和 int y;long long Retans=0; for(int i=0;i<v[rt].size();i++){ y=v[rt][i];if(y!=fa) Retans=(Retans+w[y])%mod; } return Retans%mod; } int main() { freopen("link.in","r",stdin); freopen("link.out","w",stdout); scanf("%d",&n);int x,y; for(int i=1;i<=n-1;i++){ x=read(),y=read();//1.读入结束 v[x].push_back(y);v[y].push_back(x); } for(int i=1;i<=n;i++) w[i]=read(),w[i]%=mod; //2.开始枚举啊 long long ans1=0;//和的平方 long long ans2=0;//平方的和 for(int i=1;i<=n;i++){//枚举每一个中转点 long long ans11=0,ans22=0,t=0; if(v[i].size()>=2) for(int j=0;j<v[i].size();j++){//枚举儿子 long long AnsGrand=Get(v[i][j],i); if(AnsGrand!=0) t++; ans11=(ans11+AnsGrand)%mod; ans22=(ans22+AnsGrand*AnsGrand)%mod; } if(t>=1){ ans1=(ans1+ans11*ans11)%mod; ans2=(ans2+ans22)%mod;} } ans1%=mod; ans2%=mod; //ans1=(ans1*ans1)%mod; long long ans=((ans1-ans2)%mod+mod)%mod; printf("%lld",ans); return 0; }/* 8 1 2 1 3 3 4 4 5 4 6 6 7 7 8 8 2 6 7 9 3 2 10 1048 */
标签:定义 邻接 out NPU 格式 print sed link sub
原文地址:https://www.cnblogs.com/Tidoblogs/p/11625734.html