标签:png cstring ++ -- ide one closed lock a*
又炸了

T1 砖块
模拟
T2 数字
感谢rvalue学长的详细题解

问题是要从低位第一个非0位开始输出,所以就是$n! $除去所有的因子10(去掉后缀的0),即 $Ext(10,n!)$
而输出的数在k==1时是 $Ext(10,n!)\%10$,k==2时是$Ext(10,n!)\%100$, k==3时……
以10为例
而$\ %10$可以先求出$ \%2 $和$\ %5$的答案,在用CRT求最终的答案
$Ext(10,n!) \%2 $ 稍稍特判一下(一般都为0,但是小范围可能不是,所以小范围可以跑暴力)
$Ext(10,n!)\%5 $则需要把式子变一下
$$\begin{array}{rl}Ext(10,n!)&= \frac{n!}{10^{FP(10,n!)}}&= \frac{n!}{2^{FP(10,n!)}5^{FP(10,n!))}}&= \frac{n!}{2^{FP(5,n!)}5^{FP(5,n!)}}&=\frac{Ext(5,n!))}{2^{FP(5,n!)}}\end{array}$$
$FP(5,n!) $可以在$log_5^n $时间求出,那么$ 2^{FP(5,n!)} $的逆元就有了,只剩下$Ext(5,n!)$
$ Ext(k,n) $ 有性质 $Ext(ab,n)=Ext(a,n)*Ext(b,n) (a,b为质数)$
所以$$ \begin{array}{rl} Ext(5,n!)&= \prod\limits_{k=1}^{n} Ext(5,k) \\&=\prod\limits_{k\in[1,n],5|k} Ext(5,k)\times \prod\limits_{k\in[1,n],5\nmid k}Ext(5,k)\\&=Ext(5,(\frac{n}{5})!)\times \prod\limits_{k\in[1,n],5\nmid k}Ext(5,k)\\&=Ext(5,(\frac{n}{5})!)\times \prod\limits_{k\in[1,n],5\nmid k} k\end{array} $$
而 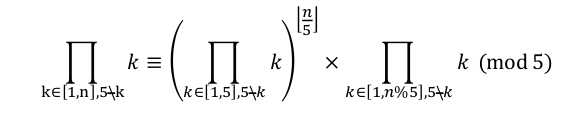
所以$$Ext(5,n!)= Ext(5,(\frac{n}{5})!) \times (\prod \limits_{k\in[1,5],5\nmid k} k)^{\lfloor \frac{n}{5} \rfloor} \times \prod \limits_{k\in[1,n\%5],5\nmid k} k (mod 5) $$
最终求出来 $Ext(5,n!)$ 乘上前面求的 $ 2^{FP(5,n!)} $的逆元 于是求出了$Ext(10,n!)\%5 $
和$Ext(10,n!)\%2 $ 跑CRT(大神都不用真的CRT)得出 $Ext(10,n!)\%10$的解
k==2和k==3同理
再以k==3 为例
$$Ext(5,n!)= Ext(5,(\frac{n}{5})!) \times (\prod \limits_{k\in[1,125],5\nmid k} k)^{\lfloor \frac{n}{125} \rfloor} \times \prod \limits_{k\in[1,n\%125],5\nmid k} k (mod 125) $$
最后一波福利(代码)

#include<iostream> #include<cstdio> #include<cstring> using namespace std; int T,k,a[110],FP[110],b[110],fac[150]; long long ans[11000]; int c[5],p[5],phi; inline void read(){ register char r; while(r=getchar(),r<‘0‘||r>‘9‘); a[0]=0; a[++a[0]]=r^48; while(r=getchar(),r>=‘0‘&&r<=‘9‘) a[++a[0]]=r^48; } long long qpow(long long a,long long b,long long mod){ long long ans=1; while(b){ if(b&1) ans=ans*a%mod; b>>=1; a=a*a%mod; } return ans; } int div(int a[],int b){ int tmp=0; for(register int i=a[0];i;i--){ tmp=tmp*10+a[i]; a[i]=tmp/b,tmp%=b; } while(a[a[0]]==0&&a[0]>=1) a[0]--; return tmp; } void jia(int a[],int b[]){ int tmp=0; for(register int i=1;i<=max(a[0],b[0]);i++){ tmp=a[i]+b[i]+tmp; b[i]=tmp%10; tmp/=10; } b[0]=max(a[0],b[0]); while(tmp) b[++b[0]]=tmp%10,tmp/=10; } int MOD(int a[],int mod){ return div(a,mod); } int work_FP(){ memset(FP,0,sizeof(FP)); memcpy(b,a,sizeof(b)); while(b[0]){ div(b,5); jia(b,FP); } return MOD(FP,phi); } void work_to_2(){ if(k==1) p[1]=2,p[2]=5,phi=4; else if(k==2) p[1]=4,p[2]=25,phi=20; else if(k==3) p[1]=8,p[2]=125,phi=100; if(a[0]>1) c[1]=0; else{ c[1]=1; for(register int i=1;i<=a[1];i++) c[1]=c[1]*i%p[1]; } } void work_to_5(){ int w=work_FP()+phi; w=qpow(qpow(2,w,p[2]),phi-1,p[2]); fac[0]=1; for(register int i=1;i<=p[2];i++){ fac[i]=fac[i-1]; if(i%5!=0) fac[i]=fac[i]*i%p[2]; } c[2]=1; while(a[0]){ memcpy(b,a,sizeof(b)); memset(FP,0,sizeof(FP)); div(a,5); c[2]=c[2]*fac[div(b,p[2])]%p[2]; jia(b,FP); c[2]=c[2]*qpow(fac[p[2]],MOD(FP,phi),p[2])%p[2]; } c[2]=c[2]*w%p[2]; } void work(){ for(register int i=a[0];i>=1;i--) b[++b[0]]=a[i]; memcpy(a,b,sizeof(a)); work_to_2(); work_to_5(); } void exgcd(int a,int b,int &x,int &y){ if(!b){ x=1; y=0; return; } exgcd(b,a%b,x,y); int t=y; y=x-a/b*y; x=t; return; } int CRT(){ int sum=p[1]*p[2]; int ans=0; for(register int i=1;i<=2;i++){ int a=sum/p[i],x,y; exgcd(a,p[i],x,y); ans=(ans+a*x*c[i]%sum)%sum; } return (ans%sum+sum)%sum; } void out(int x){ if(k==1) printf("%d\n",x%10); if(k==2) printf("%d%d\n",(x/10)%10,x%10); if(k==3) printf("%d%d%d\n",(x/100)%10,(x/10)%10,x%10); } int main(){ //freopen("3.out","w",stdout); scanf("%d",&T); ans[0]=1; for(register int i=1;i<=10000;i++){ ans[i]=ans[i-1]*i; while(ans[i]%10==0) ans[i]/=10; ans[i]%=((int)1e8); } while(T--){ read(); scanf("%d",&k); if(a[0]<=4){ int n=0; for(register int i=1;i<=a[0];i++) n=n*10+a[i]; out(ans[n]); } else{ work(); out(CRT()); } } }
T3 甜圈
要求完成的任务必须按顺序而且只能做一次,用hash表示状态
将甜圈编号作为线段树下标,经典的线段树操作就可以了
标签:png cstring ++ -- ide one closed lock a*
原文地址:https://www.cnblogs.com/heoitys/p/11626928.html