标签:image product 输出 算法实现 ota 拓扑序 特殊 ant sort
定义:
- 自反性(reflexive)
- 反对称性(antisymmetric)
- 传递性(transtive)
NOTE: R记作?,注意这里的?不必是指一般意义上的“小于或等于”,
若有x?y,我们也说x排在y前面(x precedes y.

- 如果(A, ≤)是一个偏序集(poset),那么对于其中的元素a和b,
- a≤b 或者 b≤a,那么称为可比的(Comparable)
- 即不存在a≤b,也不存在b≤a,那么称为不可比的(Imcomparable)
如果偏序集A中每对元素(every pair of elements)都是可比的,那么我们就称A是线序集合(linearly ordered set)或全序集合(totally ordered set),称偏序关系R为线序或全序关系(linear order). 我们也称A为链(chain).
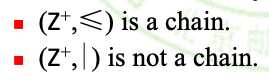
定义:
设集合(S,≤)为一全序集,≤是其全序关系,若对任意的S的非空子集,在其序下都有最小元素,则称≤为良序关系,(S,≤)为良序集。

定义:定义在A上的关系R是拟序关系iff其具有以下关系
- 自反性(reflexive)
- 传递性(transitive)
NOTE:满足反对称性的拟序关系就称为偏序关系
如果(A, ≤)和(B, ≤)都是偏序集,那么他们的笛卡尔积也是个偏序集,其偏序关系≤被定义为:
- 如果在A中有a ≤ a‘,在B中有b ≤ b‘,那么(a, b) ≤ (a‘, b‘)
对于一个乘积偏序,
(a, b) < (a‘, b‘)在a < a‘(或a == a‘并且b < b‘)时成立
那么我们称其为词典顺序(Lexicographic Order)或字典序(“dictionary” order)
- 删除了所有的自环(self-cycles)
- 消除了由传递性生成的边
- 自底向上的制图
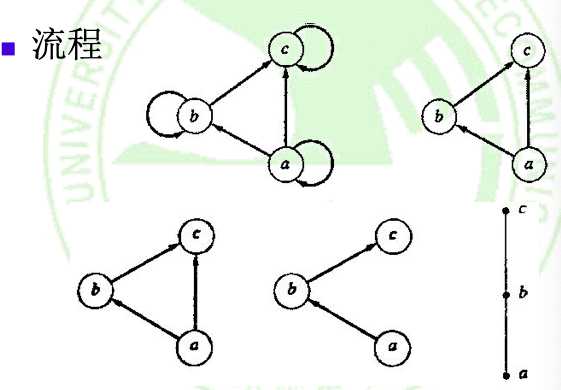


两个有限同构偏序集必定具有相同的Hasse图.
定义:
偏序集中的一个元素称为极大(小)元,当它不小(大)于这个偏序集中的任何其他元素, 利用哈斯图很容易判别它们就是图中的"顶"("底")元素
极大(小)元一定存在,且可能是不唯一的
定义:
如果在偏序集中存在一个元素大(小)于任何其他的元素,那么称这样的元素为最大(小)元
最大(小)元可能不存在,若存在则唯一
定义:
如果存在一个元素u(l)∈S,使得对于偏序集(S, ≤)的子集A中的所有元素a,有a?u(l?a),那么称u(l)为A的一个上(下)界,如果u(l)是所有上(下)界中最小(大)的,就叫最小上界(LUB)(最大下界(GLB))
上界的最小元就叫最小上界;下界的最大元叫最大下界
定义:
对一个有向无环图DAG(Directed Acyclic Graph)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序
NOTE:有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说
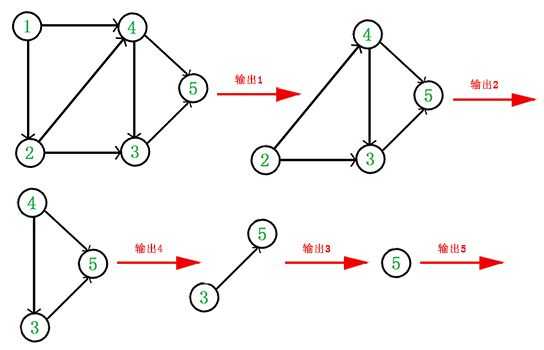
输出一个拓扑序列的常用算法实现:
- 从 DAG 图中选择一个没有前驱(即入度为0的顶点)并输出。
- 从图中删除该顶点和所有以它为起点的有向边并更新其他点的入度。
- 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。
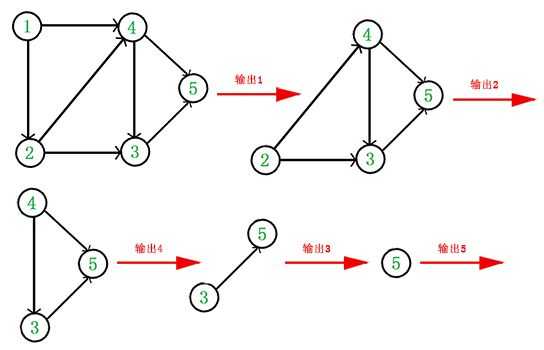
于是,得到拓扑排序后的结果是 { 1, 2, 4, 3, 5 }.
- 通常,一个有向无环图可以有一个或多个拓扑排序序列.
- 每次在入度为0的集合中取顶点,并没有特殊的取出规则,所以得到的拓扑排序也是随机的,如果对取出顶点顺序有要求,可以用优先队列.
- 我们可以通过对一个有向图进行拓扑排序,来判断是否存在环(存在拓扑序列则无环,不存在则有环)
定义:
如果一个偏序集的每对元素都有最小上界和最大上界,那么就称这个偏序集为格
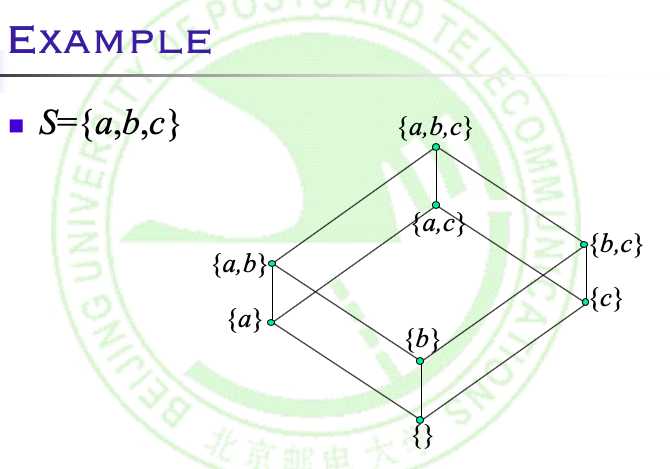
定理:两个格的笛卡尔乘积也是格
标签:image product 输出 算法实现 ota 拓扑序 特殊 ant sort
原文地址:https://www.cnblogs.com/SpicyArticle/p/11628963.html