标签:class line 初始 大于 quick swa 开始 算法 扫描
一 、递归 :直接或间接地调用自身的算法
整数划分问题
正整数 n 表示成一系列正整数之和,n=n1+n2+……+nk (n1 ≥ n2 ≥ …… ≥ nk ≥ 1,k ≥ 1),正整数 n 的这种表示称为正整数 n 的划分。正整数 n 的不同划分个数称为正整数 n 的划分数,记为 p(n)
正整数 6 有 11 种不同划分,p(6)=11
递归 --- > 在正整数 n 的所有划分中,将最大加数 n1 不大于 m 的划分个数记作q(n,m) 可以建立 q(n,m) 的如下递归关系
① q(n,n)=1 + q( n,n - 1)
② q(n,1) = 1 q(1,m) =1
③ q(n,m) { =m / <m
n = m+n2+……+nk Ⅰ (可见 m ≥ n2) Ⅰ 式中 m 左移 得到 Ⅱ式
n - m = n2+……+nk Ⅱ 即 q(n-m,m)
例
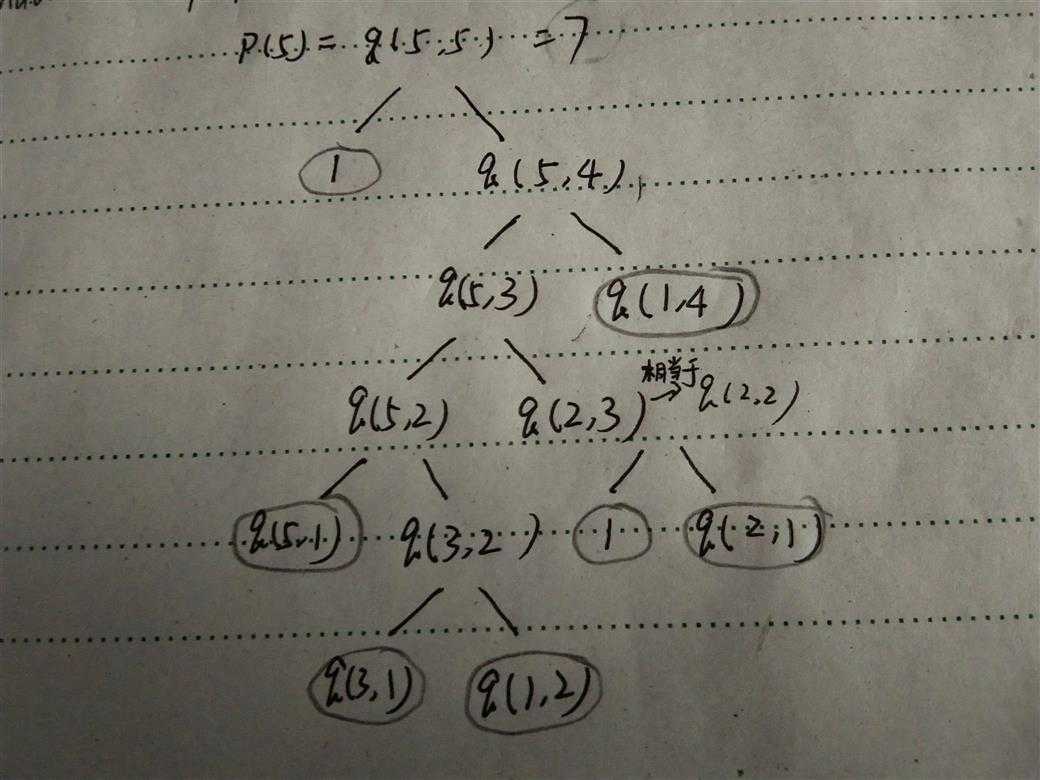
二、分治:将规模为 n 的问题分解为 k 个规模较小的子问题,这些子问题互相独立且与原问题相同。递归地解这些子问题,然后将各子问题的解合并得到原问题的解
使子问题的规模大致相同,即将一个问题分成大小相等的 k 个子问题,许多问题可以使 k = 2,这种使子问题规模大致相等的做法出自平衡子问题的思想,几乎总比子问题规模不等的做法要好
二分搜索 最坏情况时间复杂度:O(log n)
基本思想:将n个元素分成个数大致相同的两半,取 a[n/2] 与 x 进行比较。若 x=a[n/2],则找到x,算法终止;若x<a[n/2],则在数组a的左半部继续搜索x;若x>a[n/2],则在数组a的右半部继续搜索x
int BinarySearch(Type a[],const Type& x,int n) //找到x时返回其在数组中的位置,否则返回-1 { int left=0,right=n-1; while(left<=right) { int middle=(left+right)/2; if(x==a[middle]) return middle; if(x>a[middle]) left=middle+1; else right=middle-1; } return -1; //未找到x }
三、快排
基于分治策略的另一个排序算法,基本思想:对于输入的数组 a[p:r],按照以下三个步骤排序
①分解:以a[p]为基准元素,将 a[p:r] 分成 a[p:q-1],a[q] 和 a[q+1:r]。使a[p:q-1]中任何一个元素小于等于a[q],而a[q+1:r]中任何一个元素大于等于a[q]。下标q在划分过程中确定。(即每次都可以确定一个 元素a[q]的最终位置)
②递归求解:递归调用快排,分别对 a[p:q-1] 和 a[q+1:r] 进行排序
③合并:由于对 a[p:q-1] 和 a[q+1:r] 的排序就地进行,因此 a[p:q-1] 和 a[q+1:r] 都排好序后,无需计算,a[p:r]已经排好序
快排:
void QuickSort(Type a[],int p,int r) { if(p<r) { int q=Partition(a,p,r); QuickSort(a, p, q-1); //对左半段排序 QuickSort(a, q+1, r); //对右半段排序 } }
上述算法中函数Partition()以一个确定的基准元素a[p]对子数组a[p:r]进行划分,这是快排算法的关键
int Partition(Type a[],int p,int r) // O(n):每个元素扫描一次 { int i=p,j=r+1; //*** Type x=a[p]; while(true) //将小于x的元素交换到左边区域,将大于x的元素交换到右边区域 { while(a[++i]<x && i<r); //***若x为最大值,一直++i,越界,所以要 && i<r while(a[--j]>x); //***到a[p]时,遇到x,a[--j]<=a[p],不越界 if(i>=j) break; Swap(a[i],a[j]); } a[p]=a[j]; a[j]=x; return j; }
Partition 对a[p:r]进行划分,以元素a[p]作为划分的基准,分别从左、右两端开始,扩展两个区域a[p:r]和a[j:r],使a[p:i]中的元素小于或等于x,而a[j:r]中的元素大于或等于x。初始时,i=p, j=r+1
四、线性时间的选择
①将n个输入元素划分成 n/5 个组,每个组5个元素,出可能有一个组不是5个元素外。用任意一种排序算法,将每组中的元素排好序,并取出每组的中位数,共 n/5 个
②递归调用Select找出这 n/5 个元素的中位数。如果 n/5 是偶数,就找出它的两个中位数中较大的一个。然后以这个元素作为划分基准
标签:class line 初始 大于 quick swa 开始 算法 扫描
原文地址:https://www.cnblogs.com/C-ch3-5/p/11519567.html