标签:int inline image lin 图片 tor 决定 表示 代码
题意:
有一棵棵提米树,满足这样的性质:
每个点上长了一定数量的Temmie 薄片,薄片数量记为这个点的权值,这些点被标记为 1 到 n 的整数,其
中 1 号点是树的根,没有孩子的点是树上的叶子。
定义\((a,b)\)是一对相邻的叶子,当且仅当没有其它的叶子节点在 DFS 序上在a,b 之间。
每对相邻的叶子都会产生一个代价,代价为 a 到 b 路径上(不包含 a,b)的点中,最大点权值。
提米树可以提供决心,一棵提米树能提供的决心的数量是树上所有叶子上长的 Temmie 薄片数量和,减去所有相邻叶子的代价。
Temmie 们决定对这棵树进行若干次剪枝(可以不剪枝),使得这棵树能提供的决心最多。
一次剪枝定义为:如果一个点的孩子都是叶子,就可以把它所有的孩子剪掉。
要求\(O(n)\)做法。
首先,考虑\(O(n^2)\)的60分暴力:
我们可以反过来:由根开始,每个节点考虑是否扩展出所有叶子。
若不扩展,则它的子树都是空的,它成为叶子。
我们可以在dfs序上DP:设\(dp(i,j)\)表示考虑到i,上一个叶子点为j的最大决心。
有两种转移:
1、若i不是叶子,可以扩展,转移到\(dp(i+1,j)\)。
2、可以不扩展,转移到\(dp(i+si_i,i)+w_i-max(i,j)\)。
代码如下:
for(int i=tm-1;i>=0;i--)
{
for(int j=0;j<=n;j++)
{
int u=xl[i];
dp[i][j]=dp[i+si[u]][u]+sz[u]-zd[j][u];
if(si[u]>1&&dp[i+1][j]>dp[i][j])
dp[i][j]=dp[i+1][j];
}
}
printf("%d",dp[0][0]);考虑优化:首先,要把维度降下来。
设\(dp(i)\)表示i成为叶子后的最大决心。
枚举下一个使用2转移的位置,代码如下:
for(int i=tm;i>=0;i--)
{
int u=xl[i];
dp[i]=-999999999;
for(int j=i+si[u];j<=tm+1;j++)
{
int t=dp[j]-zd[u][xl[j]];
if(t>=dp[i])
dp[i]=t;
if(si[xl[j]]==1)//注意此处,非常关键。
break;
}
dp[i]+=sz[u];
}
printf("%d",dp[0]);继续优化:
我们发现,对于\(i\),\(i+si_i\)就是i的祖先节点中第一个有更右子节点的点。
而由于注释处的break,使得转移就是在\(i+si[u]\)处,一直向左走形成的链。
那么:
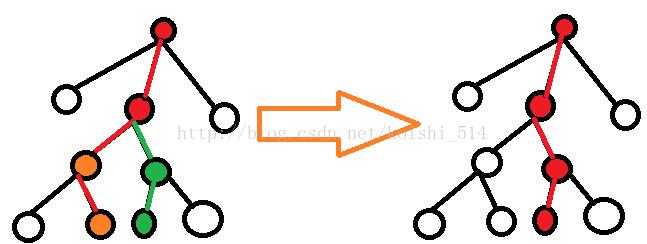
绿点对橙点有贡献。
那么,我们枚举红点lca,再枚举相邻的两个儿子,计算贡献。
先算出链上每个节点到lca的最大值。设为\(h\),那么,就是\(dp(u)=max(dp(v)-max(h(u),h(v)))+w(u)\)。
由于h具有单调性,因此分\(h(u)>h(v)\)和\(h(u)<=h(v)\)进行讨论,提前算出链上\(dp\),以及\(dp-h\)的最大值。
这两种情况符合的v一定是前缀/后缀,双指针扫一下即可定位。
代码细节非常多。
#include <stdio.h>
#include <vector>
#define inf 999999999
using namespace std;
vector<int> ve[100010];
int sz[100010],cl[100010],cr[100010],dp[100010],zd[100010],fa[100010],ma[100010],md[100010];
int max(int a,int b)
{
return a>b?a:b;
}
void dfs0(int u,int f)
{
fa[u]=f;
for(int i=0;i<ve[u].size();i++)
dfs0(ve[u][i],u);
}
void dfs1(int u)
{
for(int i=ve[u].size()-2;i>=0;i--)
{
dfs1(ve[u][i+1]);
int t=ve[u][i],la=0;zd[u]=sz[u];
while(t!=0)
{
zd[t]=max(sz[t],zd[fa[t]]);
t=cr[t];
}
t=ve[u][i+1];
while(t!=0)
{
zd[t]=max(sz[t],zd[fa[t]]);
la=t;t=cl[t];
}
t=la;while(t!=u)
{
ma[t]=dp[t]-zd[fa[t]];
if(cl[t])ma[t]=max(ma[t],ma[cl[t]]);
t=fa[t];
}
t=ve[u][i+1];
while(t!=0)
{
md[t]=dp[t];
if(fa[t]!=u)md[t]=max(md[t],md[fa[t]]);
t=cl[t];
}
ma[u]=md[u]=-inf;
int x=ve[u][i],y=ve[u][i+1];
while(x!=0)
{
while(y!=0&&zd[fa[y]]<zd[fa[x]])
y=cl[y];
if(y)
{
t=ma[y]+sz[x];
if(t>dp[x])dp[x]=t;
}
t=md[(y==0?la:fa[y])]-zd[fa[x]]+sz[x];
if(t>dp[x])dp[x]=t;x=cr[x];
}
}
if(ve[u].size())dfs1(cl[u]);
}
int main()
{
freopen("temmie.in","r",stdin);
freopen("temmie.out","w",stdout);
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int s,a;
scanf("%d%d",&sz[i],&s);
for(int j=0;j<s;j++)
{
scanf("%d",&a);
ve[i].push_back(a);
}
if(s>0)
{
cl[i]=ve[i][0];
cr[i]=ve[i][s-1];
}
dp[i]=-inf;
}
int u=1;
while(u!=0)
{
dp[u]=sz[u];
u=cr[u];
}
dfs0(1,0);dfs1(1);
int ma=-inf;u=1;
while(u!=0)
{
if(dp[u]>ma)
ma=dp[u];
u=cl[u];
}
printf("%d",ma);
return 0;
}标签:int inline image lin 图片 tor 决定 表示 代码
原文地址:https://www.cnblogs.com/lnzwz/p/11637986.html