标签:ever lock 了解 梯度 lse 变化 from height mda
凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
mean shift, 写的更符合国人的习惯,应该是mean of shift,也就是平均偏移量,或者偏移均值向量。在明确了含义之后,就可以开始如下的具体讲解了。
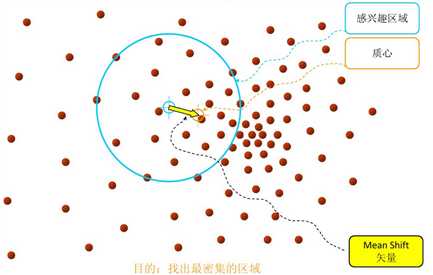
1). 基本形式
其中 为
个样本点,
,
为以
为中心的半径为
的高维球体,表示有效区域,其中包含
个样本点。其变形如下:
由此可以可知, 作为x的偏移均值向量,可用来对
进行更新,但这种更新有什么意义呢?通过简单的二维样本模拟,可以发现其倾向于向有效区域中样本密度高(即概率密度大)的地方移动。
2). 改进形式
基本形式中隐含了在有效区域中对所有的样本点一视同仁的假设,但这通常是不成立,最常见的就是随着距离的增加,作用就越小,因此,就有了如下的改进形式:
其中 为核函数,
表示带宽(严格来讲因为带宽矩阵,为对角矩阵,但通常对角元素取相等,故可表示为标量),
为样本权重。
由此可对基本形式进行更为合理的表示,采用均匀核函数,从而达到统一表示:
1). 数学推导
概率密度估计中,常用的方法有直方图估计、K近邻估计、核函数估计,其中核函数估计的表示如下:
其中 同样表示核函数。对概率密度函数
求导如下:
令 ,其亦是核函数,进一步分解,有如下表示:
可以看出,其中第二项也是一种概率密度的核函数估计,将其表示为 ,第三项则为上文中的mean shift的改进形式,因此,可以改写为:
接下来是两种解释,首先,求解概率密度局部极大值,令 ,由于
,故有:
这表示mean shift的本质是在求解概率密度局部极大值,即偏移均值向量让目标点始终向概率密度极大点处移动。但当数据量非常大时,一次遍历所有样本点显然不合适,故常选取目标点 附近的一个区域,进行贪心迭代,逐步收敛于概率密度极大值处;另一种更合理的解释是,通过在核函数
中融合进一个均匀核函数来表示选取的有效区域,然后迭代直至收敛。
再者,从梯度上升的优化角度来讲,有如下表示:
即偏移均值向量的作用等价于以概率密度为目标的具有自适应步长的梯度上升优化,其在概率密度较小的位置步长较大,当逼近局部极大点时,概率密度较大,因此步长较小,符合梯度优化中步长变化的需要。
由此,便对mean shift的含义及其合理性进行了解释,也就不难理解为何mean shift具有强大的效果及适用性了。
2). 泛化拓展
进一步拓展,虽然一般形式的mean shift是由概率密度的核函数估计推导出来的,其核心是核函数,但由于其具有归一化表示的性质,因此,理论上可以泛化为如下表示形式:
其中 确定偏移向量
的整体权重,可以任意选取,但必然需要具有一定的意义。显然偏移均值向量会倾向于权重较大的样本点,因此,从概率密度最大化的角度来看,
可以是
处概率密度的一种表示。
testMeanShift.m
clear
clc
profile on
bandwidth = 1;
%% 加载数据
data_load=dlmread(‘gauss_data.txt‘);
[~,dim]=size(data_load);
data=data_load(:,1:dim-1);
x=data‘;
%% 聚类
tic
[clustCent,point2cluster,clustMembsCell] = MeanShiftCluster(x,bandwidth);
% clustCent:聚类中心 D*K, point2cluster:聚类结果 类标签, 1*N
toc
%% 作图
numClust = length(clustMembsCell);
figure(2),clf,hold on
cVec = ‘bgrcmykbgrcmykbgrcmykbgrcmyk‘;%, cVec = [cVec cVec];
for k = 1:min(numClust,length(cVec))
myMembers = clustMembsCell{k};
myClustCen = clustCent(:,k);
plot(x(1,myMembers),x(2,myMembers),[cVec(k) ‘.‘])
plot(myClustCen(1),myClustCen(2),‘o‘,‘MarkerEdgeColor‘,‘k‘,‘MarkerFaceColor‘,cVec(k), ‘MarkerSize‘,10)
end
title([‘no shifting, numClust:‘ int2str(numClust)])
MeanShiftCluster.m
function [clustCent,data2cluster,cluster2dataCell] = MeanShiftCluster(dataPts,bandWidth,plotFlag)
%perform MeanShift Clustering of data using a flat kernel
%
% ---INPUT---
% dataPts - input data, (numDim x numPts)
% bandWidth - is bandwidth parameter (scalar)
% plotFlag - display output if 2 or 3 D (logical)
% ---OUTPUT---
% clustCent - is locations of cluster centers (numDim x numClust)
% data2cluster - for every data point which cluster it belongs to (numPts)
% cluster2dataCell - for every cluster which points are in it (numClust)
%
% Bryan Feldman 02/24/06
% MeanShift first appears in
% K. Funkunaga and L.D. Hosteler, "The Estimation of the Gradient of a
% Density Function, with Applications in Pattern Recognition"
%*** Check input ****
if nargin < 2
error(‘no bandwidth specified‘)
end
if nargin < 3
plotFlag = true;
plotFlag = false;
end
%**** Initialize stuff ***
[numDim,numPts] = size(dataPts);
numClust = 0;
bandSq = bandWidth^2;
initPtInds = 1:numPts;
maxPos = max(dataPts,[],2); %biggest size in each dimension
minPos = min(dataPts,[],2); %smallest size in each dimension
boundBox = maxPos-minPos; %bounding box size
sizeSpace = norm(boundBox); %indicator of size of data space
stopThresh = 1e-3*bandWidth; %when mean has converged
clustCent = []; %center of clust
beenVisitedFlag = zeros(1,numPts); %track if a points been seen already
numInitPts = numPts; %number of points to posibaly use as initilization points
clusterVotes = zeros(1,numPts); %used to resolve conflicts on cluster membership
while numInitPts
tempInd = ceil( (numInitPts-1e-6)*rand); %pick a random seed point
stInd = initPtInds(tempInd); %use this point as start of mean
myMean = dataPts(:,stInd); % intilize mean to this points location
myMembers = []; % points that will get added to this cluster
thisClusterVotes = zeros(1,numPts); %used to resolve conflicts on cluster membership
while 1 %loop untill convergence
sqDistToAll = sum((repmat(myMean,1,numPts) - dataPts).^2); %dist squared from mean to all points still active
inInds = find(sqDistToAll < bandSq); %points within bandWidth
thisClusterVotes(inInds) = thisClusterVotes(inInds)+1; %add a vote for all the in points belonging to this cluster
myOldMean = myMean; %save the old mean
myMean = mean(dataPts(:,inInds),2); %compute the new mean
myMembers = [myMembers inInds]; %add any point within bandWidth to the cluster
beenVisitedFlag(myMembers) = 1; %mark that these points have been visited
%*** plot stuff ****
if plotFlag
figure(1),clf,hold on
if numDim == 2
plot(dataPts(1,:),dataPts(2,:),‘.‘)
plot(dataPts(1,myMembers),dataPts(2,myMembers),‘ys‘)
plot(myMean(1),myMean(2),‘go‘)
plot(myOldMean(1),myOldMean(2),‘rd‘)
pause
end
end
%**** if mean doesn‘t move much stop this cluster ***
if norm(myMean-myOldMean) < stopThresh
%check for merge posibilities
mergeWith = 0;
for cN = 1:numClust
distToOther = norm(myMean-clustCent(:,cN)); %distance from posible new clust max to old clust max
if distToOther < bandWidth/2 %if its within bandwidth/2 merge new and old
mergeWith = cN;
break;
end
end
if mergeWith > 0 % something to merge
clustCent(:,mergeWith) = 0.5*(myMean+clustCent(:,mergeWith)); %record the max as the mean of the two merged (I know biased twoards new ones)
%clustMembsCell{mergeWith} = unique([clustMembsCell{mergeWith} myMembers]); %record which points inside
clusterVotes(mergeWith,:) = clusterVotes(mergeWith,:) + thisClusterVotes; %add these votes to the merged cluster
else %its a new cluster
numClust = numClust+1; %increment clusters
clustCent(:,numClust) = myMean; %record the mean
%clustMembsCell{numClust} = myMembers; %store my members
clusterVotes(numClust,:) = thisClusterVotes;
end
break;
end
end
initPtInds = find(beenVisitedFlag == 0); %we can initialize with any of the points not yet visited
numInitPts = length(initPtInds); %number of active points in set
end
[val,data2cluster] = max(clusterVotes,[],1); %a point belongs to the cluster with the most votes
%*** If they want the cluster2data cell find it for them
if nargout > 2
cluster2dataCell = cell(numClust,1);
for cN = 1:numClust
myMembers = find(data2cluster == cN);
cluster2dataCell{cN} = myMembers;
end
end
数据见:MATLAB中“fitgmdist”的用法及其GMM聚类算法,保存为gauss_data.txt文件,数据最后一列是类标签。
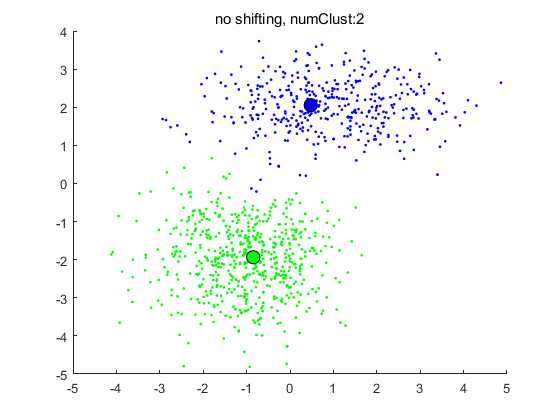
注意:聚类结果与核函数中的参数带宽bandwidth有很大关系,视具体数据而定。
标签:ever lock 了解 梯度 lse 变化 from height mda
原文地址:https://www.cnblogs.com/kailugaji/p/11646167.html