标签:onclick cas bre 乘法 n+2 转换 inf csdn 讲解
思想启发来自,
对于矩阵乘法和矩阵快速幂就不多重复了,网上很多博客都有讲解。主要来学习一下系数矩阵的构造
一开始,最一般的矩阵快速幂,要斐波那契数列Fn=Fn-1+Fn-2的第n项,想必都知道可以构造矩阵来转移
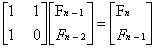
其中,前面那个矩阵就叫做系数矩阵(我比较喜欢叫转移矩阵)
POJ3070 Fibonacci 可以试一试

1 #include<cstdio> 2 typedef long long ll; 3 const ll md=10000; 4 struct Mar{ 5 int r,c; 6 ll a[10][10]; 7 Mar(){} 8 Mar(int r,int c):r(r),c(c){ 9 for(int i=0;i<r;i++) 10 for(int j=0;j<c;j++) a[i][j]=0; 11 } 12 }A,T; 13 Mar mul(Mar A,Mar B){ 14 Mar ans(A.r,B.c); 15 for(int i=0;i<A.r;i++) 16 for(int j=0;j<B.c;j++) 17 for(int k=0;k<A.c;k++){ 18 ans.a[i][j]+=A.a[i][k]*B.a[k][j]%md; 19 if(ans.a[i][j]>=md) ans.a[i][j]-=md; 20 } 21 return ans; 22 } 23 Mar poww(Mar A,int b){ 24 Mar ans(A.r,A.c); 25 for(int i=0;i<A.r;i++) ans.a[i][i]=1; 26 while(b){ 27 if(b&1) ans=mul(ans,A); 28 A=mul(A,A); 29 b>>=1; 30 } 31 return ans; 32 } 33 void init(ll a,ll b){ 34 A=Mar(2,1); 35 T=Mar(2,2); 36 A.a[0][0]=b;A.a[1][0]=a; 37 T.a[0][0]=T.a[0][1]=T.a[1][0]=1; 38 } 39 int main(){ 40 int t,n; 41 ll a,b; 42 while(~scanf("%d",&n)&&n!=-1){ 43 if(n==0) printf("0\n"); 44 else{ 45 init(1,0); 46 T=poww(T,n); 47 A=mul(T,A); 48 printf("%lld\n",A.a[0][0]); 49 } 50 } 51 return 0; 52 }
然后像类斐波那契数列Fn=a*Fn-1+b*Fn-2 ,也就变一下系数矩阵
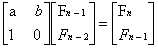
而如果是要求斐波那契的前n项和,除去我们知道的第n+2项-1,那对于类斐波那契的前n项和,我们可以设Sn=Sn-1+Fn,然后构造系数矩阵
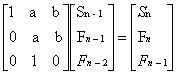
然后对于一些递推公式,转换一下前后几项的关系,也可以构造相应的系数矩阵来矩阵快速幂求解,比如求Σix的前n项和的话,设Fn=nx,Sn=Sn-1+Fn
那么nx可以写成(n-1+1)x的形式,把n-1设为a,1设为b,然后就是二项式定理展开了,(二项式展开看右边→_→)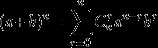
我们就可以得到一个n-1向n转移的递推过程,nx=Cxx(n-1)x+Cxx(n-1)x-1+...+C0x (n-1)0就可以构造系数矩阵
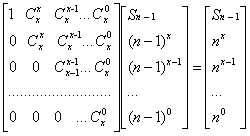
题意:F1=a,F2=b,Fn=Fn-1+2*Fn-2+n4,给出n求Fn
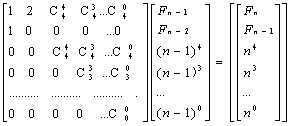

1 #include<cstdio> 2 typedef long long ll; 3 const ll md=2147493647; 4 struct Mar{ 5 int r,c; 6 ll a[10][10]; 7 Mar(){} 8 Mar(int r,int c):r(r),c(c){ 9 for(int i=0;i<r;i++) 10 for(int j=0;j<c;j++) a[i][j]=0; 11 } 12 }A,T; 13 Mar mul(Mar A,Mar B){ 14 Mar ans(A.r,B.c); 15 for(int i=0;i<A.r;i++) 16 for(int j=0;j<B.c;j++) 17 for(int k=0;k<A.c;k++){ 18 ans.a[i][j]+=A.a[i][k]*B.a[k][j]%md; 19 if(ans.a[i][j]>=md) ans.a[i][j]-=md; 20 } 21 return ans; 22 } 23 Mar poww(Mar A,int b){ 24 Mar ans(A.r,A.c); 25 for(int i=0;i<A.r;i++) ans.a[i][i]=1; 26 while(b){ 27 if(b&1) ans=mul(ans,A); 28 A=mul(A,A); 29 b>>=1; 30 } 31 return ans; 32 } 33 void init(ll a,ll b){ 34 A=Mar(7,1); 35 T=Mar(7,7); 36 A.a[0][0]=b;A.a[1][0]=a; 37 for(int i=6,j=1;i>=2;i--,j<<=1) A.a[i][0]=j; 38 T.a[0][0]=1;T.a[0][1]=2;T.a[1][0]=1; 39 for(int i=6;i>=2;i--){ 40 T.a[i][6]=1; 41 for(int j=5;j>=i;j--) 42 T.a[i][j]=T.a[i+1][j]+T.a[i+1][j+1]; 43 } 44 for(int i=2;i<7;i++) T.a[0][i]=T.a[2][i]; 45 } 46 int main(){ 47 int t,n; 48 ll a,b; 49 scanf("%d",&t); 50 while(t--){ 51 scanf("%d%lld%lld",&n,&a,&b); 52 if(n==1) printf("%lld\n",a%md); 53 else if(n==2) printf("%lld\n",b%md); 54 else{ 55 init(a,b); 56 T=poww(T,n-2); 57 A=mul(T,A); 58 printf("%lld\n",A.a[0][0]); 59 } 60 } 61 return 0; 62 }
那么(an+b)x的前n项和呢,还是把n写成n-1+1的形式,然后(a(n-1)+1+b)x二项式分解
(an+b)x=Cxx(n-1)x*ax*(a+b)0+Cxx(n-1)x-1*ax-1*(a+b)1+...+C0x (n-1)0*a0*(a+b)x,然后构造系数矩阵
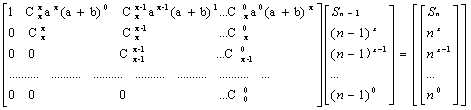
题意:有个机器人第n天学nk个单词,但星期六和星期天休息,不学单词,给出n,k,问机器一共学了多少个单词。
我们已经可以求nk的前n项和了,那么接下来只需要求出星期六和星期天的再减去,即可。
那么,我们根据开始的星期几到下一个星期六距离的天数x,和下一个星期天距离的天数x+1,
那么要减去的部分就是,(7m1+x)k 和(7m2+x+1)k的前m项和m1=(n-x)/7,m2=(n-x-1)/7,且第一项分别是xk和(x+1)k
(转移矩阵懒得画了)

1 #include<cstdio> 2 typedef long long ll; 3 const ll md=1e9+7; 4 struct Mar{ 5 int r,c; 6 ll a[25][25]; 7 Mar(){} 8 Mar(int r,int c):r(r),c(c){ 9 for(int i=0;i<r;i++) 10 for(int j=0;j<c;j++) a[i][j]=0; 11 } 12 }A,T; 13 char s[25]; 14 ll cf[25][25]; 15 Mar mul(Mar A,Mar B){ 16 Mar ans(A.r,B.c); 17 for(int i=0;i<A.r;i++) 18 for(int j=0;j<B.c;j++) 19 for(int k=0;k<A.c;k++){ 20 ans.a[i][j]+=A.a[i][k]*B.a[k][j]%md; 21 if(ans.a[i][j]>=md) ans.a[i][j]-=md; 22 } 23 return ans; 24 } 25 Mar poww(Mar A,int b){ 26 Mar ans(A.r,A.c); 27 for(int i=0;i<A.r;i++) ans.a[i][i]=1; 28 while(b){ 29 if(b&1) ans=mul(ans,A); 30 A=mul(A,A); 31 b>>=1; 32 } 33 return ans; 34 } 35 void init(int n,ll f0,ll a,ll b){ 36 A=Mar(n,1); 37 T=Mar(n,n); 38 A.a[0][0]=f0,A.a[n-1][0]=1; 39 for(int i=n-1;i>=1;i--){ 40 T.a[i][n-1]=1; 41 for(int j=n-2;j>=i;j--){ 42 T.a[i][j]=T.a[i+1][j]+T.a[i+1][j+1]; 43 if(T.a[i][j]>=md) T.a[i][j]-=md; 44 } 45 } 46 T.a[0][0]=1; 47 for(int i=1;i<n;i++){ 48 T.a[0][i]=T.a[1][i]; 49 T.a[0][i]*=cf[a][n-1-i]; 50 if(T.a[0][i]>=md) T.a[0][i]%=md; 51 T.a[0][i]*=cf[a+b][i-1]; 52 if(T.a[0][i]>=md) T.a[0][i]%=md; 53 } 54 } 55 ll solve(int n,int m,int x){ 56 ll ans1,ans2,ans3; 57 init(m+2,0,1,0);T=poww(T,n); 58 A=mul(T,A);ans1=A.a[0][0]; 59 init(m+2,cf[x][m],7,x);T=poww(T,(n-x)/7); 60 A=mul(T,A);ans2=A.a[0][0]; 61 init(m+2,cf[x+1][m],7,x+1);T=poww(T,(n-x-1)/7); 62 A=mul(T,A);ans3=A.a[0][0]; 63 return ((((ans1-ans2)%md+md)%md-ans3)%md+md)%md; 64 } 65 int main(){ 66 for(int i=0;i<=20;i++){ 67 cf[i][0]=1; 68 for(int j=1;j<=15;j++){ 69 cf[i][j]=cf[i][j-1]*i; 70 if(cf[i][j]>=md) cf[i][j]%=md; 71 } 72 } 73 int t=1,T,n,m,x; 74 scanf("%d",&T); 75 while(t<=T){ 76 scanf("%s",s); 77 scanf("%d%d",&n,&m); 78 if(s[0]==‘M‘) x=6; 79 else if(s[0]==‘T‘&&s[1]==‘u‘) x=5; 80 else if(s[0]==‘W‘) x=4; 81 else if(s[0]==‘T‘) x=3; 82 else if(s[0]==‘F‘) x=2; 83 else if(s[0]==‘S‘&&s[1]==‘a‘) x=1; 84 else x=0; 85 ll ans=solve(n,m,x); 86 printf("Case %d: %lld\n",t++,ans); 87 } 88 return 0; 89 }
最后,如果是要求nxxn的前n项和呢,一样把n写成n-1+1,然后(n-1+1)xxn二项式分解
nxxn=Cxx(n-1)x*xn-1+1+Cxx(n-1)x-1*xn-1+1+...+C0x (n-1)0*xn-1+1,转移矩阵就有了
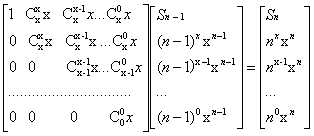
求nxxn的前n项和的模板题

1 #include<cstdio> 2 typedef long long ll; 3 const int N=111; 4 struct Mar{ 5 int r,c; 6 ll a[N][N]; 7 Mar(){} 8 Mar(int r,int c):r(r),c(c){ 9 for(int i=0;i<r;i++) 10 for(int j=0;j<c;j++) a[i][j]=0; 11 } 12 }A,T; 13 ll md ; 14 Mar mul(Mar A,Mar B){ 15 Mar ans(A.r,B.c); 16 for(int i=0;i<A.r;i++) 17 for(int j=0;j<B.c;j++) 18 for(int k=0;k<A.c;k++){ 19 ans.a[i][j]+=A.a[i][k]*B.a[k][j]%md; 20 if(ans.a[i][j]>=md) ans.a[i][j]-=md; 21 } 22 return ans; 23 } 24 Mar poww(Mar A,int b){ 25 Mar ans(A.r,A.c); 26 for(int i=0;i<A.r;i++) ans.a[i][i]=1; 27 while(b){ 28 if(b&1) ans=mul(ans,A); 29 A=mul(A,A); 30 b>>=1; 31 } 32 return ans; 33 } 34 void init(int n,int x){ 35 A=Mar(n,1); 36 T=Mar(n,n); 37 A.a[n-1][0]=1; 38 T.a[0][0]=1; 39 for(int i=n-1;i>=1;i--){ 40 T.a[i][n-1]=1; 41 for(int j=n-2;j>=i;j--){ 42 T.a[i][j]=T.a[i+1][j]+T.a[i+1][j+1]; 43 if(T.a[i][j]>=md) T.a[i][j]-=md; 44 } 45 } 46 for(int i=n-1;i>=1;i--) 47 for(int j=n-1;j>=i;j--){ 48 T.a[i][j]*=x; 49 if(T.a[i][j]>=md) T.a[i][j]%=md; 50 } 51 for(int i=1;i<n;i++) T.a[0][i]=T.a[1][i]; 52 } 53 int main(){ 54 int n,x; 55 while(~scanf("%d%d%lld",&n,&x,&md)){ 56 if(n<0&&x<0&&md<0) break; 57 init(x+2,x); 58 T=poww(T,n); 59 A=mul(T,A); 60 printf("%lld\n",A.a[0][0]); 61 } 62 return 0; 63 }
一些特殊的矩阵快速幂 hdu5950 hdu3369 hdu 3483
标签:onclick cas bre 乘法 n+2 转换 inf csdn 讲解
原文地址:https://www.cnblogs.com/LMCC1108/p/11655566.html