标签:font png details 后序 输出 过程 str src 传送门
我们平常使用的表达式一般为中缀表达式,而且一般只有中缀表达式有括号
将中缀表达式转化为表达式树方法:表达式树的树叶是操作数,而其他的节点为操作符,根节点为优先级最低且靠右的操作符,圆括号不包括。
如中缀表达式\(1 + (( 2 + 3)* 4 ) – 5\)转换后的表达式树如下:
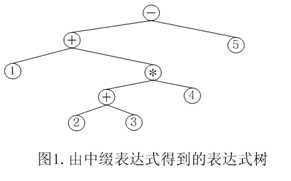
每次找优先级最低的最右边的运算符作为根,两边递归,直接建树,前缀表达式和后缀表达式分别为前序遍历和后序遍历
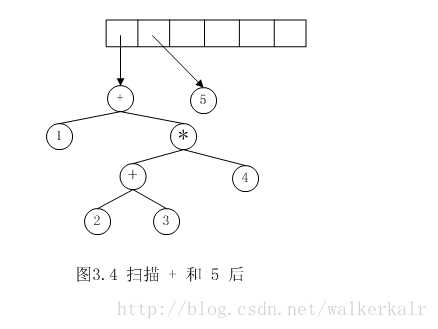
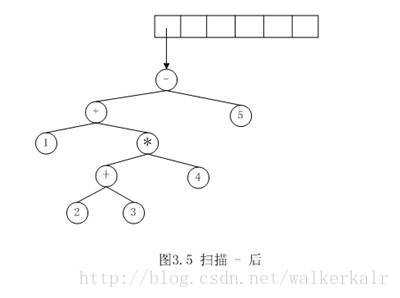
每读入一个字符压进栈中,若读入的是操作符则先将栈顶元素作为当前操作符的右子树,出栈,再将栈顶元素作为当前操作符的左子树,出栈,然后把这颗新的树的父亲节点入栈。
如后缀表达式$1 2 3 + 4 * +5 – $的转换
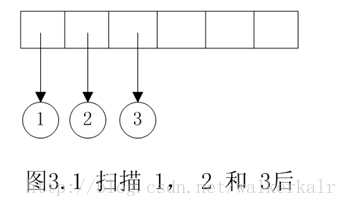
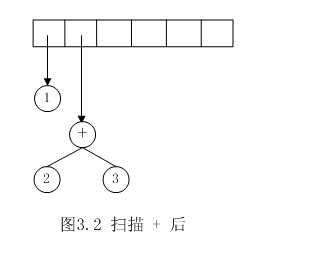
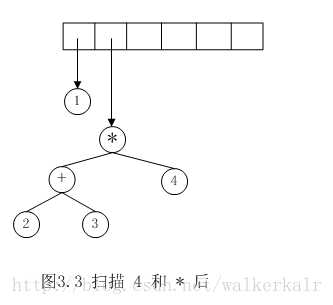
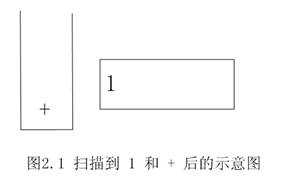
从左到右遍历中缀表达式的每个操作数和操作符。当读到操作数时,立即把它输出,即成为后缀表达式的一部分。
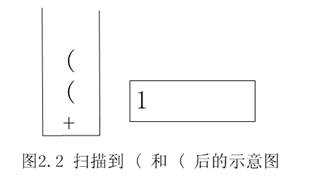
若读到操作符,判断该符号与栈顶符号的优先级,若该符号优先级高于栈顶元素,则将该操作符入栈,否则就一次把栈中运算符弹出并加到后缀表达式尾端,直到遇到优先级低于该操作符的栈元素,然后把该操作符压入栈中。(也就是维护了一个越靠近栈顶优先级越高的单调栈)如果遇到\(”(”\),直接压入栈中,如果遇到一个\(”)”\),那么就将栈元素弹出并加到后缀表达式尾端(弹一个加一个),但左右括号并不输出。
最后,如果读到中缀表达式的尾端,将栈元素依次完全弹出并加到后缀表达式尾端。(别忘了)
例子:\(1 + (( 2 + 3)* 4 ) – 5\)




和上面过程相同,维护一个优先级向栈顶递增的单调栈,唯一不同的两点是
\(1.\)从右向左扫描中缀表达式
\(2.\)遇到")"加入栈中,遇到"("弹出
部分内容参考这篇博客传送门
标签:font png details 后序 输出 过程 str src 传送门
原文地址:https://www.cnblogs.com/Liuz8848/p/11691864.html