数据结构之二叉树

标签：int   http   amp   ring   后续遍历   string   alt   main   二叉树   

阅读目录

一、二叉树定义

二、二叉树遍历

二叉树定义

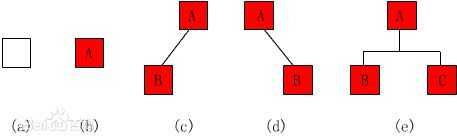
二叉树是递归定义的，其结点有左右子树之分，逻辑上二叉树有五种基本形态：
(1)空二叉树——如图(a)；
(2)只有一个根结点的二叉树——如图(b)；
(3)只有左子树——如图(c)；
(4)只有右子树——如图(d)；
(5)完全二叉树——如图(e)。

注意：尽管二叉树与树有许多相似之处，但二叉树不是树的特殊情形。 [1]
类型
(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。
(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

二叉树遍历

1. Golang实现

func main() {
    consBinaryTree()
}

type Hero struct {
    id    int
    name  string
    Left  *Hero
    Right *Hero
}

func consBinaryTree() {
    //构建二叉树
    root := &Hero{
        id:   1,
        name: "宋江",
    }
    left1 := &Hero{
        id:   2,
        name: "吴用",
    }
    left2 := &Hero{
        id:   4,
        name: "吴用1",
    }
    left3 := &Hero{
        id:   5,
        name: "吴用2",
    }
    right1 := &Hero{
        id:   3,
        name: "卢俊义",
    }
    root.Left = left1
    root.Right = right1

    right2 := &Hero{
        id:   4,
        name: "林冲",
    }
    right1.Right = right2
    left1.Left = left2
    left1.Right = left3
    //前序遍历
    PreOrder(root)
    //中序遍历
    InfixOrder(root)
}

//前序遍历 先输出root节点，然后在输出左子树，然后再输出右子树
func PreOrder(node *Hero) { //传入root  头节点
    if node != nil {
        fmt.Printf("name=%s, id=%d\n", node.name, node.id)
        PreOrder(node.Left)
        PreOrder(node.Right)
    }
}

//中序遍历，先输入root左子数，在输出root，在输出root右子树
func InfixOrder(node *Hero) { //传入root  头节点
    if node != nil {
        InfixOrder(node.Left)
        fmt.Printf("name=%s, id=%d\n", node.name, node.id)
        InfixOrder(node.Right)
    }
}

//后续遍历，先输入root左子数，在输出root右子树,在输出root
func PostOrder(node *Hero) { //传入root  头节点
    if node != nil {
        InfixOrder(node.Left)
        InfixOrder(node.Right)
        fmt.Printf("name=%s, id=%d\n", node.name, node.id)
    }
}

数据结构之二叉树

标签：int   http   amp   ring   后续遍历   string   alt   main   二叉树   

原文地址：https://www.cnblogs.com/zhangliang91/p/11700825.html