标签:com border 关系 一点 需要 影响 复杂 案例 条件
(续上小节)
前面的“改进型固定偏置”电路,虽然情况比原始的固定偏置电路好了一点,但还是不太理想,于是人们又设计出了性能更加稳定的分压偏置(voltage-divider bias configuration)电路,如下图所示:
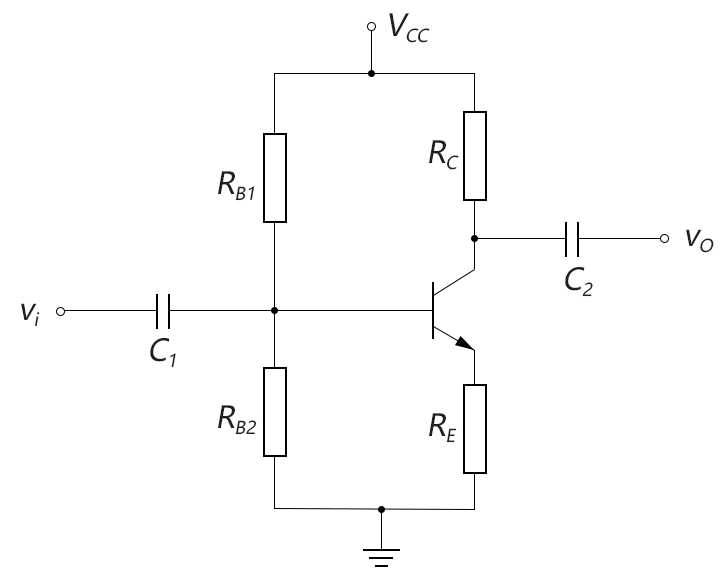
图3-6.06
分压偏置电路的稳定性非常完美,放大系数β的变化对输出静态工作点IC和VCE几乎没有什么影响,我们在下面的分析中可以验证这一点。
对于分压偏置的输入端分析,有“近似分析”和“精确分析”两种方法,一般在实际工程应用中,“近似分析”法基本就够用了,但是“精确分析”法你也是需要掌握的。对于学习来说,仔细揣摩和比较这两种方法,可以增强你对模拟电路关于什么时候可以作简化的直觉。
● 输入静态工作点:
我们将分压偏置的共射放大电路重画于下,在直流分析(静态分析)时,可将动态输入电压vi视为0。
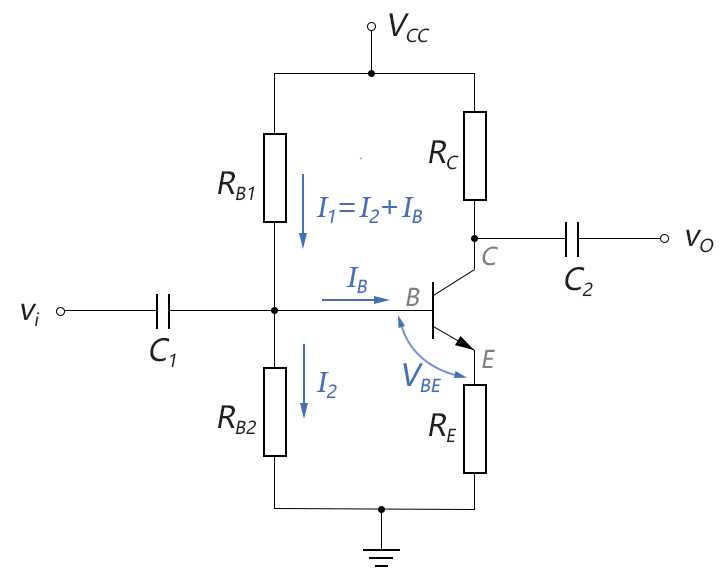
图3-6.07
上图中,由于IB为微安级,而I1和I2都为毫安级,因此,可以近似认为:I1≈I2。
作了如上近似后,基极B点的电压VB就很好算了,就是RB1和RB2对VCC的分压:
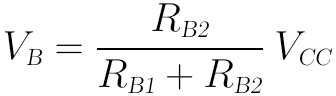
而E点电压VE即为:
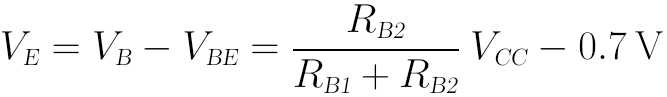
至于IB,由于我们刚才已经将IB近似为0了,故这里IB就无法再计算了。好在近似分析法中,即使我们不计算IB,也不影响后面的“输出静态工作点”的计算。
● 输出静态工作点:
由于在近似分析法中,IB已经近似为0,就不能用IC=β IB这个公式来计算IC了。我们需要用别的方法来计算IC,看下图:
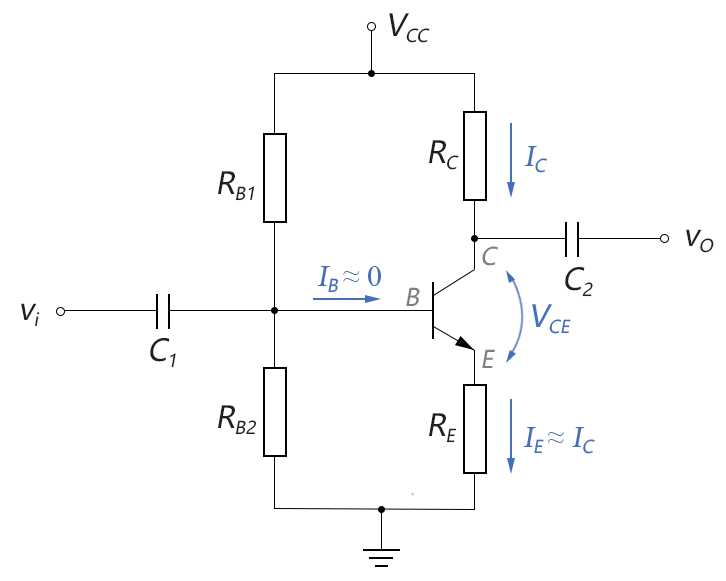
图3-6.08
在刚才的输入分析中,我们已经算得VE:
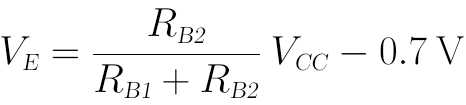
而IE即为:
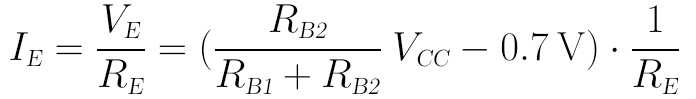
我们再近似认为:IC≈IE,即可得到:
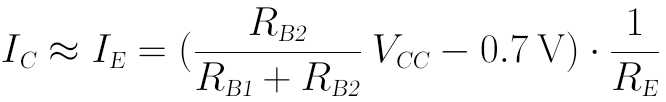
然后VCE即为:
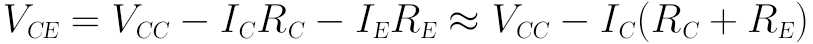
在精确分析法中,不再将IB近似为0,而是列出详尽的回路方程,然后进行数值解,如下图所示:(VBE仍简化为0.7V)
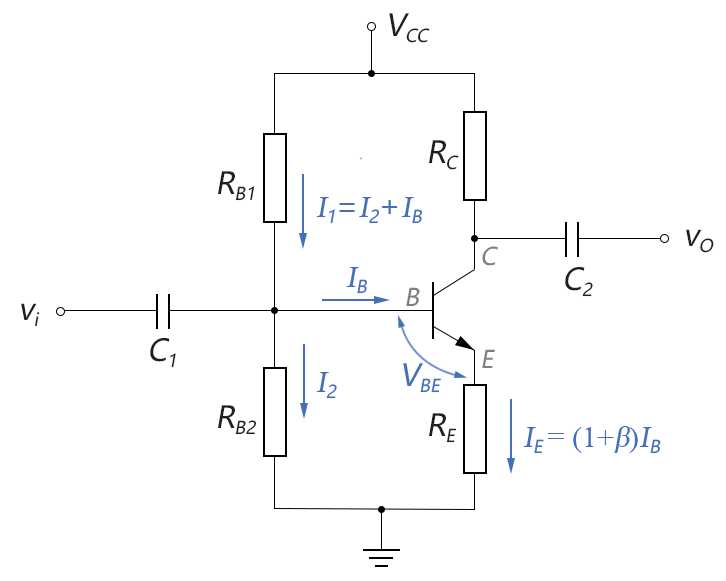
图3-6.09
对于上面的电路图,我们可以列出若干方程硬算,也可以借助一些电路等效化简方法巧妙地减少手算工作量,两者结果是一样的。下面分别予以介绍:
● 硬核计算:
对于上图,主要的电流关系式和主要的电压关系式为:
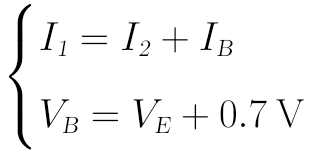
我们可以分别列出I1、I2、VE的欧姆定律计算式:
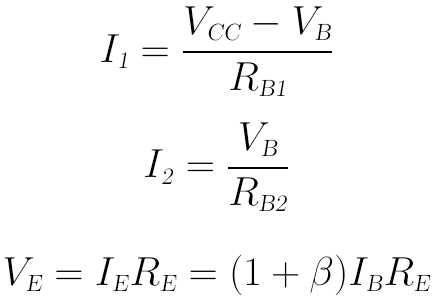
将它们代入上面的主电流、电压关系式可得:
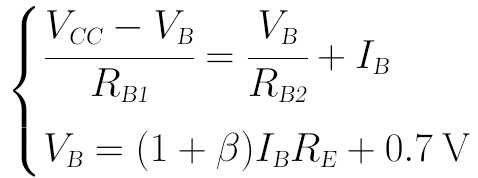
在上面这个方程组中,仅含有VB和IB两个未知变量。耐心一点、按部就班地一步步推算,是可以解出IB和VB的,IB最终可解得为:
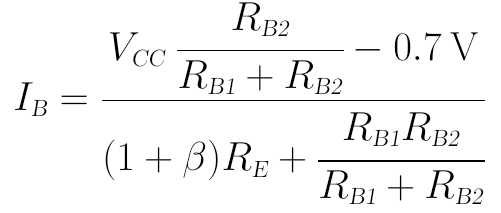
解出IB后,用IC=β IB的关系式,可以很方便地求出输出端的静态工作点IC和VCE,这里就不再重复写了。
● 电路等效化简后计算:
上面的方程组,看上去好像不算太复杂,但其实真的算起来,还是有一点工作量的(至少我用了三大张纸)。而且在解方程时把各个量颠来倒去地抄写,很容易出错。所以,一般在做电路计算时,会先考虑一下电路能不能化简,把电路尽量化简成等效的最简单形式,这样最终列出的方程就会比较简单,解起来也不太会出错。
电路等效化简最常用的方法就是:戴维南等效电路和诺顿等效电路,我们现在尝试用戴维南等效电路的方法,对上面的图3-6.09进行等效化简:
对于输入端的分析,从三极管的基极(B点)向左看,可以将B点左侧的外部电路视为一个戴维南等效电路,如下图所示:
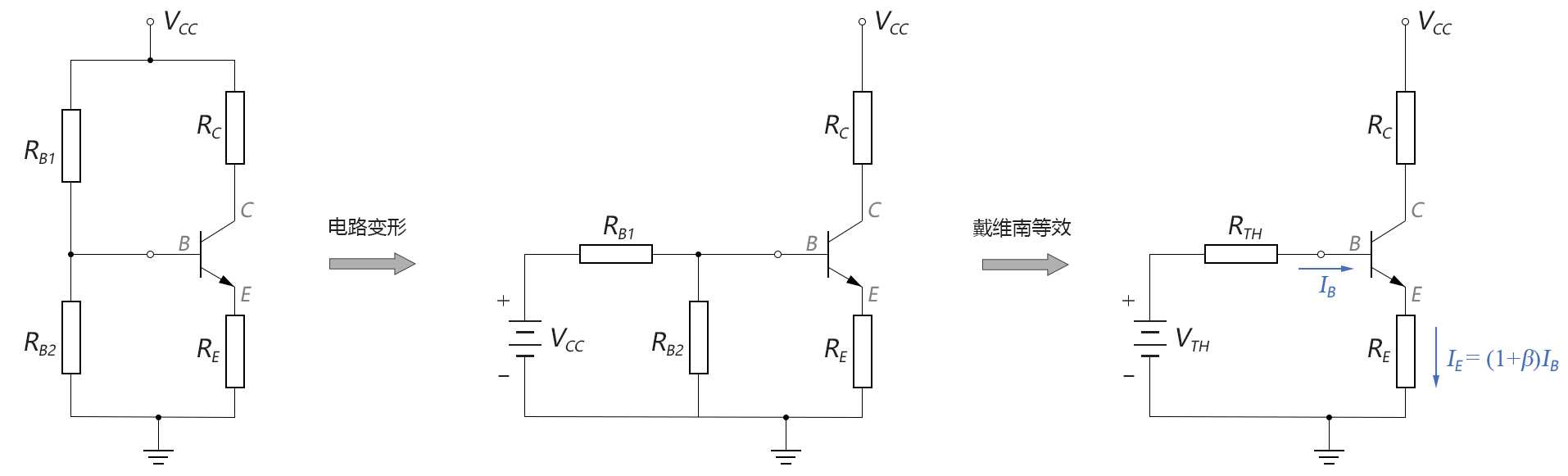
图3-6.10
对于上面做完戴维南等效的最右图,列写输入侧的KVL方程就很容易了:
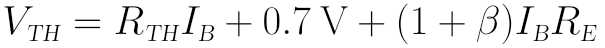
解得IB为:
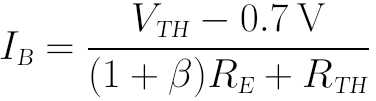
是不是要比上面的硬核计算法要简单很多?至于戴维南等效电压VTH和戴维南等效电阻RTH就很好算啦,如下图所示:
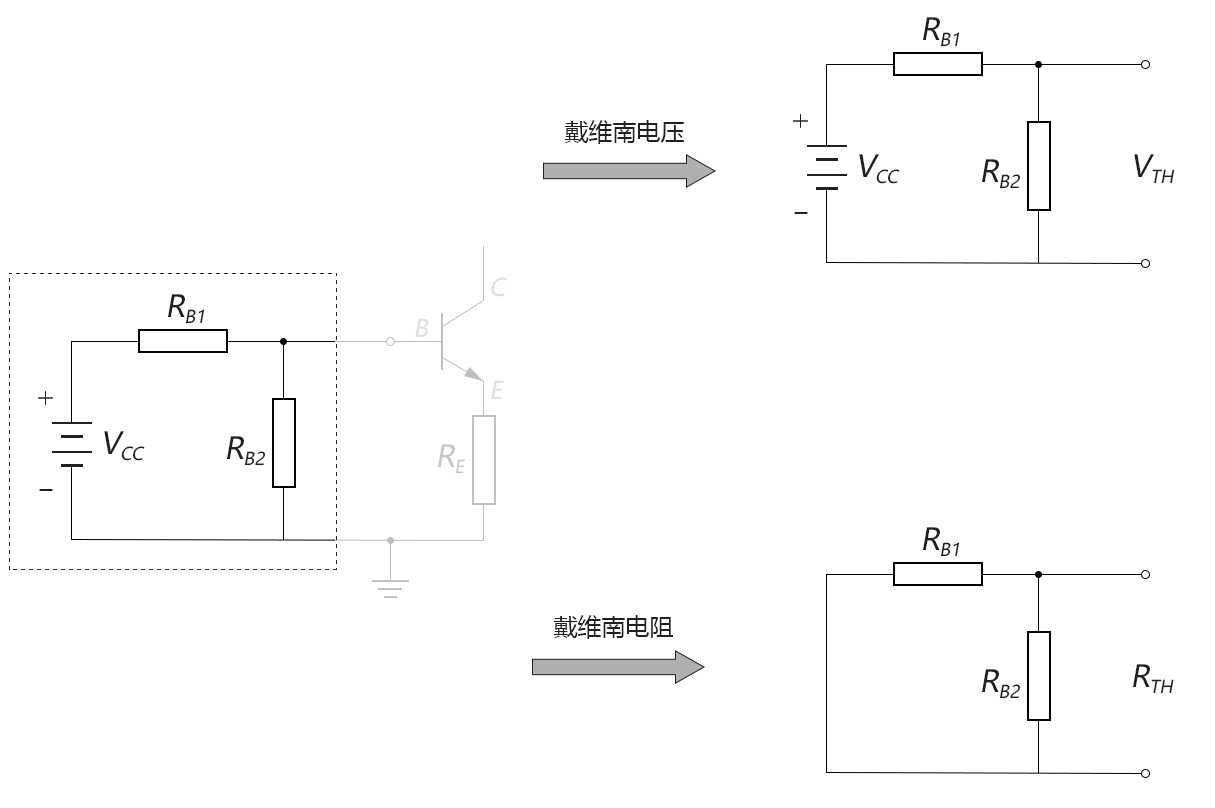
图3-6.11
计算戴维南等效电压VTH时,可将右侧视为开路:
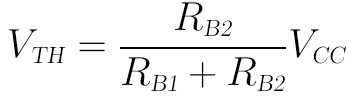
计算戴维南等效电阻RTH时,可将电压源VCC视为短路:
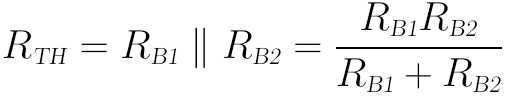
然后再将VTH和RTH代入上面的IB,最终结果和前面硬算的结果是一致的。
案例3-6-2:分别用近似分析法和精确分析法,计算下图分压偏置电路的IB, IC, VCE。
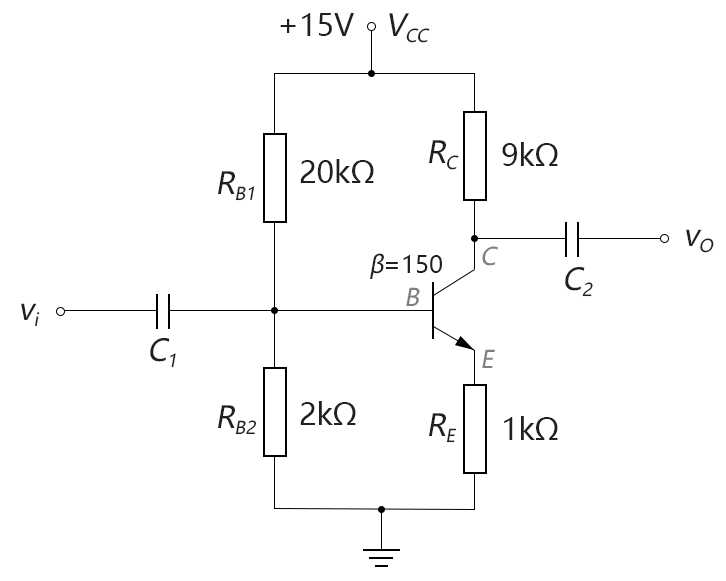
图3-6.a2
解:(1)近似分析法:
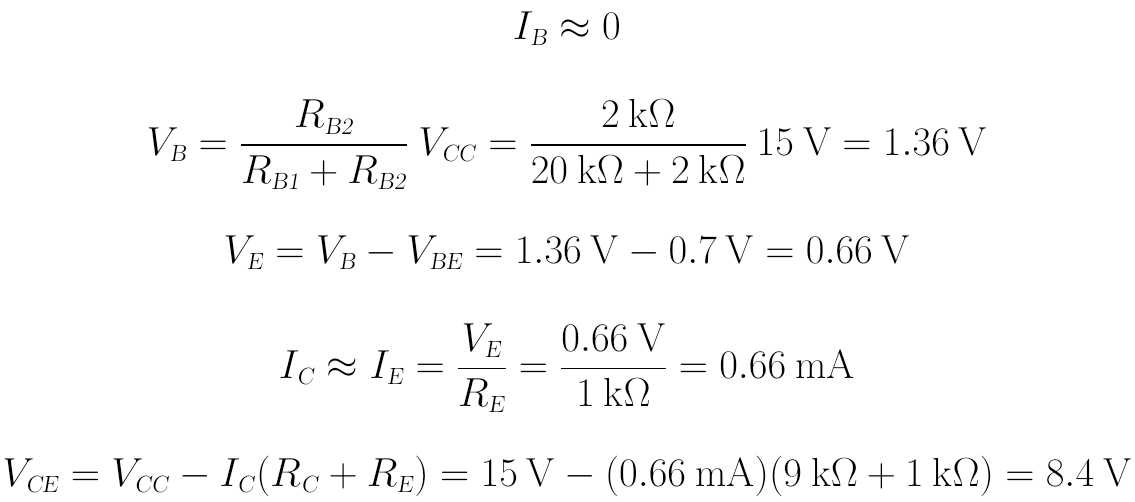
验证:VCE > VCEsat,说明BJT工作于放大区的假设正确。
(2)精确分析法:
先计算戴维南等效电压和电阻:
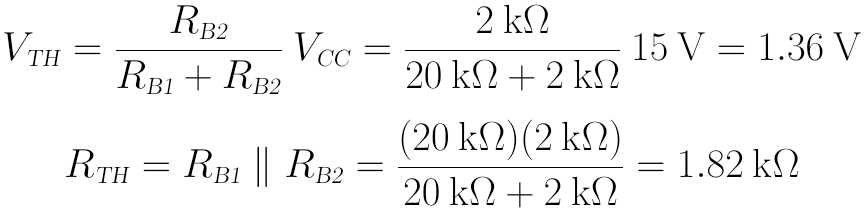
再将其代入IB计算式:
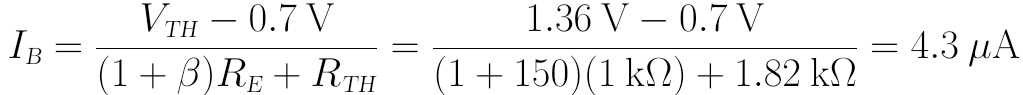
假设BJT工作于放大区:
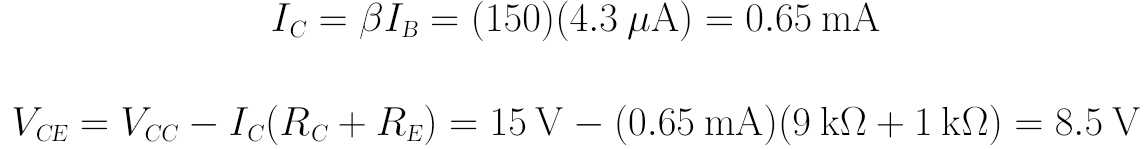
验证:VCE > VCEsat,说明BJT工作于放大区的假设正确。
比较:从上面两种方法计算得到的IC和VCE来看,两种算法的结果非常接近,故知近似分析法在大部分情况下是可以对电路进行大致评估计算的,而且近似分析法不需要用到β参数,说明分压偏置电路的静态工作点基本不受β影响。
当VCE<VCEsat时,晶体管进入饱和区。因此,我们可以算出此时的集电极饱和电流ICsat,
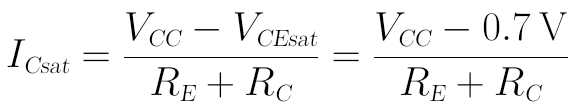
当IC>ICsat时,晶体管进入饱和。
( end of 3-6-2)
初级模拟电路:3-6 共射放大电路-2(分压偏置的直流分析)
标签:com border 关系 一点 需要 影响 复杂 案例 条件
原文地址:https://www.cnblogs.com/initcircuit/p/11703235.html