标签:hash冲突 get 自变量 tab 质数 好的 return info image
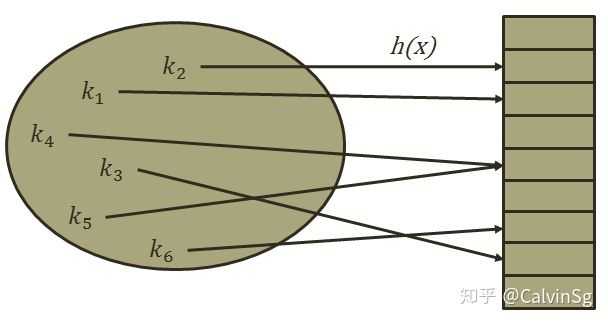
哈希表(Hash Table)是一种根据关键字(Key value)直接访问内存存储位置的数据结构。
通过哈希表,数据元素的存放位置和数据元素的关键字之间建立起某种映射对应关系,这个映射函数叫做散列函数,存放数据的数组叫做散列表。
假设要存储的数据元素个数为n,设置一个长度为m(m≥n)的连续存储单元,分别以每个数据元素的关键字 Ki(0<= i <=n-1) 为自变量,通过哈希函数 hash(Ki) 把 Ki 映射为内存单元的某个地址 hash(ki),并将该数据元素存储在该内存单元中。从数学的角度来看,哈希函数实际上是关键字到内存单元的映射,因此我们希望用哈希函数通过尽量简单的运算,使得通过哈希函数计算出的哈希地址尽量均匀地被映射到一系列的内存单元中。
第一,运算过程要尽量简单高效,以提高哈希表的插入和检索效率;
第二,哈希函数应该具有较好的散列性,以降低哈希冲突的概率;
第三,哈希函数应具有较大的压缩性,以节省内存。
1)直接定址法
该方法是取关键字的某个线性函数值为哈希地址。可以简单的表示为:
hash(K)=aK + C
优点是不会产生冲突,但缺点是空间复杂度可能会很高,适用于元素较少的情况下;
2)平方取中法
如果关键字的每一位都有某些数字重复出现频率很高的现象,可以先求关键字的平方值,通过平方扩大差异,而后取中间数位作为最终存储地址。
使用举例
比如key=1234 1234^2=1522756 取227作hash地址
比如key=4321 4321^2=18671041 取671作hash地址
这种方法适合事先不知道数据并且数据长度较小的情况
3)除留余数法
它是用数据元素关键字除以某个常数所得的余数作为哈希地址,该方法计算简单,适用范围广,是最经常使用的一种哈希函数,可以表示为:
hash(K)=K mod C (C<=m)m为表长
该方法的关键是常数的选取,一般要求是接近或等于哈希表本身的长度,理论研究表明,该常数取素数时效果最好。
在实际中,我们的键并不都是数字,有可能是字符串,还有可能是几个值的组合等,所以我们需要实现自己的哈希函数。
1. 正整数
获取正整数哈希值最常用的方法是使用除留余数法。即对于大小为素数M的数组,对于任意正整数k,计算k除以M的余数。M一般取素数。
2. 字符串
将字符串作为键的时候,我们也可以将他作为一个大的整数,采用保留除余法。我们可以将组成字符串的每一个字符取值然后进行哈希,比如
public int GetHashCode(string str)
{
char[] s = str.ToCharArray();
int hash = 0;
for (int i = 0; i < s.Length; i++)
{
hash = s[i] + (31 * hash);
}
return hash;
}
上面的哈希值是Horner计算字符串哈希值的方法,公式为:
h = s[0] · 31L–1 + … + s[L – 3] · 312 + s[L – 2] · 311 + s[L – 1] · 310
举个例子,比如要获取”call”的哈希值,字符串c对应的unicode为99,a对应的unicode为97,L对应的unicode为108,所以字符串”call”的哈希值为 3045982 = 99·313 + 97·312 + 108·311 + 108·310 = 108 + 31· (108 + 31 · (97 + 31 · (99)))
如果对每个字符去哈希值可能会比较耗时,所以可以通过间隔取N个字符来获取哈西值来节省时间,比如,可以 获取每8-9个字符来获取哈希值:
public int GetHashCode(string str)
{
char[] s = str.ToCharArray();
int hash = 0;
int skip = Math.Max(1, s.Length / 8);
for (int i = 0; i < s.Length; i+=skip)
{
hash = s[i] + (31 * hash);
}
return hash;
}
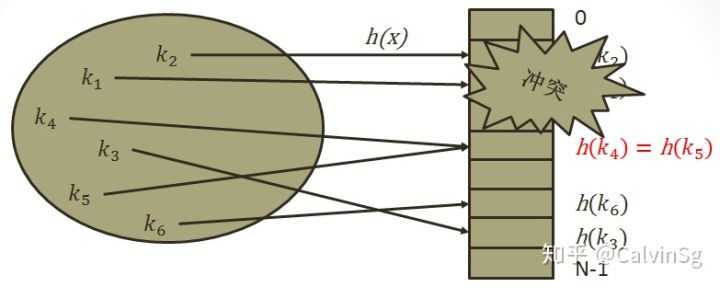
在构造哈希表时,存在这样的问题,对于两个不同的关键字,通过我们的哈希函数计算哈希地址时却得到了相同的哈希地址,我们将这种现象称为哈希冲突(如图):
比如我们使用除留余数法时,对于key:3、6、9, 3 mod 3 == 6 mod 3 == 9 mod 3 =0,此时3,6,9都发生了hash冲突。
1.开放定制法
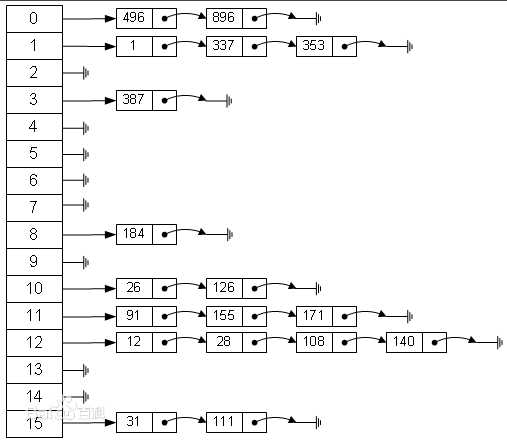
2.链地址法
首先有一个H(key)的哈希函数
如果H(key1)=H(keyi)
那么keyi存储位置
Hi?=(H(key)+di?)MODm(m为表长)
di?有三种取法
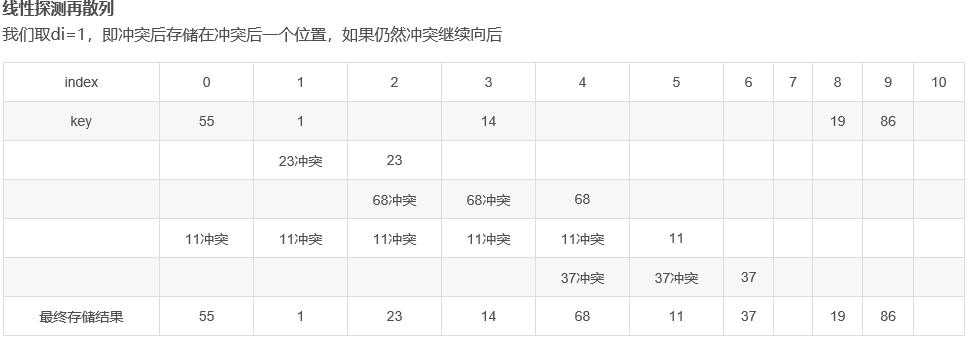
1)线性探测再散列
d i =c∗i
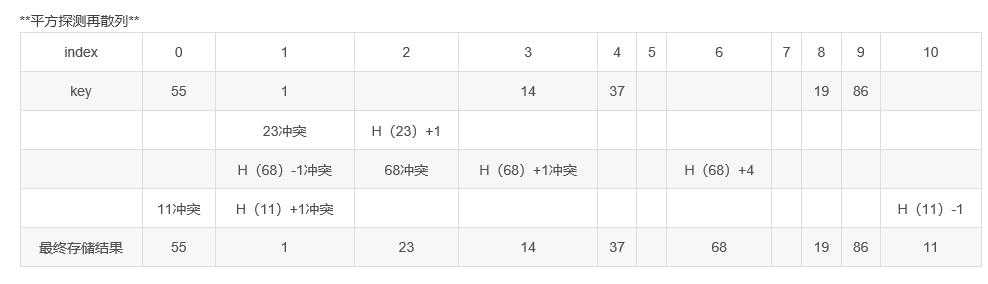
2)平方探测再散列
d_i=1^2,-1^2,2^2,-2^2
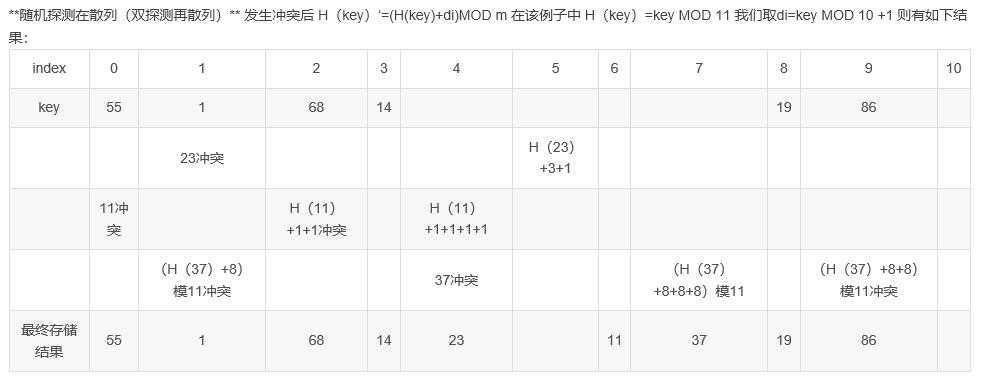
3)随机探测在散列(双探测再散列)
di?是一组伪随机数列
注意
增量di应该具有以下特点(完备性):产生的Hi(地址)均不相同,且所产生的s(m-1)个Hi能覆盖hash表中的所有地址
有一组数据
19 01 23 14 55 68 11 86 37要存储在表长11的数组中,其中H(key)=key MOD 11
那么按照上面三种解决冲突的方法,存储过程如下:
(表格解释:从前向后插入数据,如果插入位置已经占用,发生冲突,冲突的另起一行,计算地址,直到地址可用,后面冲突的继续向下另起一行。最终结果取最上面的数据(因为是最“占座”的数据))
链地址法的原理时如果遇到冲突,他就会在原地址新建一个空间,然后以链表结点的形式插入到该空间。
refer:
标签:hash冲突 get 自变量 tab 质数 好的 return info image
原文地址:https://www.cnblogs.com/-wenli/p/11703385.html