斐波那契数列的记忆搜索

标签：次数   输出   相同   数学   递归   title   enc   斐波那契   知识   

摘要

本blog通过”斐波那契数列求值“这个经典问题，分析并说明“从单一递归到记忆搜索”这个思想过程。本blog是整个动态规划学习的一部分。（记忆搜索是动态规划的递归写法）

斐波那契数列

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：(本身没有F(0)的，考虑到编程实际加上)
\[ F(0)=0,F(1)=1\F(2)=F(0)+F(1)=1\...\F(n)=F(n-1)+F(n-2) \]

经典递归分析

在代码中我加入了辅助输出

int F (int n)
{
    cout << "\nThis is F (" << n << ")";    //添加的辅助输出
    if (n == 0 || n == 1) return 1;         //递归边界
    else
    {
        cout << " = F (" << n-1 << ")+F (" << n-2 << ")" ;  //添加的辅助输出
        return F(n-1) + F(n-2);

    }
}

根据递归知识，绘制其算法过程的递归树：

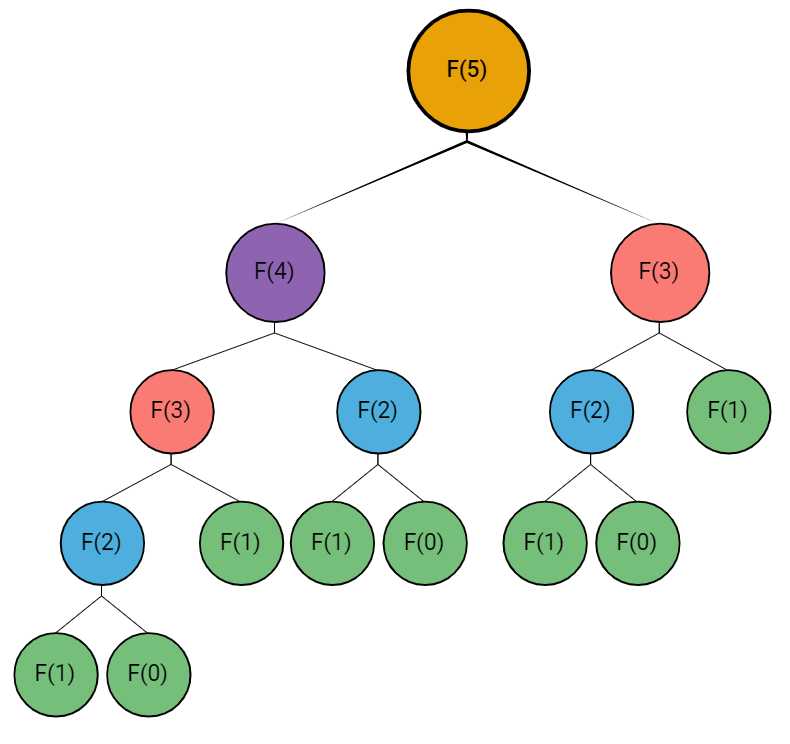
每个结点在该过程中都是需要计算的，不同颜色标记不同的中间结果，不难发现有部分的重复计算。如果数据规模n很大，重复计算的次数将难以想象，复杂度将高达\(O(2^n)\)。为了避免重复计算，不妨开辟一个维数组记录中间结果的值。这样，当下次再碰到相同的计算内容时，就能直接使用上一次的计算结果。（拿空间换时间的思路），这种记录过程中间结果的方式，称之为“记忆搜索”。复杂度降到\(O(n)\)，这正是动态规划采用的提高计算效率的方式。

动态规划分析

在代码中我加入了辅助输出

int dp[10];

int Fa (int n)
{
    cout << "\nThis Fa[" << n <<"]";    //添加的辅助输出
    if (n == 0 || n == 1)
        return 1;                       //递归边界
    if (dp[n] != -1)
    {
        cout << " find Fa[" << n <<"]"; //添加的辅助输出
        return dp[n];
    }
    else
    {
        cout << " calculate Fa[" << n-1 <<"] + Fa[" << n-2 <<"]";   //添加的辅助输出
        dp[n] = Fa(n-1) + Fa(n-2);
        return dp[n];
    }
}

同样绘制其算法过程的递归树：

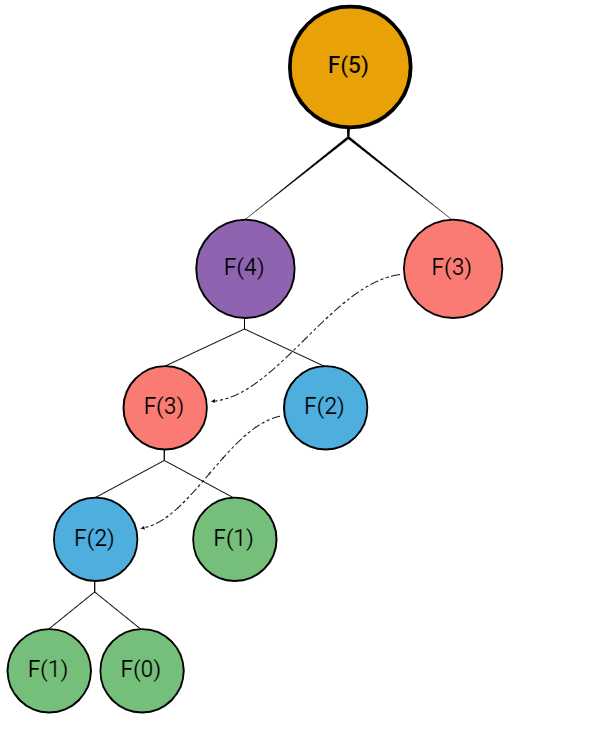
图中右侧的F(2)F(3)查询上一次的计算结果，节省下了单一递归的后序结点。

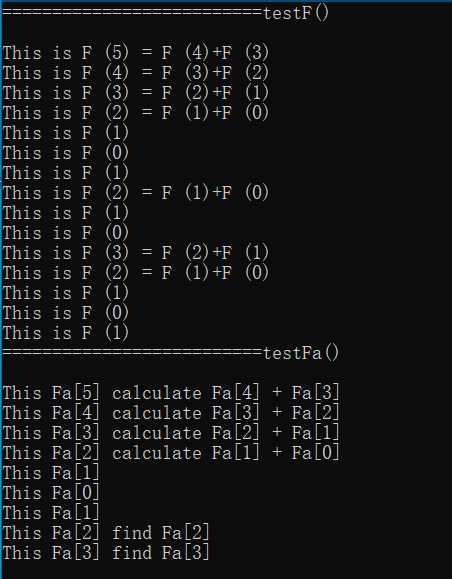
查看比较输出的结果，记忆搜索的第二次F(2)F(3)是利用查找确定值，而不是进一步的递归。

斐波那契数列的记忆搜索

标签：次数   输出   相同   数学   递归   title   enc   斐波那契   知识   

原文地址：https://www.cnblogs.com/goodswarm/p/11703482.html