标签:color 一条直线 更新 char and 第一步 数值 The 进入
裁剪作用:
选择显示的内容--图形在窗口内的部分被显示出来,窗口外的部分被裁剪掉
图形中每个图形基本元素都要经过裁剪,因此裁剪直接影响整个图形系统的效率。
裁剪窗口:矩形,凸多边形,任意多边形
裁剪类型:二维裁剪、三维裁剪
裁剪对象:直线段、多边形、文字等
裁剪方法:
直线的裁剪方法: Sutherland-Cohen算法 , Cyrus-Beck算法,梁友栋-Barsky算法
多边形的裁剪方法:Sutherland-Hodgman算法
三维的裁剪方法: Sutherland-Cohen算法 ,梁友栋-Barsky算法
本算法又称为编码裁剪算法
Sutherland–Cohen算法分成两部分:
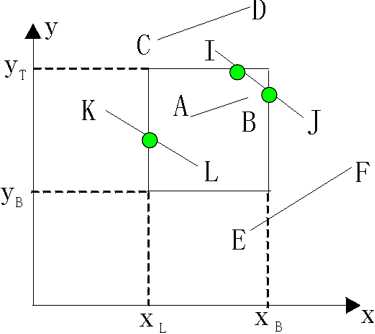
第一步,判定:
1) 完全在窗口内的直线段,称为完全可见的线段,如AB。保留着
2) 完全在窗口外的线段,称为完全不可见线段,如CD。抛弃掉
第二步,处理不能断定为完全可见或完全不可见的线段,如IJ、KL
*这时需要计算出直线段和窗口边界的一个交点,这个交点把直线分成两段,其中一条为完全不可见的线段,被抛弃。
*对余下部分再作第一步的判断,重复上述过程,直到直线段余下的部分可用第一步的判断得出肯定的结论为止。
为使计算机能够快速判断一条直线段与窗口属何种关系,采用如下编码方法。窗口的四条边把整个平面分成九个区域,每一个区域采用四位编码表示:
在x=xL左侧的区域,编码的第四位是1;
在x=xR右侧的区域,编码的第三位是1;
在y=yB下侧的区域,编码的第二位是1;
在y=yT上侧的区域,编码的第一位是1。
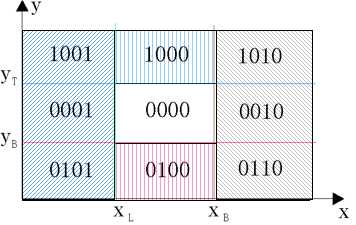
如何判断?
对要被裁剪的线段的两个端点进行区域编码。
如果其所在的区域的编码均是0000(相与),则这条线段完全可见;
如果两个编码的逻辑与不为0000,则这条线段完全不可见
线段KL为例,从K点(1001)的编码分析出K在x=xL的左侧,KL必和x=xL有交点,求出其交点M,KM显然是完全不可见的,因而只要对ML从第一步开始重复上述处理步骤。
由于ML还是不能用第一步下结论,又从M的编码发现M在y=yT的上侧,因而要求ML和y=yT的交点N。
丢掉MN,对NL用第一步的方法可断定NL为完全可见,至此裁剪结束。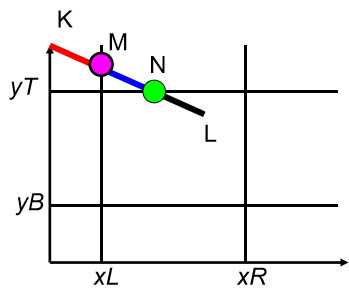
float xl, xr, yt, yb; unsigned char code(float x, float y) { unsigned char c = 0; if (x < xl) c = c|1; //按位或 else if (x > xr) c = c|2; if (y < yb) c = c|4; else if (y > yt) c = c|8; return c; }//给九个区域编码 void clip(float x0, float y0, float x2, float y2) { unsigned char c1, c2, c; float x, y, wx, wy; c1 = code(x0, y0); c2 = code(x2, y2); while ((!(c1 == 0)) || (!(c2 == 0))) { if ((c1& c2)) return; //两端点逻辑与不为0,则在区域外,裁去 c = c1; if (c == 0) c = c2; wx=x2-x0; wy=y2-y0; if ((c & 1) == 1) { y = y0 + wy * (xl - x0) /wx; x = xl; }//端点在xl左侧,求与xl的交点 else if ((c & 2) == 2) { y = y0 +wy * (xr - x0) /wx; x = xr; } //端点在xr右侧,求与xr的交点 else if ((c & 4) == 4) { x = x0 +wx * (yb - y0) /wy; y = yb; } //端点在yb下方,求与yb的交点 else if ((c & 8) == 8) { x = x0 +wx * (yt - y0) / wy; y = yt; } //端点在yt上方,求与yt的交点 if (c == c1) { x0 = x; y0 = y; c1 = code(x0, y0); } else { x2 = x; y2 = y; c2 = code(x2, y2); } //用交点代替端点,再返回第一步 }// While() glLine(int(x0), int(y0), int(x2), int(y2)); }
Cohen-Sutherland裁剪算法对不与边框相交的线段进行裁剪时效率较高,而对与窗口边界有交点的线段裁剪效率低。
因而比较适合两种情况的裁剪:一是大部分线段完全可见;二是大部分线段完全不可见。
而且很多的时候,被裁剪线段仅与窗口边界延长线相交,求交点到最后是无效的操作,因为线段可能完全被丢弃;并且被裁剪线段与窗口边界相交时交点的取得比较复杂。
比如像下图这样的裁剪,这条红色线段完全是在裁剪窗口的外部,却需要进行算法计算,最后线段完全被丢弃!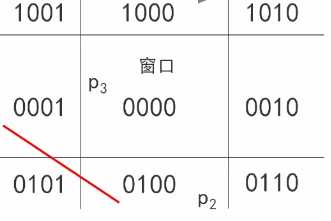
中点分隔算法是对Sutherland-Cohen算法在求交点方面的改进。
核心思想是通过二分逼近来确定直线段与 窗口的交点。
取线段的中点
1、若中点不在窗口内, 则把中点和离窗口边界最远点构成的线段丢掉,以线段上的另一点和该中点再构成线段求其中点
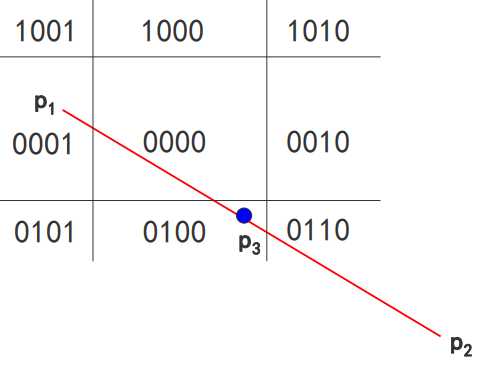
2、如中点在窗口内,则又以中点和最远点构成线段, 并求其中点,直到中点与窗口边界的 坐标值在规定的误差范围内相等
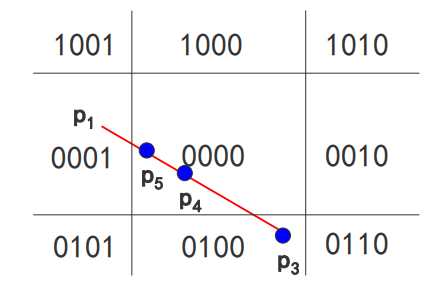
重复上述过程,直到线段长度小于给定的小数ε为止。
在显示时ε可取成一个象素的宽度,对分辨率为2N×2N的显示器来说,上面讲的二分的过程最多只要作N次。
Cyrus-Beck算法可以处理任意凸多边形对线段的裁剪。
考虑如图所示一个凸多边形区域R和一条线段P1P2,要求计算线段落在区域R中的部分。
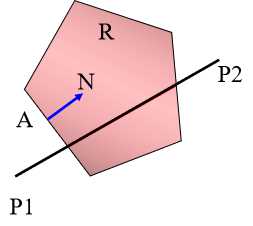
假定A是区域R边界L上一点;N是区域边界在A点的内法向量;线段P1P2用参数方程表示:
对于线段P1P2的参数方程表示,如果能判断出线段进入多边形时候的参数ts和线段退出多边形时的参数te,则tste之间的线段为裁剪完毕后的结果。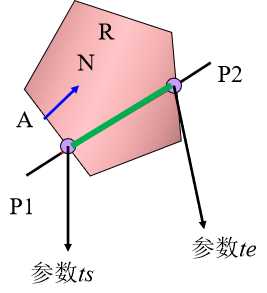
假定A为区域边界L上的任意一点,记L的内法向量(垂直)为N对于线段上任意一点 Pi, Pi和多边形边界L的关系有三种可能(t 为此点的参数值):
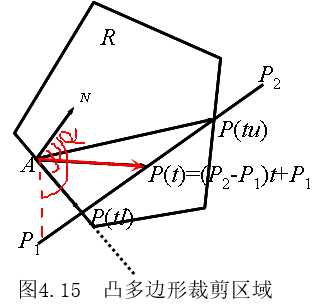


性质(1): 如果点P(t)在多边形所有边的内侧,则称P是在多边形的内侧。
可见线段的参数区间

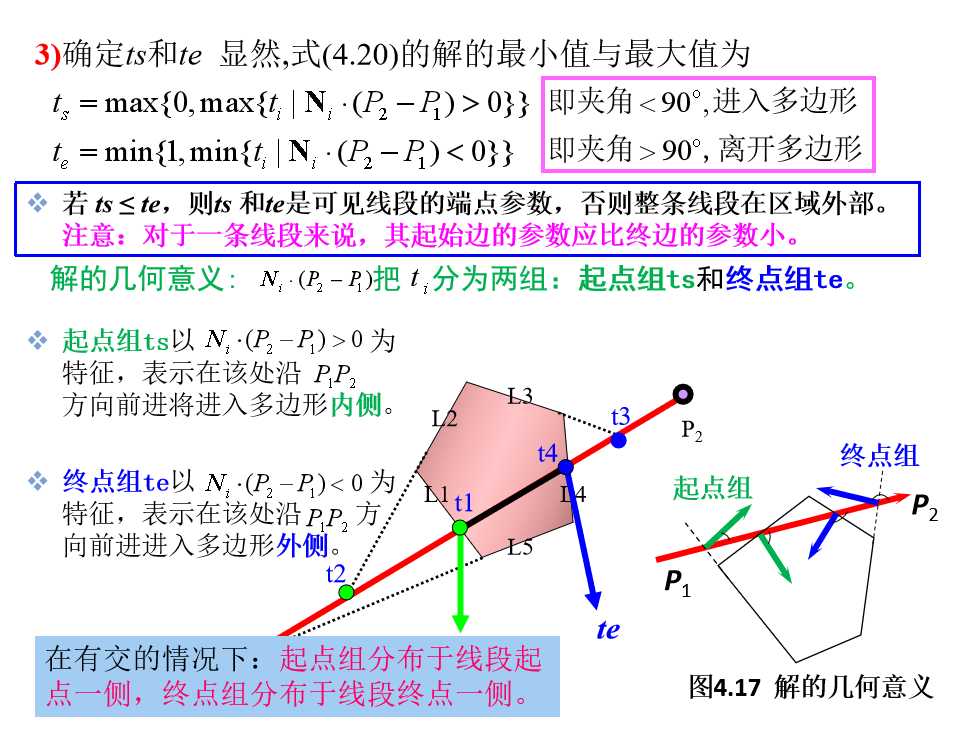

double ts,te; int Cyrus_Beck (int k,double A[][2],double N[][2],double x[2],double y[2],double *ts,double *te) { int i,j; double t,dn,nw,D[2],W[2]; *ts=0; *te=1; for(i=0; i<k; i++) { dn=N[i][0]*(x[1]- x[0])+N[i][1]* (y[1]-y[0]); nw=N[i][0]* (x[0]-A[i][0])+N[i][1]* (y[0]- A[i][1]); if(fabs(dn)<1.0e-6) //平行 { if(nw<0) return 0; //p在L外侧 } else { t=-nw/dn; if(dn<0) { if(t< *te) *te=t; //终点 } else if(t> *ts) *ts=t; //起点 } if(*ts>*te) return 0; //在区域外 } return 1; }
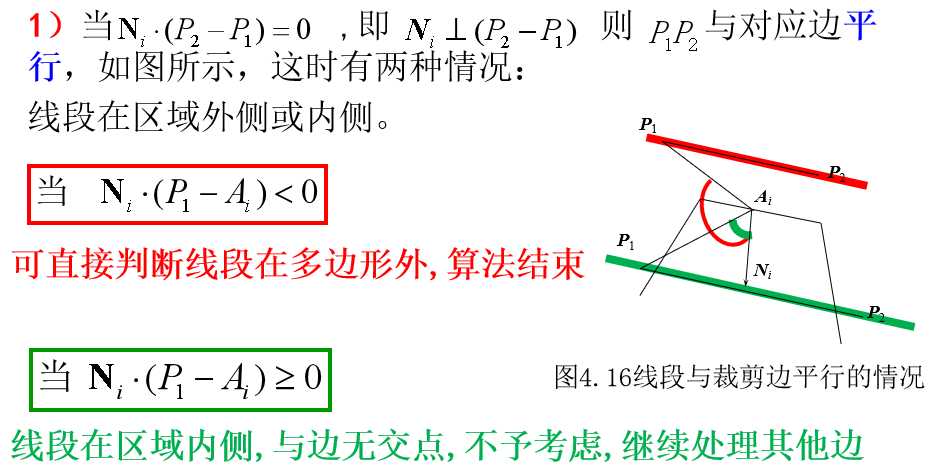
当凸多边形是矩形窗口,且矩形的边平行于坐标轴时, Cyrus-Beck算法可简化为梁友栋-Barsky算法。
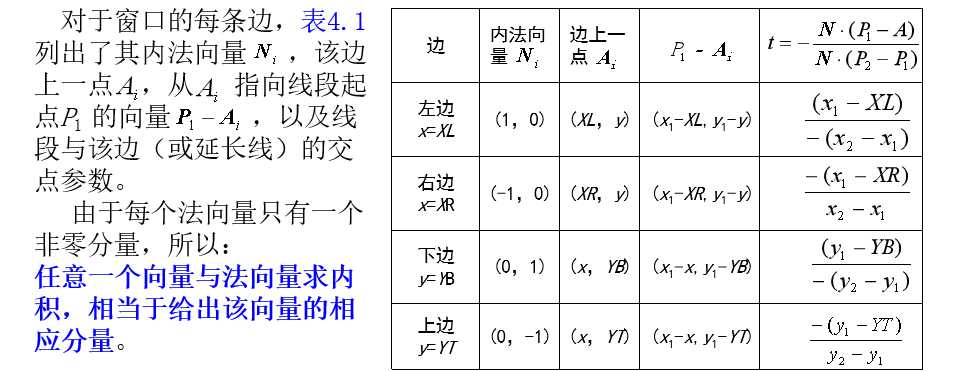

初始化线段在边界内的端点参数为ts=0、te=1。
计算出各个裁剪边界的r、s值。
当r=0且s<0时,舍弃该线段;否则计算线段与边界的交点参数t。
当r<0时,参数t用于更新ts;
当r>0时,参数t用于更新te。
如果更新了ts或te后,使ts>te,则舍弃该线段。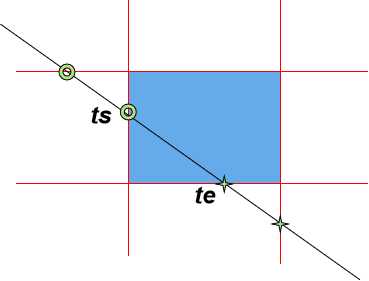

标签:color 一条直线 更新 char and 第一步 数值 The 进入
原文地址:https://www.cnblogs.com/wkfvawl/p/11704803.html