标签:例题 状态 递增 变化 eof poj clu 基本 logs
单调栈的基本应用2是单调栈的基本应用1的延伸。应用2主要解决的是二维平面的一些问题。
虽然已经应用到二维平面,但是单调栈的思想并没有变化
更多应用的是延伸的位置。本质是ai的左/右第一个大于ai的元素位置
下面列举的一些平面内单调栈的例题:
题目描述:
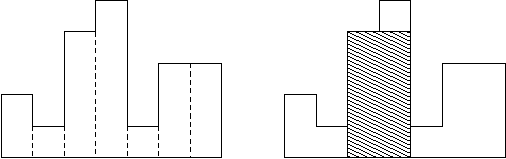
给定n个依次排列并且面积为1*hi的矩形,现求这个图形所包含最大的矩形的面积。
上图中7个矩形的h依次为2 1 4 5 1 3 3。注意题目有多组数据读入。
思路:
我们构造一个单调上升栈。这样,我们只需要在这个元素出栈时统计答案。
栈顶元素不断被弹出时,由于栈的单调性,我们记录变量Spread为栈顶元素能延伸的最大宽度。Spread+=Stack[top]来更新下一个会被弹出的元素的最大延伸距离。我们同时也需要更新最大的矩形面积。
当while循环结束后,将新元素入栈并更新下一个元素的延伸宽度(不更新所造成的后果稍经思考便能得出)。扫描完毕后,栈内仍可能会有剩余的单调上升元素。我们只需要对每个元素分别统计答案就可以了。
需要注意的是,Spread只统计本次新元素加入后栈内元素的延伸情况,在下一次新元素加入时Spread需要归0。
代码如下:
#include<iostream>
#include<cstdlib>
#include<cstdio>
#define N 100010
typedef long long ll;
using namespace std;
struct node{
int h,w;
}Stack[N];
int main()
{
int n,h;ll top,ans,spread;
while(scanf("%d",&n)&&n){
ans=top=spread=0;
for(int i=1;i<=n;i++){
scanf("%d",&h);
spread=0;//注意初始化!
while(top&&Stack[top].h>=h){//维护一个单调上升栈
//栈顶元素无法在保证其高度的情况下继续延伸
ll size=Stack[top].h*(Stack[top].w+spread);
//栈顶出栈时统计最大面积
spread+=Stack[top].w;
ans=max(ans,size);
//题目要求求出最大面积
top--;
}
Stack[++top].h=h;//入栈
Stack[top].w=spread+1;//此时累加栈顶元素延伸的长度
}
spread=0;
while(top){//对栈内剩余元素的处理
//栈已经有单调性,所以每次只需要不断出栈,累加延伸长度,统计答案就可以了
ll size=Stack[top].h*(Stack[top].w+spread);
ans=max(ans,size);
spread+=Stack[top].w;
top--;
}
printf("%lld\n",ans);
}
return 0;
}题目描述:给定一个n*m的矩形。现在让你求出该矩阵中所有"."能组成的矩形的总数量。
思路:
这道题很难会想出单调栈的做法。本题基本思路例1基本一致。
首先用前缀和处理出每列"."的和,当出现字符"*"时前缀和归零。接下来,对于每行我们都进行单调栈处理。
我们分别从l~r和r~l进行扫描,分别求出ai向右和向左最大能延伸到的位置。即g1和g2。
现在我们处理完了g1和g2,那么如何统计答案呢?这里涉及一点乘法原理,我们可以知道每个位置所贡献的答案就是(g1[i]-j)*(j-g2[i])*sum[i]
本题最大的细节问题在于答案的统计,需要注意重复计算答案的问题,请注意sum[st[top]]>sum[i]和sum[st[top]]>=sum[i]区别。
代码如下:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
char ch[1010][1010];
int n,m,sum[1010],a[1010][1010],st[1010],g1[1010],g2[1010];
ll ans;
inline void Spread(){
memset(g1,0,sizeof(g1));
memset(g2,0,sizeof(g2));
int top=0;
for(int i=1;i<=m;i++){
while(top&&sum[st[top]]>sum[i]){
g1[st[top]]=i;top--;//向右延伸
}
st[++top]=i;
}
while(top){g1[st[top]]=m+1;top--;}//此时元素最小,最远可以延伸到m+1
for(int i=m;i>=1;i--){
while(top&&sum[st[top]]>=sum[i]){//注意可以延伸的范围
g2[st[top]]=i;top--;//向左延伸
}
st[++top]=i;
}
while(top){g2[st[top]]=0;top--;}//此时元素最小,最远可以延伸到0
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%s",ch[i]+1);
for(int j=1;j<=m;j++){
if(ch[i][j]=='W') sum[j]++;
else sum[j]=0;
}
Spread();
for(int j=1;j<=m;j++)//统计答案
ans+=(g1[j]-j)*(j-g2[j])*sum[j];
}
printf("%lld",ans);
return 0;
}题目描述:略
思路:
本题为双倍经验题,解题思路与例二一致。
只是由矩形变换为正方形。
代码:略
当解决以上矩形类的问题时,一开始可能会找不到头绪。
但是经过简单的模拟可以发现,这些题都是在求序列中元素左、右以及左和右的延伸状态。
由此联想到单调栈,构造一个单调递增栈来求出元素左右第一个值小于它的位置。
这样问题便解决了,视具体情况使用单调栈可以很好地解绝时间复杂度的问题。
以上便是单调栈的基本应用,如果还有其他应用,我会继续更新的。
标签:例题 状态 递增 变化 eof poj clu 基本 logs
原文地址:https://www.cnblogs.com/cyanigence-oi/p/11707068.html