标签:高斯分布 logistic 最小值 因此 运算 局部最优 结果 求导 inf
一些神经元的输出会变成另外一些神经元的输入,一般以层来组织,最常见的是全连接神经网络,其中两个相邻层中每一个层的所有神经元与另一个层的所有神经元相连,每个层内部的神经元不相连。
一般的,N层神经网络并不会把输入层算进去,因此一个一层的神经网络是指没有隐藏层,只有输入层和输出层的神经网络。Logistic回归就是一个一层的神经网络。
输出层一般没有激活函数,因为输出层通常表示一个类别的得分或者回归的一个实值的目标,所以输出层可以是任意的实数。
在数据不太复杂时,容量较小的模型反而有着更好的效果,但是,很难衡量到到底多小的模型才算是小的模型,其次小的模型在使用如梯度下降法等训练的时候通常更难。因为神经网络的损失函数一般是非凸的,容量小的网络更容易陷入局部极小点而达不到最优的效果,同时,这些局部最小点的方差特别大。换句话说,也就是每个局部最优点的差异都特别大,所以在训练网络的时候训练10次可能得到的结果有很大的差异。但是对于容量更大的神经网络,它的局部极小点的方差特别小,也就是说训练多次虽然可能陷入不同的局部极小点,但是他们的差异很小,这样训练就不会完全依靠随机初始化。
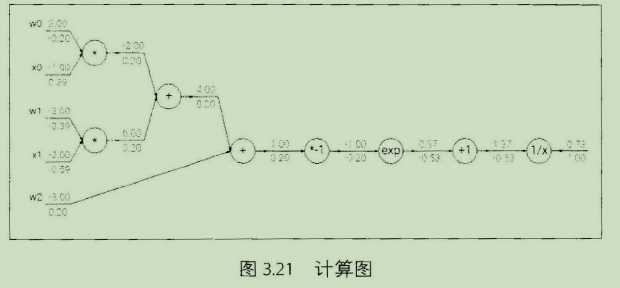
是一个有效的求解梯度的算法,本质其实就是一个链式求导法则的应用。链式法则:如果需要对其中的元素求导,那么可以一层一层求导,然后将结果乘起来,这就是链式法则的核心,也是反向传播算法的核心。
直观上看反向传播算法是一个优雅的局部过程,每次求导只是对当前的运算求导,求解每层网络的参数都是通过链式法则将前面的结果求出不断迭代到这一层的,所以说这是一个传播过程。
sigmoid函数举例:
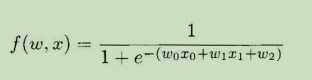

1.SGD
2.Momentum:随机梯度下降的同时,增加动量,动量的计算基于前面梯度,参数更新不仅仅基于当前的梯度,也基于之前的梯度。
3.Adagrad:自适应学习率的方法。学习率不断变小,且受每次计算出来的梯度影响,对于梯度比较大的参数,它的学习率就会变得相对更小。
1.中心化:每个特征维度都减去相应的均值实现中心化,这样可以使数据变成0均值。
2.标准化:数据不同的特征维度都有着相同的规模。一种是除以标准差,这样可以使新数据的分布接近标准高斯分布,另外一种是每个特征维度的最大值和最小值按比例缩放到-1到1之间。
3.PCA
4.白噪声:首先跟pca一样将数据投影到一个特征空间,然后每个维度除以特征值来标准化这些数据,直观上就是一个多元高斯分布转换到了一个0均值,协方差矩阵伪1的多元高斯分布。白噪声会增强数据中的噪声,因为其增强了数据中的所有维度,包括了一些方差很小的不相关的维度。
1.正则化:

2,Dropout
标签:高斯分布 logistic 最小值 因此 运算 局部最优 结果 求导 inf
原文地址:https://www.cnblogs.com/shuangcao/p/11718478.html