标签:应该 概率 反向 消失 机器学习 实例 分类 激活 bsp
转自https://blog.csdn.net/qq_42823043/article/details/89765194
简介
Batch Normalization简称BN,是2015年提出的一种方法《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》,已经广泛被证明其有效性和重要性。虽然有些细节处理还解释不清其理论原因,但是实践证明好用才是真的好。
原论文地址:https://arxiv.org/abs/1502.03167
机器学习领域有个很重要的假设:IID独立同分布假设,就是假设训练数据和测试数据是满足相同分布的,这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。而BN就是在深度神经网络训练过程中使得每一层神经网络的输入保持相同分布的。
为什么深度神经网络随着网络深度加深,训练起来越困难,收敛越来越慢?这是个在DL领域很接近本质的好问题。很多论文都是解决这个问题的,比如ReLU激活函数,再比如ResNet等,BN本质上也是解释并从某个不同的角度来解决这个问题的。
一、Internal Covariate Shift 现象:
从论文名字可以看出,BN是用来解决“Internal Covariate Shift”问题的。首先来解释一下什么叫做covariate shift现象,这个指的是训练集的数据分布和预测集的数据分布不一致,这样的情况下如果我们在训练集上训练出一个分类器,肯定在预测集上不会取得比较好的效果。这种训练集和预测集样本分布不一致的问题就叫做“covariate shift”现象。
对于深度学习这种包含很多隐层的网络结构,在训练过程中,因为各层参数不停在变化,所以每个隐层都会面临covariate shift的问题。也就是在训练过程中,隐层的输入分布老是变来变去,导致网络模型很难稳定的学规律,这就是所谓的“Internal Covariate Shift”,Internal指的是深层网络的隐层,是发生在网络内部的事情,而不是covariate shift问题只发生在输入层。
二、Batch Normalization 由来:
针对上述问题,于是提出了BatchNorm的基本思想:能不能让每个隐层节点的激活输入分布固定下来呢?这样就避免了“Internal Covariate Shift”问题了。
启发来源:之前的研究表明如果在图像处理中对输入图像进行白化(Whiten)操作的话(所谓白化,就是对输入数据分布变换到0均值,单位方差的正态分布)那么神经网络会较快收敛。
那么BN作者就开始推论:图像是深度神经网络的输入层,做白化能加快收敛,那么其实对于深度网络来说,其中某个隐层的神经元是下一层的输入,意思是其实深度神经网络的每一个隐层都是输入层,不过是相对下一层来说而已,那么能不能对每个隐层都做白化呢?所以BN可以理解为对深层神经网络每个隐层神经元的激活值做简化版本的白化操作。
三、Batch Normalization 原理:
BN的基本思想其实相当直观:因为深层神经网络在做非线性变换前的激活输入值x随着网络深度加深或者在训练过程中,其分布逐渐发生偏移或者变动,之所以训练收敛慢,一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近,所以这导致反向传播时低层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因。
而BN就是通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布,其实就是把越来越偏的分布强制拉回比较标准的分布,这样使得激活输入值落在非线性函数对输入比较敏感的区域,这样输入的小变化就会导致损失函数较大的变化,意思是这样让梯度变大,避免梯度消失问题产生,而且梯度变大意味着学习收敛速度快,能大大加快训练速度。
上面说得还是显得抽象,下面更形象地表达下这种调整到底代表什么含义:
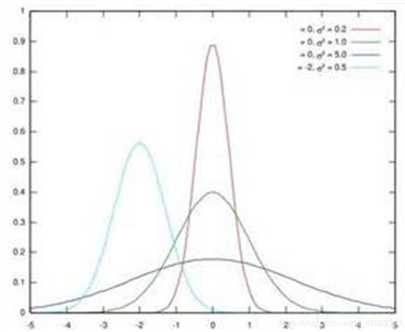
假设某个隐层神经元原先的激活输入x取值符合正态分布,正态分布均值是-2,方差是0.5,对应上图中最左端的浅蓝色曲线,通过BN后转换为均值为0,方差是1的正态分布(对应上图中的深蓝色图形)。这意味着输入x的取值正态分布整体右移2(均值的变化),图形曲线更平缓了(方差增大的变化)。那么把激活输入x调整到这个正态分布有什么用?首先我们看下均值为0,方差为1的标准正态分布代表什么含义:
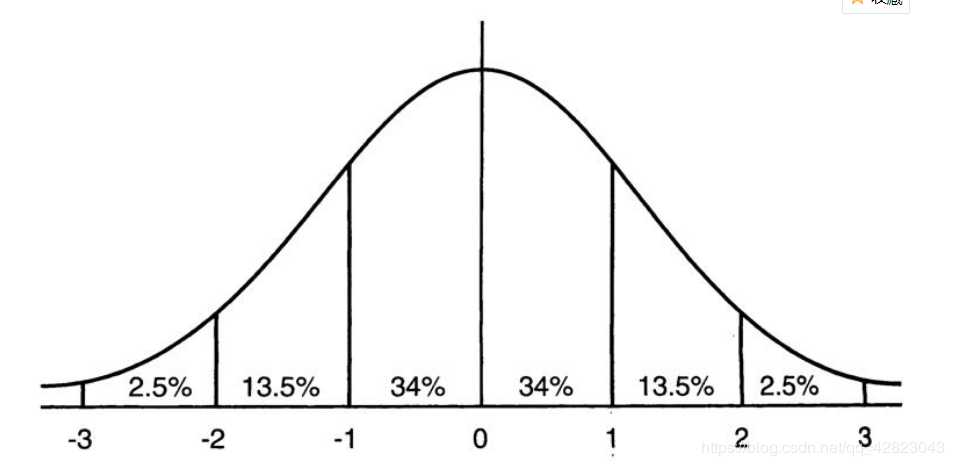
这意味着在一个标准差范围内,也就是说64%的概率x其值落在[-1,1]的范围内,在两个标准差范围内,也就是说95%的概率x其值落在了[-2,2]的范围内。那么这又意味着什么?我们知道,激活值x=WU+B,U是真正的输入,x是某个神经元的激活值,假设非线性函数是sigmoid,那么看下sigmoid(x)函数及其导数:
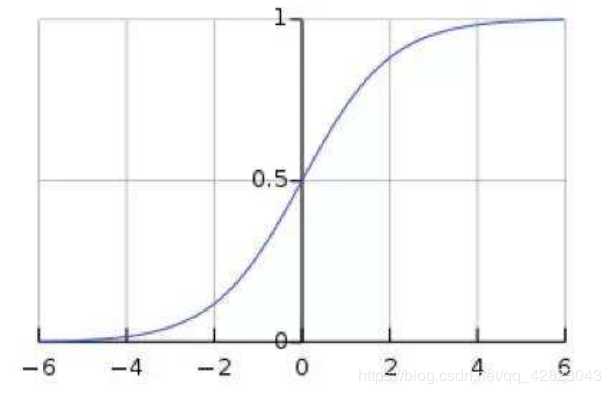
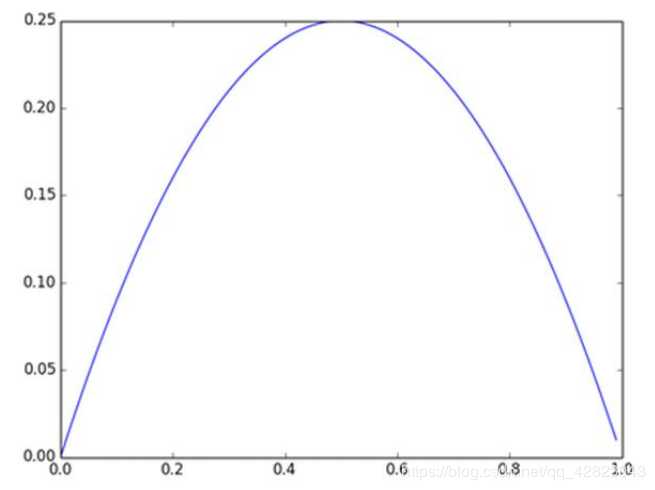
所以经过BN后,均值是0,方差是1,那么意味着95%的x值落在了[-2,2]区间内,很明显这一段是sigmoid(x)函数接近于线性变换的区域,意味着x的小变化会导致非线性函数值较大的变化,也即是梯度变化较大,对应导数函数图中明显大于0的区域,就是梯度非饱和区。
也就是说
经过BN后,目前大部分Activation的值落入非线性函数的线性区内,其对应的导数远离导数饱和区,这样来加速训练收敛过程。
到了这里,又会发现一个问题:如果都通过BN,那么不就跟把非线性函数替换成线性函数效果相同了?我们知道,如果是多层的线性函数变换其实这个深层是没有意义的,因为多层线性网络跟一层线性网络是等价的。这意味着网络的表达能力下降了,这也意味着深度的意义就没有了。所以BN为了保证非线性的获得,对变换后的满足均值为0方差为1的x又进行了scale加上shift操作(y=scale*x+shift),每个神经元增加了两个参数scale和shift参数,这两个参数是通过训练学习到的,意思是通过scale和shift把这个值从标准正态分布左移或者右移一点并长胖一点或者变瘦一点,每个实例挪动的程度不一样,这样等价于非线性函数的值从正中心周围的线性区往非线性区动了动。核心思想应该是想找到一个线性和非线性的较好平衡点,既能享受非线性的较强表达能力的好处,又避免太靠非线性区两头使得网络收敛速度太慢。当然,论文作者并未明确这样说。
四、Batch Normalization 算法流程:
上面是对BN的抽象分析和解释,具体在Mini-Batch SGD下做BN怎么做?其实论文里面这块写得很清楚也容易理解。
在多层CNN里,BN放在卷积层之后,激活和池化之前,以LeNet5为例:
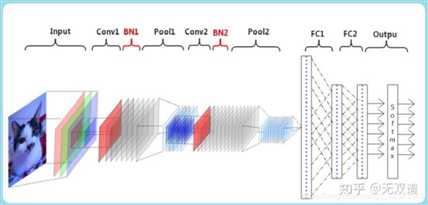
对于Mini-Batch SGD来说,一次训练过程里面包含m个训练实例,其具体BN操作就是对于隐层内每个神经元的激活值来说,进行如下变换:
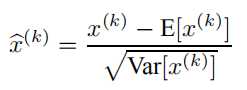
变换的意思是:某个神经元对应的原始的激活x通过减去mini-Batch内m个实例获得的m个激活x求得的均值E(x)并除以求得的方差Var(x)来进行转换。
上文说过经过这个变换后会导致网络表达能力下降,为了防止这一点,每个神经元增加两个调节参数(scale和shift),这两个参数是通过训练来学习到的,用来对变换后的激活反变换,使得网络表达能力增强,即对变换后的激活进行如下的scale和shift操作,这其实是变换的反操作:
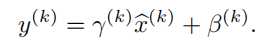
这就是算法的关键之处了,每一个神经元x都会有这样的一对参数,当:
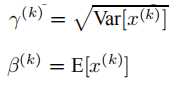
这样的时候可以恢复出原始的某一层学习到的特征的,因此我们引入这个可以学习的参数使得我们的网络可以恢复出原始网络所要学习的特征分布,最后BN层的前向传导公式为:

上面公式中的m指的是mini-batch size。也就是每一个batch来做一个这样的BN。代码对应也是四句话:

五、BN带来的好处:
没有它之前,需要小心的调整学习率和权重初始化,但是有了BN可以放心的使用大学习率;
极大提升了训练速度,收敛过程大大加快;
Batch Normalization本身上也是一种正则的方式,可以代替其他正则方式如Dropout等。
六、BN的缺陷:
Batch Normalization中的batch就是批量数据,即每一次优化时的样本数目,通常BN网络层用在卷积层后,用于重新调整数据分布。假设神经网络某层一个batch的输入为X=[x1,x2,…,xn],其中xi代表一个样本,n为batch size。
当batch值很小时,计算的均值和方差不稳定。研究表明对于ResNet类模型在ImageNet数据集上,batch从16降低到8时开始有非常明显的性能下降。所以BN不适应于当训练资源有限而无法应用较大的batch的场景。
注:参考知乎各位大佬深度学习中 Batch Normalization为什么效果好?和郭耀华大神【深度学习】深入理解Batch Normalization批标准化
标签:应该 概率 反向 消失 机器学习 实例 分类 激活 bsp
原文地址:https://www.cnblogs.com/scarecrow-blog/p/11721259.html