标签:怎样 真实机 count 排除 计时器 设置 字符串 方案 整数
我们所用的程序设计语言都必须反映出计算机能够执行的操作类型。让我们通过重述计算机的定义来开始新的讨论:计算机是能够存储、检索和处理数据的可编程电子设备。
这个定义中的操作字包括可编程的、存储、检索和处理。上一章指出了数据和操作数据的指令逻辑上是相同的,它们存储在相同的地方。这就是“可编程的”这个词的意义所在。操作数据的指令和数据一起存储在机器中。要改变计算机对数据的处理,只需要改变指令即可。
存储、检索和处理是计算机能够对数据执行的动作。也就是说,控制单元执行的指令能够把数据存储 到机器的内存中,在机器内存中检索数据,在算术逻辑单元中以某种方式处理数据。词语“处理”非常通用。在机器层,处理涉及在数据值上执行算术和逻辑操作。
机器语言:由计算机直接使用的二进制编码指令构成的语言
虚拟机:为了模拟真实机器的重要特征而设计的假想机器
回忆第5章中所说的,寄存器是中央处理器中算术/逻辑单元的一小块存储区域,它用来存储特殊的数据和中间值。Pep/8有七个寄存器,我们重点研究其中三个:
累加器是用来保存操作的数据和结果。累加器是一种特殊的存储寄存器。
一个字节能够表示的最大十进制数是255,用二进制表示是111111,用十六进制表示是FF。一个字(16位)能够表示的最大十进制数是65535,用二进制表示是1111111111111用十六进制表示是FFFF。如果既要表示正数,又要表示负数,那么在量级上就会少一位(因为有一位用于表示符号),因此可以表示的十六进制值数的范围约为-7FFF到+7FFF,相当于十进制数的-32767到+32767。 当我们使用Pep/8虚拟机时,这一信息是十分重要的。
可用的比特数决定了我们可以使用的内存大小。
我们说过,指令要先进入指令寄存器,然后经过译解,最后被执行。接下来,让我们仔细研究一套计算机能够执行的具体指令。首先,我们需要分析Pep/8 中的指令格式。
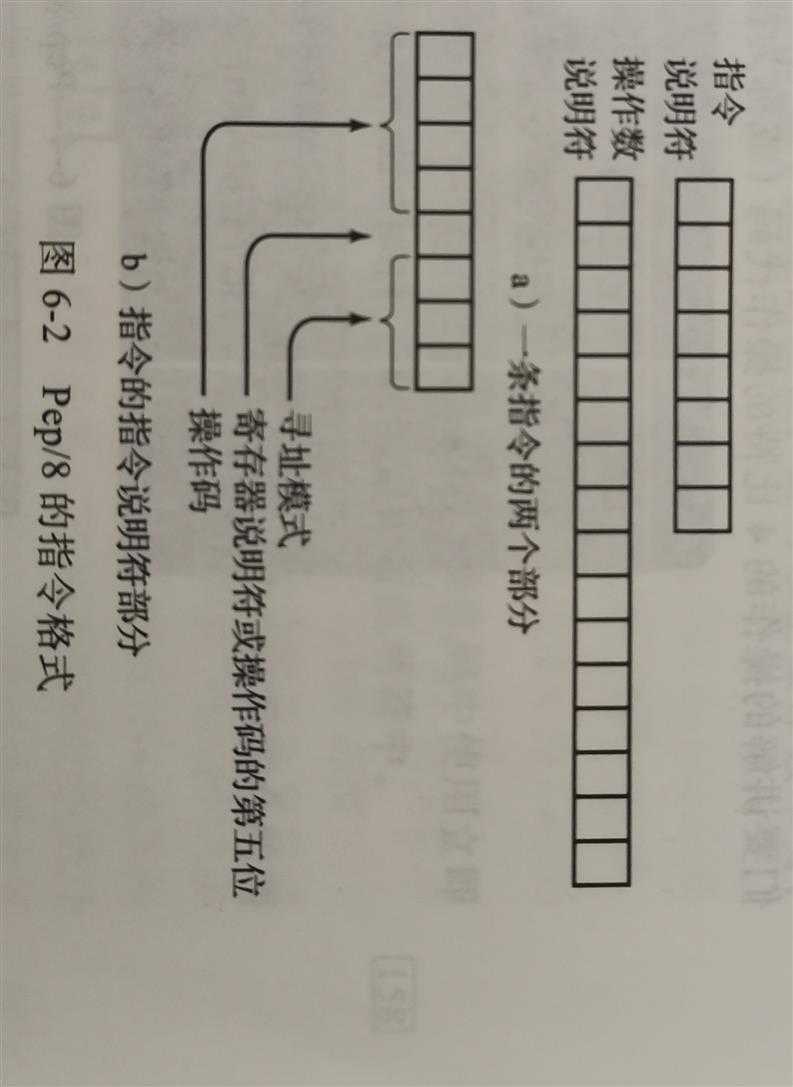
图6-2a展示了Pep/8中的指令格式。一条指令由两部分组成,即8位的指令说明符和(可选的)16位的操作数说明符。指令说明符(指令的第一个字节) 说明了要执行什么操作(如把一个数加到一个已经存储在寄存器中的值上)和如何解释操作数的位置。操作数说明符(指令的第二和第三个字节)存放的是操作数本身或者操作数的地址。有些指令没有操作数说明符。
指令说明符的格式根据表示一个具体操作所用的比特数的不同而不同。在Pep/8中,操作代码(称为操作码)的长度从4比特到8比特不等。我们在这里所用的操作码长度是4比特或5比特,4比特操作码的第5位用来指定使用哪个寄存器。寄存器A(累加器)的寄存器说明符是0,这是唯一一个我们要用到的寄存器。(请参见图6-2b。)
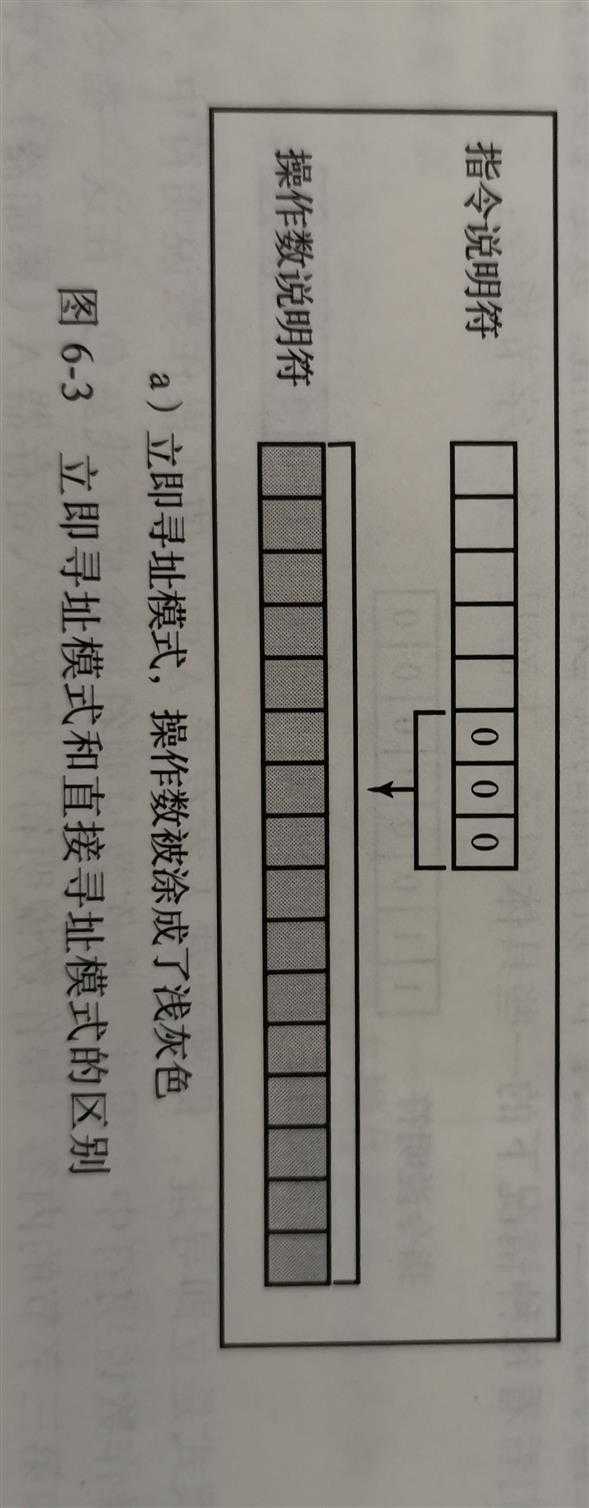
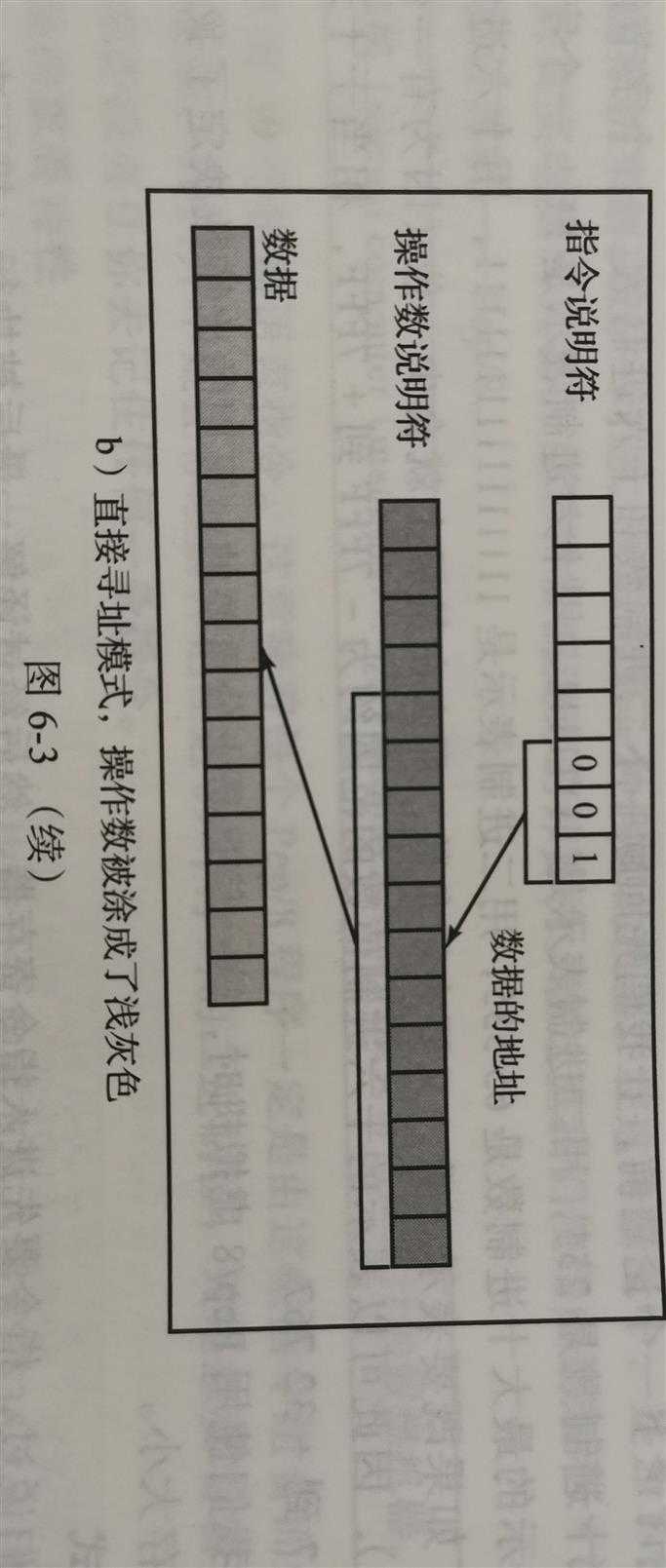
3比特 的 寻址模式说明符 表示了怎样解析指令中的操作数部分。如果寻址模式是000 ,那么指令的操作数说明符中存储的就是操作数 。这种寻址模式称为立即寻址(i) 。 如果寻址模式是001 ,那么操作数说明符中存储的是操作数所在的内存地址名称 。这种寻址模式称为直接寻址(d) 。
立即寻址模式和直接寻址模式之间的差别十分重要,因为它决定了操作中涉及的数据存储或将要被存储的位置 。请参见图6-3。
没有操作数(要处理的数据)的指令称为一元指令,这些指令没有操作数说明符。即,一元指令的长度是1个字节,而不是3个字节。

装入程序:软件用于读取机器语言并把它载入内存的部分
汇编器:把汇编语言程序翻译成机器代码的程序
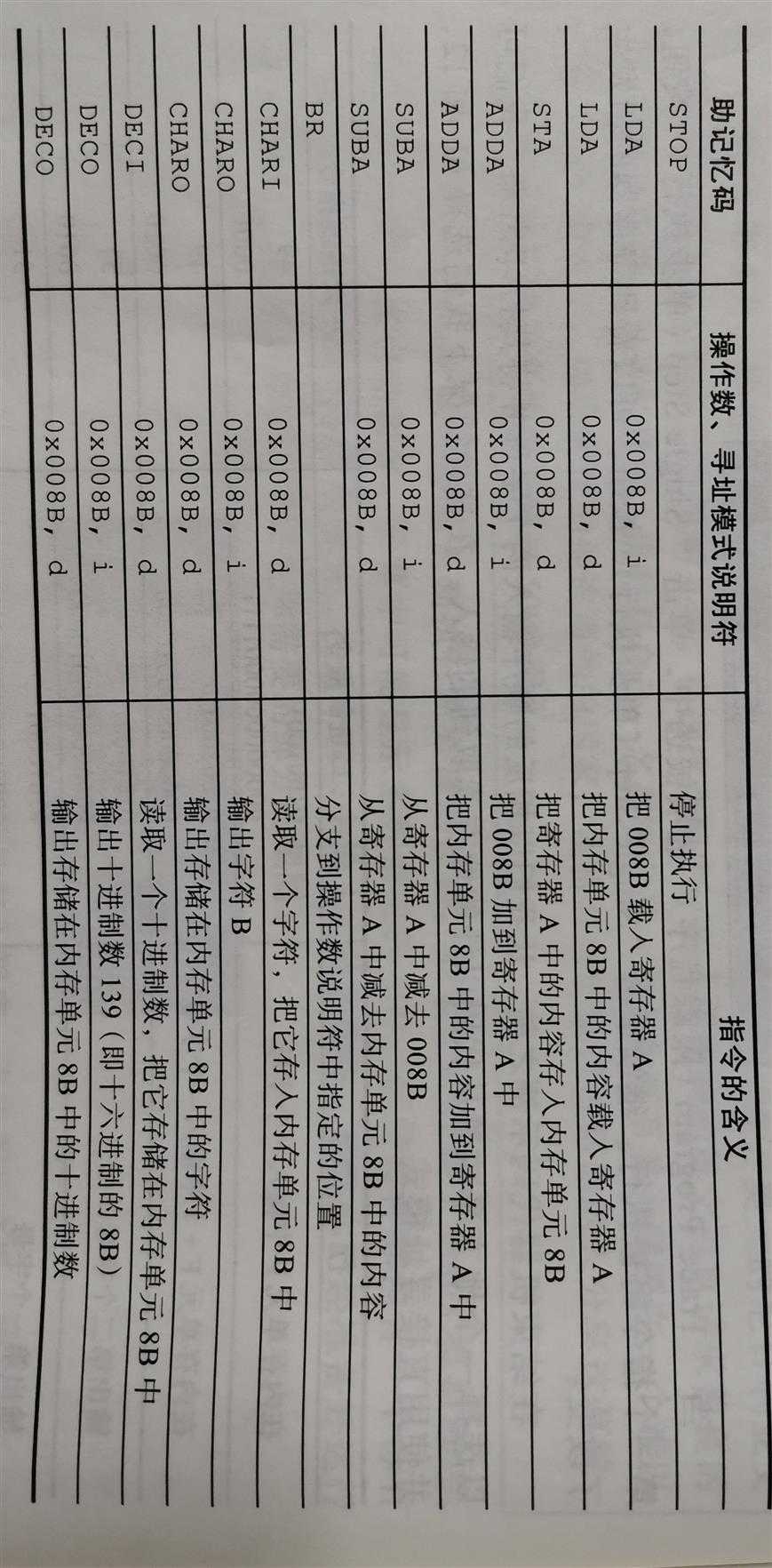
汇编指令:翻译程序使用的指令
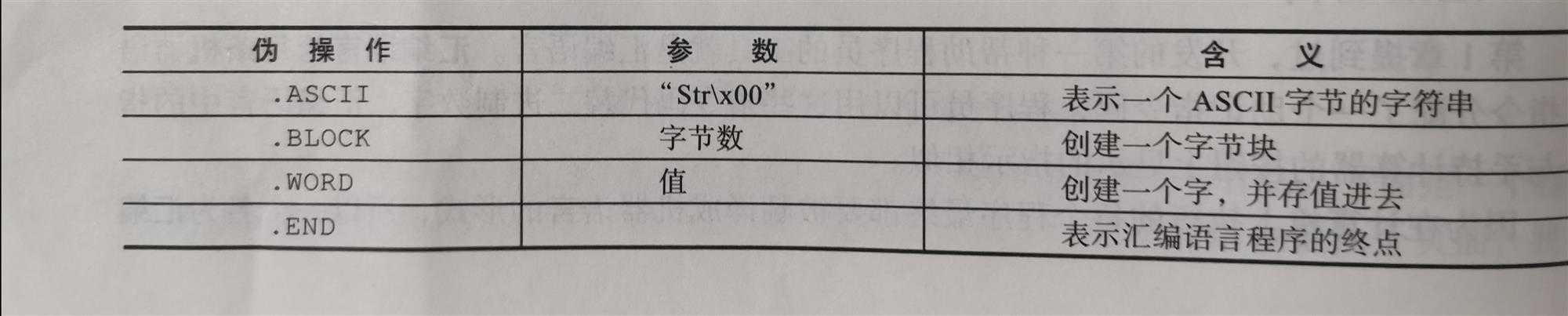
下面是Pep/8汇编器中的几条有用的汇编器指令:
注释:为程序读者提供的解释性文字
(编译器会忽略从分号开始到一行结束的所有字符,这就是一个注释)
运行一个汇编语言程序的过程如图6-5所示。汇编器的输入是一一个用汇编语言编写的程序,输出是用机器代码编写的程序。你可以看到为什么汇编语言的出现是编程语言的发展中如此重要的一步: 它通过将指令抽象为单词,从而删除了机器语言编程的很多细节。
虽然在执行一个程序时增加了一个步骤(汇编语言翻译成机器代码),但是这个额外的步骤是非常值得的,这大大简化了程序员的工作。
伪代码:一种表达算法的语言
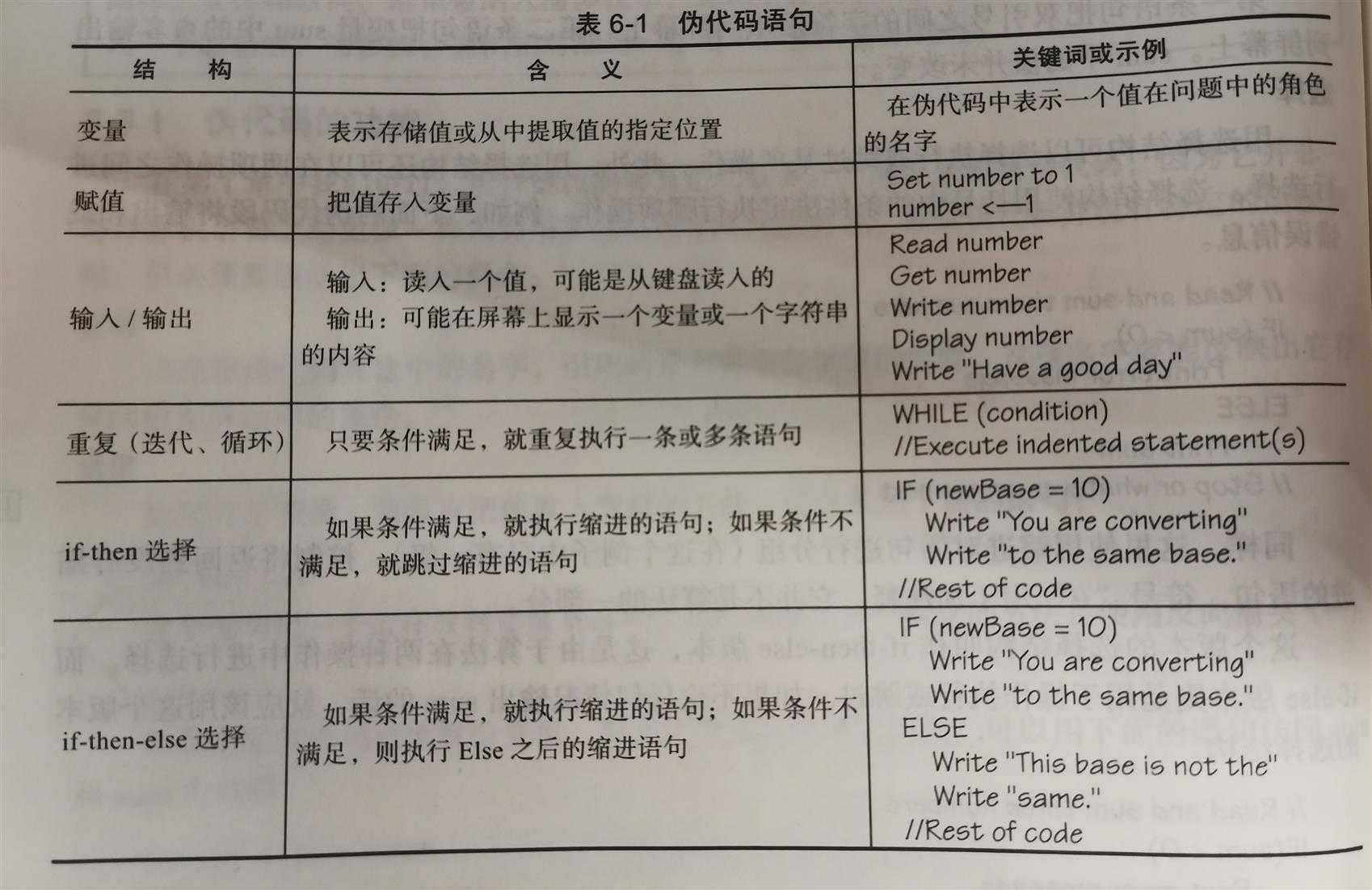
出现在伪代码算法中的名字,引用的是内存中存储值的位置。这些名字要能反映出它存放的值在算法中的角色
如果有了变量,就要有把值放入变量的办法。
可以采用下面的语句:
Set sum to 0 & sum <—— 1
这个语句把一个值存放到变量sum中。
如果用赋值语句把值赋给变量,那么之后如何访问它们呢?可以用下面的语句访向sum和num中的值:
Set sum to sum + num或sum <一sum + num
存放在sum中的值加上存放在num中的值,结果存放在sum中。因此,当变量用于“to”或者“←”右边时,就能访问变量的值。当变量用于“Set” 后或“←”的左边时,就会向其中存人一个值。
存入变量的值可以是单个的值(如0),也可以是由变量或操作符构成的表达式(如 sum + num)。
大多数计算机程序只处理某种类型的数据,所以必须能够从外部世界向计算机中输入数据值,还要能把结果输出到屏幕上。我们可以使用Write语句进行输出,使用Read语句进行输入。
Write“Enter the number of values to read and sum”
Read num
双引号之间的字符叫作*字符串*,它们告诉了用户要输入什么或者要输出什么。究竟采用Display还是Print是无关紧要的,它们都等价于Write, Get和Input都与Read同义。记住,伪代码算法是写给人们看的,以便之后可以把它们转换成程序设计语言。不仅对于你自己,对于要理解你所写的算法从而把它转换成程序的其他人来说,在一个项目中保持使用一致的单词是一种好习惯。
最后两个输出语句说明了重要的一点:
Write“Err”
Write sum
第一条语句把双引号之间的字符输出到屏幕上,第二条语句把变量sum中的内容输出到屏幕上。sum中的值并未改变。
用选择结构可以选择执行或跳过某项操作。此外,用选择结构还可以在两项操作之间进行选择。选择结构使用括号中的条件决定执行哪项操作。例如,下面的伪代码段将输出和或错误信息。
// Read and sum three numbers
IF (sum< 0)
??Print error message
ELSE
??Print sum
// Stop or whatever comes next
同样,这里使用缩进对语句进行分组(在这个例子中只有一组)。控制将返回到没有缩进的语句。符号“//” 用于加注释,它并不是算法的一部分。
这个版本的选择结构叫作if-then-else版本,这是由于算法在两种操作中进行选择。而if-else版本则是用于操作执行或跳过。如果不论任何情况输出sum的话,就应该用这个版本的选择结构。
// Read and sum three numbers
IF(sum< 0)
??Print error message
Print sum
// Stop or whatever comes next
使用重复结构可以重复执行指令。比如在求和问题中,计数器被初始化、检验并增加。伪代码允许我们概述算法,所以这部分就变得易于理解。和选择结构一样,在WHILE旁边的圆括号中的表达式是一个判断,如果判断成立,缩进中的语句将被执行,如果不成立,就会跳过缩进中的语句,直接执行下一一个非缩进语句。
Set limit to number of values to sum
WHILE (counter < limit)
??Read num
??Set sum to sum + num
??Set counter to counter + 1
//Rest of program
WHILE和IF旁边的括号里的表达式是布尔表达式,其结果可为真或假。在IF中,如果表达式为真,则执行接下来的缩进代码块块,若表达式为假,则跳过缩进代码块。在WHILE中,如果表达式为真,则执行缩进代码块。如果表达式为假则跳到下一个不缩进的执行语句。将WHILE、IF和ELSE大写是因为这些语句通常直接使用在很多编程语言中,在计算领域中它们有特殊的含义。
伪代码最终必须被翻译成可在计算机上运行的程序。一个伪代码语句可以被翻译成多种汇编语言语句,但是只能被翻译成一种高级语言。
把十进制数字系统转化为其他进制数字的算法表达为伪代码形式
在写算法的过程中,我们采用了2个主要的策略。我们问了问题并推迟了细节 。问问题是我们大多数人都熟悉的策略。推迟细节则是首先给任务-一个名称,然后再补充细节来完成这个任务。也就是说,我们首先用more pairs 和print them in order 来编写算法代码,然后补充细节以完成这个任务。这种的策略被称为分步解决。
在没有测试之前,算法都不算完成。可以采用基于模拟基数转换算法的方法来测试算法:可以选择数值,用纸和笔进行代码走查。这一过程叫作桌面检查 。我们坐于桌前,用笔和纸走查整个设计。在推理设计时,采用真实的数值来跟踪发生的情况非常有用。这个方法虽然简单,但却极其有效。
测试计划(test plan):说明如何测试程序的文档。
代码覆盖(明箱)测试法(code-coverage (clear-box) testing): 通过执行代码中的所有语句测试程序或子程序的测试方法。
数据覆盖(暗箱)测试法(data-coverage (black-box) testing):把代码作为一个暗箱,基于所有可能的输人数据测试程序或子程序的测试方法。
测试计划实现( test-plan implementation) :用测试计划中规定的测试用例验证程序是否输出了预期的结果。

下面是一些你应该问的典型问题:
我如何知道已经找到解决方案了?
永远不要彻底重新做件事*。 如果解决方案已经存在了,就用这种方案。如果以前曾经解决过相同或相似的问题,只需要再次使用那种成功的解决方案即可。通常,我们意识不到“我以前见过这种问题,我知道该如何处理它”,而只是苦苦求索。人类是擅长识别相似的情况的。我们根本不必学习如何去商店买牛奶,然后买鸡蛋,再买糖果。我们知道,去商店购物这件事都是一样的,只是买的东西不同罢了。
识别相似的情况在计算领域内是非常有用的。在计算领域中,你会看到某种问题不断地以不同的形式出现。一个好的程序员看到以前解决的任务或者任务的一部分(子任务)时,会直接选用已有的解决方案。例如,找出一个温度列表中每天的最高温和最低温与找出一个测验列表中的最高分和最低分是完全相同的任务,想得到的不过是一个数字集 合中的最大值和最小值而已。
这项原则尤其适用于计算领域:把大的问题分割成能够单独解决的小问题。
这种方法应用了第1章中讨论的抽象概念,可以把一项任务分成若干个子任务,而子任务还可以继续划分为子任务,如此进行下去。可以反复利用分治法,直到每个子任务都是可以实现的为止。
我们把这些策略应用到过去两个章节中遇到的问题并将细节推迟,设计算法读取两个数并按顺序输出它们。
Polya列表的第二步中的最后一句说,最终应该得到解决方案。在计算领域,这种解决方案被称为算法。
算法(algorithm):在有限的时间内用有限的数据解决问题或子问题的明确指令集合。
(这个定义暗示,算法中的指令是明确的。)
在计算领域中,必须明确地描述人类解决方案中暗含的条件。在计算机解决方案中必须明确这些限制,因此算法的定义包括它们。
Polya列表的第三步是执行解决方案,也就是测试它,看它是否能解决问题。第四步是分析解决方案,以备将来使用。

自顶向下的方法可以分解为四个主要步骤。
根据需要进行重组和改写
为变化做好打算。不要害怕从头来过。一些尝试和细化操作是必要的。要维持透明性。简单直接地表达你的想法。
与Polya问题求解策略相似的设计方式即为自顶向下设计,将任务分层从而解决。
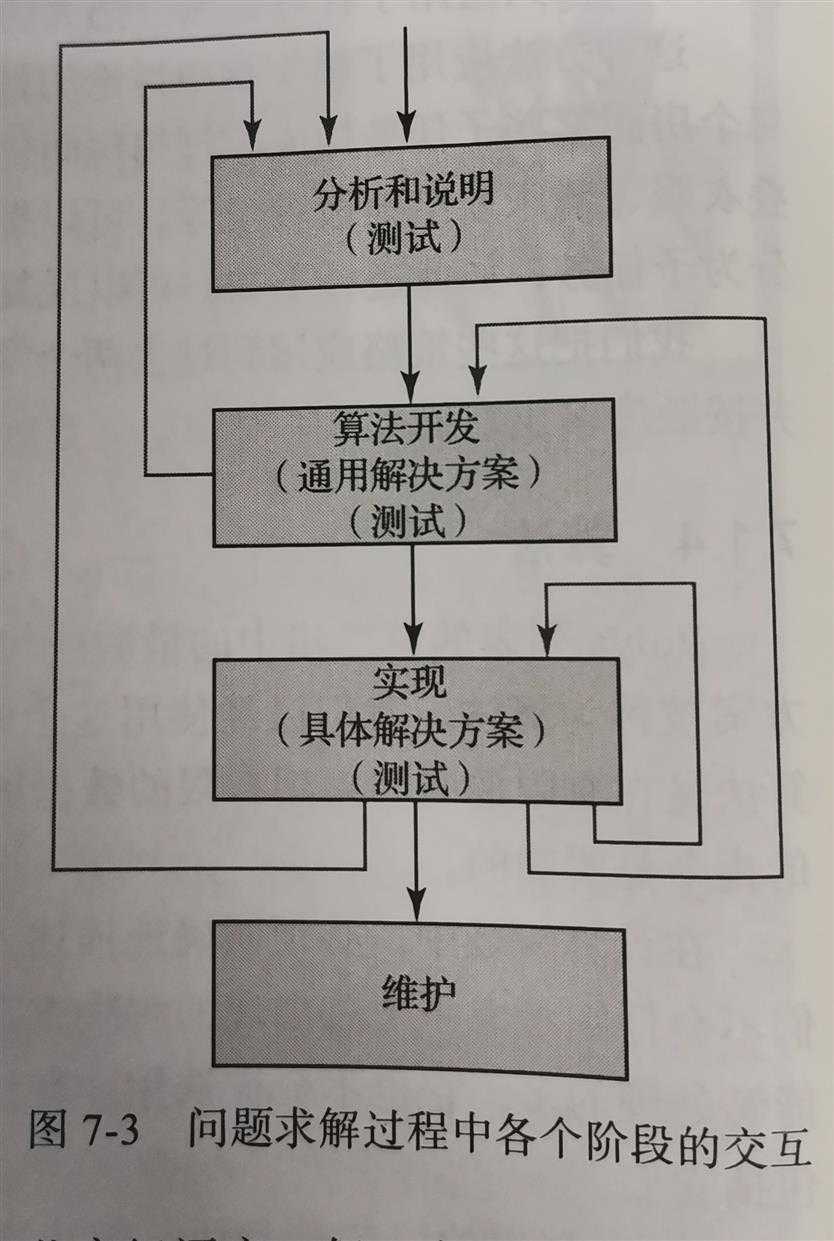
数学问题求解的目标是生成问题的特定答案,因此,检查结果等价于测试推出答案的过程。如果答案是正确的,过程就是正确的。但是,计算机问题求解的目标是创建正确的过区程。体现这一过程的算法可被反复应用到不同的数据,因此过程自身必须经过测试或验证。
算法的测试通常都是在编码算法的各种条件下运行程序,然后分析结果以发现问题。不过,这种测试只能在程序完成或至少部分完成时进行,这种测试太迟了,所以不能依赖。越早发现和修正问题,解决问题就越容易,代价也越小。
显然,需要在开发过程的更早阶段执行测试。特别是算法必须在实现之前进行测试。
简单(原子)变量是那些不能被分开的变量,是存储在一个地方的一个值。
例如根据温度选衣服:
IF(temperature>90)
??Write "Texas weather: wear shorts"
ELSE IF (temperature > 70)
??Write "Ideal weather: short sleeves are fine"
ELSE IF (temperature > 50)
??Write A lttle chilly: wear a light jacket"
ELSE IF (temperature > 32)
??Write "Philadelphia weather: wear a heavy coat"
ELSE
??Write "Stay inside"
计数控制循环可以指定过程重复的次数,这个循环的机制是简单记录过程重复的次数并且在重复再次开始前检测循环是否已经结束。
这类循环有三个不同的部分,使用一个特殊的变量叫作循环控制变量。第一部分是初始化:循环控制变量初始化为某个初始值。第二部分是测试:循环控制变量是否已经达到特定值? 第三部分是增量:循环控制变量以1递增。
循环控制变量count在循环外已被设置为0。测试表达式count-limit,如果表达式为真则执行循环。循环中的最后一句使得控制循环变量count递增。循环会执行多少次呢?循环执行时count为0,1, 2,…,limit-1。 因此,循环执行了limit次。循环控制变量的初始值和布尔表达式中的关系运算符共同确定了循环执行的次数。
while循环被称为前测试循环,因为在循环开始前就测试了。如果最初条件为假,将不进入循环。如果省略增量语句时会发生什么?布尔表达式从不改变。如果表达式开始时为假,那就什么也不会发生,循环也就不执行;如果表达式开始时为真,表达式将从不改变,所以循环将一直执行。实际上,大多数计算系统都有一个计时器,所以程序不会真的一直运行下去。相反,程序将停止于一条错误消息。永远不会终止的循环称为一个无限循环。
Pep/8使用分号来表明之后的部分是注释,而不是程序的一部分。在我们的伪代码中,使用两个斜杠来开始注释。
循环中重复的次数是由循环体自身内发生的事件控制的循环被称为事件控制循环。当使用while语句来实现事件控制循环时,这一过程仍分为三个部分: 事件必须初始化,事件必须被测试,事件必须更新。
计数控制循环是非常简单直接的,它指定了循环的次数,而在事件控制循环中则不太清楚,并不显而易见。
注意将选择控制结构嵌人循环中。在控制结构中执行或跳过的语句可以是简单的语句或者是复杂的语句(缩进语句块)————没有限制这些语句是什么。因此,跳过或重复的语句中可以包含一个控制结构。选择语句可以嵌套在循环结构中,循环结构可以嵌套在选择语句中。控制结构嵌入另个控制结构被称为嵌套结构。
嵌套结构( nested structure) :控制结构嵌人另一个控制结构的结构,又称为嵌套逻辑( nestedlogic)。
集体步骤:细节完全明确的算法步骤,不需要扩展
数组是同构项目的有名集合,可以通过单个项目在集合中的位置访问它们。项目在集合中的位置叫作索引。虽然人们通常从1开始计数,但多数程序设计语言从0开始,因此这里也采用这种方式。图7-5中是一个具有从0到9这10个元素的数组。
如果数组叫numbers,则通过表达式numbers[position]来访问数组中的每个值,其中position就是索引,是一个从0到9之间的数。
所以numbers就是一一个数组,通过在数组名后加上中括号并且括号中写上integer来保存整数值。在之前的算法中,我们没有列出变量,而是假设使用一一个变量名时这个变量是存在的。现在,我们使用的是复合结构,需要说明想要的是哪一种结构 。
与数组有关的算法分为三类:搜索、排序和处理。搜索 就像它的字面意思样,搜索数组中的项,一次寻找一个特定的值。排序 是按顺序将元素放人数组中。如果项是字符或字符串,将以字母顺序排序。一个已排序的数组中的项已经排好顺序。处理 是一种捕捉短语,包含了对数组中的项所做的所有其他计算。
记录是异构项目的有名集合,可以通过名字单独访问其中的项目。*所谓异构,就是指集合中的元素可以不必相同*。集合可以包含整数、实数、字符串或其他类型的数据。记录可以把与一个对象相关的各种项目绑定在一起。
二分检索:在有序列表中查找项目的操作,通过比较操作排除大部分检索范围
在计算机领域,把无序数组转化成有序数组是很常见的有用操作,好的排序算法非常受欢迎。
在排序中,从第一个数开始,在全体数据中寻找最小值,把最小值与比较值互换位置可以免去所需要的复制空间,直到所以数据排序完成。
从最后一个值开始,比较相邻的数进行交换或不交换操作,这个算法是非常慢的算法。需要对数组中除最后一个数之外的所以数进行一次迭代。(这里一次迭代意思是将正确的数字放到正确的位置为一次,其中有多次互换。)
但是,比较冒泡排序法和选择排序法对一个有序数组的操作。选择排序算法不能确定数组是否是有序的,因此,一定要执行整个算法。
当在一个算法中使用它自己时,这样的算法被称为递归算法。如果在某种程度上调用自己,则这个调用称为递归 调用。递归就是算法调用它本身的能力,是另一种重复(循环)的控制结构。这种算法使用一个选择语句来确定是否重复算法来调用一遍或停止这一过程,而不是使用一个循环语句执行一个算法。
递归(recursion)算法调用它本身的能力。
每个递归算法至少有两种情况:基本情况 和一般情况。基本情况是答案已知的情况;一般情况则是调用自身来解决问题的更小版本的解决方案。因为一般情况下解决的是原始问题越来越小的版本,所以程序最终达到基本情况,即答案是已知的,所以递归停止。
与每个递归问题相关的是如何衡量问题的大小。每次递归调用后,问题都应该减小。所有递归解决方案的第一步 都是确定尺寸系数 。如果问题涉及的是数值,尺寸系数可能就是数值本身。如果问题涉及结构,那么尺寸系数可能就是结构的尺寸。
到目前为止,我们先给每一层中的任务一个名字,然后在下一层展开这个任务,在最终的算法中收集所有碎片。使用递归算法时,每次执行算法提供给算法的数据值必须是不同的。因此,继续递归之前,先要了解一个新的控制结构:子程序语句。虽然我们仍在算法层面,但这个控制结构使用子程序这个词。
我们可以给一段代码一个名称,然后程序另一部分的一个语句使用这个名称。遇到这个名称时,这个进程的其他部分将会终止,等待这个命名代码被执行。当命名代码执行完毕,将会继续处理下面的语句。命名代码出现的地方被称为调用单元。
子程序有两种形式,一种是只执行特定任务的命名代码,一种是不仅执行任务,还返回给调用单元一个值(值返回子程序)。第一种形式的子程序在调用单元中用作语句,第二种则用作表达式,返回的值被用来评估表达式。
子程序是抽象的一种强力工具。命名的子程序列表允许程序的读者了解到任务已经完成并且不被任务实现的细节所打扰。如果一个子程序需要信息去执行它的任务,便把数据值的名字放在子程序标题的括号中。如果子程序返回一个值给调用单元,它在将要返回的数据名称后面使用单词RETURN。
数的阶乘的定义是这个数与0和它自身之间的所有数的乘积,即
N!=N* (N- 1)!
0的阶乘是1。尺寸系数就是要计算阶乘的数。
基本情况是 Factorial(0)= 1
一般情况是Factorial(N) = N*Factorial(N- 1)
用if语句可以判断N是等于0 (基本情况)还是大于0(一般情况)。显然每次调用N都会减小,所以一定能够达到基本情况。
Write“Enter N”
Read N
Set result to Factorial(N)
Write result +“is the factorialof"+ N
Factorial(N)
IF (N equals 0)
??RETURN 1
ELSE
??RETURN N* Factorial(N- 1)
每次调用Facoral时N都会减小,每次给出的数据称为参数。如果参数足负数会出现什么情况?子程序将不断地调用自身,直到运行时间支持系统耗尽了内存为止。这种情况叫作无限递归,与无限循环等价。
虽然我们在编码二分检索时使用了一个循环,但二分检索算法更像递归。当我们发现了项目或知道了它并不在那里(基本情况)时,便停止检索。我们将继续在它应该出现的数组中寻找该项目(如果它存在)。递归算法必须从非递归算法中调用,正如刚才的阶乘算法那样。
C.A.R.Hoare开发的快速排序算法的基本思想是对两个小列表排序比对一个大列表排序更快更容易。它的名字来源于这种算法通常可以相当快地对数据元素列表进行排序,其基本策略是“分治法”。
这种策略的基础是递归,即每次对一堆试卷排序,都要把它分成两小堆(较小的情况),然后分别对每一小堆试卷应用同样的方法。这过程将持续到不必再分一小堆试卷(基本情况)为止。Quicksort算法的变量first 和last 反映出了当前正在处理的数组data的一部分。
这就提出了非常重要的一点: 永远都不要改造轮子。 算法中的抽象步骤可能已经被你或者其他人解决了。
如果数据是随机排列的,则快速排序是个很好的排序方法。然而,如果数据已经排好序,那么算法退化以保证每个分裂只有一个元素。
递归是一个非常强大和优雅的工具。然而,并不是所有问题都可以很容易地用递归解决,也不是所有问题都有一个明显的递归解决方案从而使问题通过递归解决。即便如此,许多问题的递归解决方案是可取的。如果问题陈述逻辑上分为两种情况(基本情况、一般情况),则递归是一种可行的选择。
我们使用过几次推延细节的思想。曾经用它先给任务命名,而把如何实现任务推延到以后再考虑。在设计过程中,把细节延后具有明显的优势。对于设计的每个特定分层,设计者只考虑与之相关的细节。这种做法叫作信息隐蔽,即在进行高层设计时不能见到低层的细节。
这种做法看来非常奇怪。为什么在设计算法时不能见到细节呢?设计者不是应该无所不
知吗?不是。如果设计者知道一个模块的低层细节,他或她就可能会以这些细节为基础设计这个模块的算法。但是这些低层的细节很可能会发生变化。一旦它们改变了,那么整个模块都要重写。
抽象和信息隐蔽就像一个硬币的两面。信息隐蔽是隐藏细节的做法,抽象则是隐藏细节后的结果。
抽象是复杂系统的一种模型,只包括对观察者来说必需的细节。
控制结构(control structure):用于改变正常的顺序控制流的语句。
抽象 是人们用来处理复杂事务的最强有力的工具
在编写算法时,我们使用速记短语表示要处理的任务和信息,也就是说,给数据和过程一个名字,这些名字叫作标识符。在定义数据值时的标识符来自于单词的组合,使用大写字母来使含义更加清晰。将任务名设为短语,最终会被转换为单独的标示符。
当我们要用一种程序设计语言把算法转换成计算机能够执行的程序时,可能必须修改标识符。每种语言都有自己构成标识符的规则。因此,转换过程分两个阶段,首先在算法中命名数据和动作,然后把这些名字转换成符合计算机语言规则的标识符。请注意,数据和动作的标识符都是抽象的一种形式。
我们已经演示了算法阶段的测试,使用的是算法走查。也展示了如何设计测试方案并用汇编语言实现。测试在编程的每个阶段都十分重要,有两种基本的测试分类:白盒测试,基于代码本身;黑盒测试,基于测试所有可能的输人值。通常来说,一个测试方案包括这两种测试类型。
2019-2020-1学期 20192406 《网络空间安全专业导论》第三周学习总结
标签:怎样 真实机 count 排除 计时器 设置 字符串 方案 整数
原文地址:https://www.cnblogs.com/lj2406/p/11721308.html