标签:视觉 贴图 几何 扫描 工作 协方差矩阵 游戏 img 三维空间
对于一个三维空间的正则曲面R(u, v), 点(u, v)处的切平面(Ru, Rv)的法向量即为曲面在点(u, v)的法向量。点云是曲面的一个点采样,采样曲面的法向量就是点云的法向量。
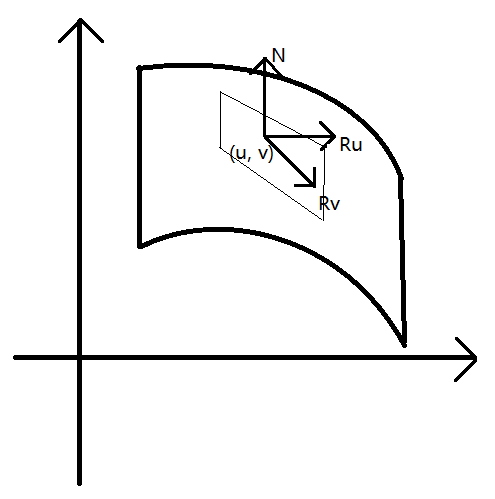
我们给每个点一个线段来显示法线,线段的方向为法线方向,如下图所示。这种显示方法虽然简单,但是不方便查看法线的正确性。下面介绍的点云渲染,能更加直观的查看法线的正确性。
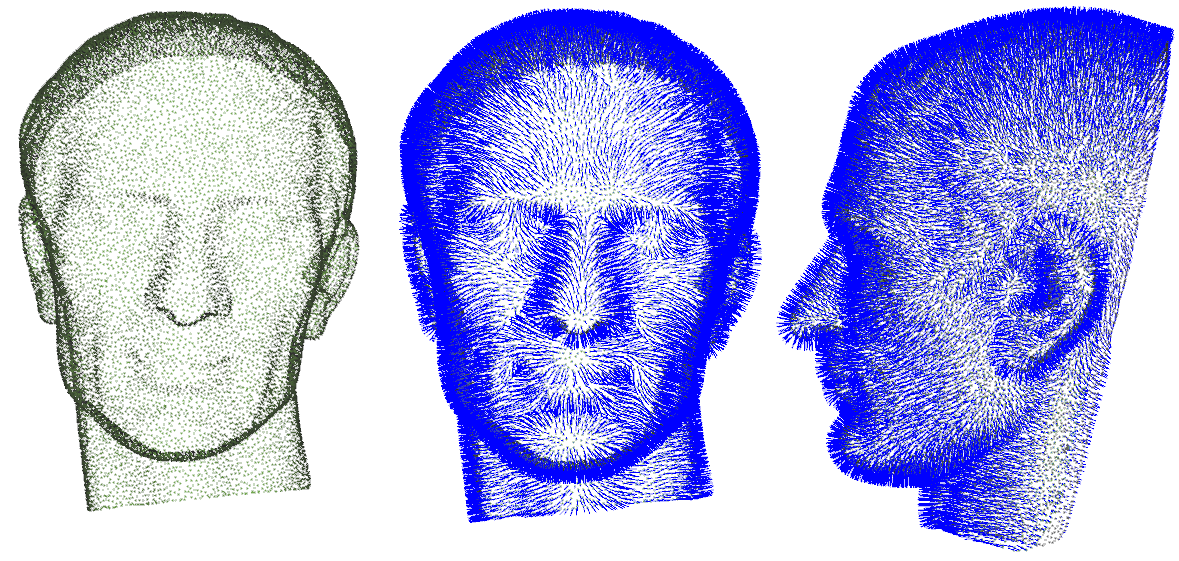

点云渲染也可以用来检查法线的正确性。如下图所示,光源在模型的正前方,左边的渲染图看起来更加符合我们的直观感觉,右图的渲染方式看起来有些不对,是因为法线不准导致的。通过点云的渲染,可以快速定性的检查法线是否正确。至于右图为什么看起来不对,这个就是一个直观感觉,正确的渲染图看多了,就会有感觉了。

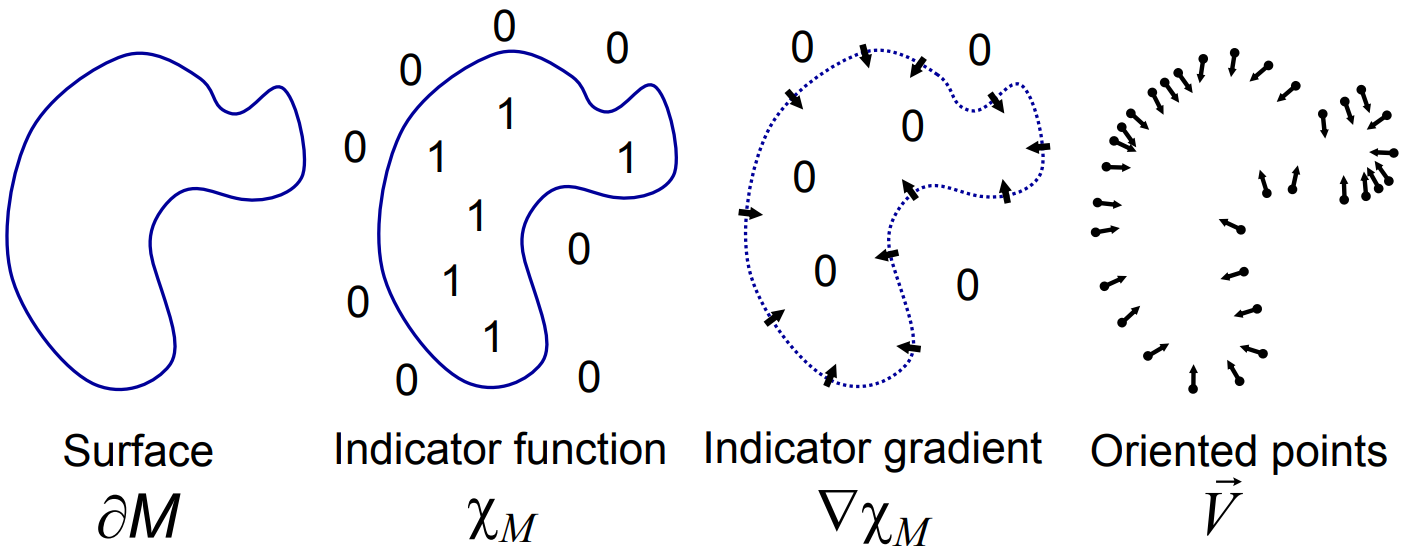


点云采样于物体表面,物体表面的法线即为点云法线,故可先对物体表面的几何进行估计,即可计算出点云法线。一般可用低阶多项式曲面进行局部拟合,如左图所示。如果点云均匀分布,希望计算速度快,也可以用平面进行局部拟合,平面法线即为点云法线,如右图所示。
平面的局部拟合,可以采用PCA(主成分分析)的方法。因为曲面局部是平坦的,法线所在的方向是主成分最低的方向,也就是PCA里面最小特征值对应的特征方向。具体操作如下:1)给每个点计算K邻近邻域(也可以用半径邻域);2)计算PCA的协方差矩阵 Cov = ∑ (Ni – C) X (Ni – C),其中Ni为邻域点,C为中心点。这个协方差矩阵的最小特征值对应的特征向量即为这个点的法线方向。

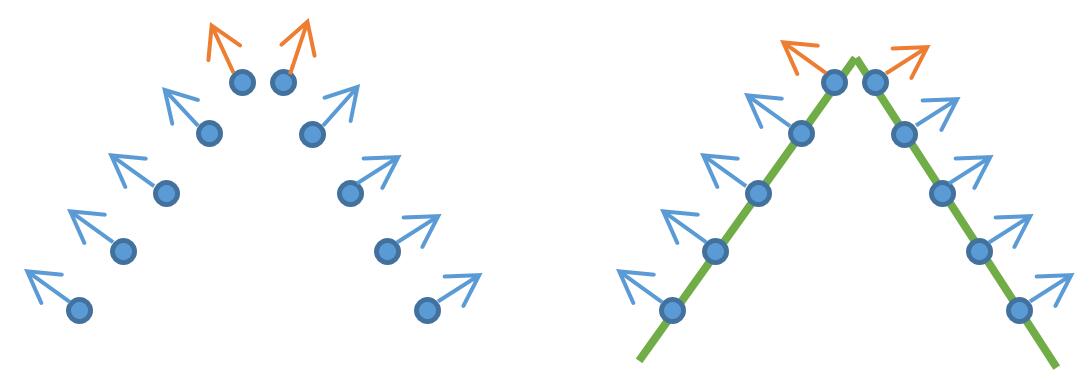
在特征比较尖锐的地方,如左图所示,法线计算容易被光滑掉。右图直线是物体真实的几何,可以比较红色法线方向的差别。特征点的法线,可以用迭代权重的方法来修正,如先用平面局部拟合,然后给局部的点计算权重,离平面越远的点权重越小,然后再用带权重的点局部拟合平面,如此迭代即可。
点云法线经过上面介绍的PCA计算以后,还有一个问题是全局定向。法线有两个互为相反的方向。所谓全局定向,就是视觉上连续的一片点云法线方向要一致,片于片之间的定向也要视觉一致。如下图所示,左图的法线定向是乱的,而右图的法线有一致的定向。对于任给的一个点云,想要完全正确的定向,是不可能的,因为信息的缺失,有些局部上的正确定向是不可能的。但是,也有一些启发式的方法来给点云法线定向,一般情况下是可以正确有效的定向的。

下面介绍一种简单的方法,它是图形学学者Hugues Hoppe在1992年发表的一篇Siggraph论文提到的方法。Hugues Hoppe目前是Google研究院的一名学者,他之前微软研究院工作,毕业于华盛顿大学。早期发表了很多关于曲面重建和网格优化的论文。

如果点云分布比较均匀,在光滑的地方,相邻两个点法线的夹角会很小,可以认为近似平行,即|Ni * Nj| ≈ 1,如果定向一致,则Ni * Nj ≈ 1。一个经典的定向方法是,给点云的每个点找k个最近点,并连上k条边,这样点云就变成一个图结构了,也叫Riemannian图。然后给每条边一个权重w = 1 - |Ni * Nj|。w越小,表明两点之间的法线越接近。然后从某一点出发,找出这个图的最小支撑树(Prim算法和Kruskal算法),并使得相邻点的定向一致。
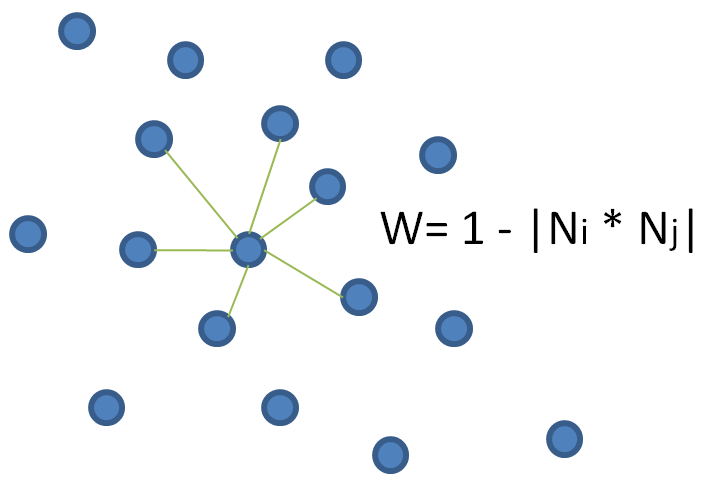
这个定向方法在不光滑的地方,距离很近的薄板等情况下,可能会出问题。另外,如果点云有多个片区,虽然每个片区内部可以定向一致,但是片区之间的整体定向也是很难确定的。有不少论文针对这些情况设计了新的定向方法,但是新方法的条件假设也更多了。从全局效果来讲,不如这个方法的适普性好。因为算法假设越少,适普性也就越好。
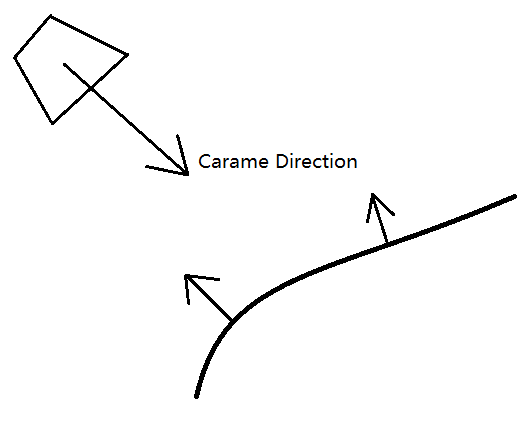
扫描数据是可以完美定向的。因为扫描得到的深度点云,法线与相机方向(Z轴)的夹角小于90度。由于法线有两个互为相反的方向,取与相机方向夹角小于90度的方向(向量点积大于0)。点云做了刚体变换(Matrix4x4::TransformPoint)后,点云法线也要做相应的变换(Matrix4x4::RotateVector,注意坐标点和向量的刚体变换是有区别的)。法线只有在最初的相机坐标系下是可以完美定向的。之后一旦做了刚体变换,想要再去全局定向,就只能采用之前介绍的“法线如何定向”的方法。这些全局定向的方法,都不能做到一定正确,它只能保证每个点云小片的定向一致,片之间的定向一致是没法保证的。
有兴趣的读者,欢迎参考视频版本
标签:视觉 贴图 几何 扫描 工作 协方差矩阵 游戏 img 三维空间
原文地址:https://www.cnblogs.com/threepark/p/11724040.html