标签：传统 级别 生成 输入 text info 输入输出 play dfs
看了看题目，感觉毫无思路，看了看范围，直接上暴搜吧......
一道思路来自数据范围的题......
分析一下数据范围：
那么如果我们要得分，该怎么处理？
一棵树多一条边，必定形成环
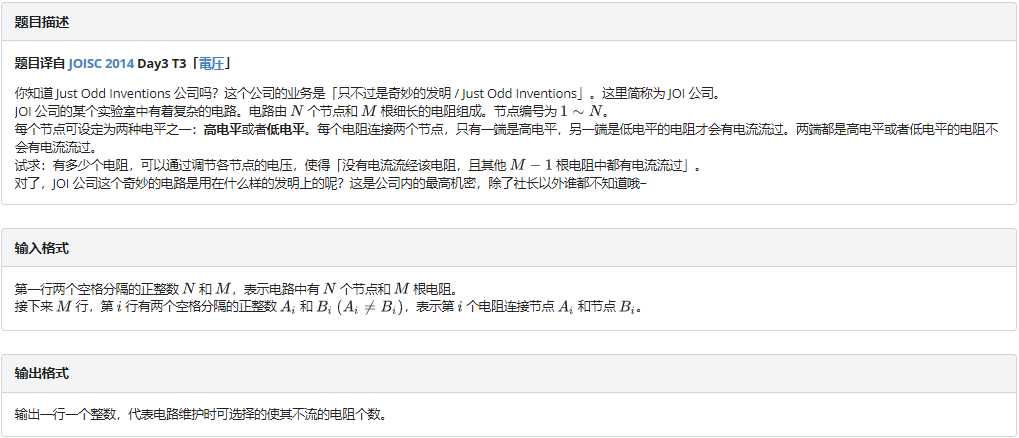
如果这个环是一个奇环，那么我们取的边一定是要在这个环上面，那么答案就是奇环的大小
如果这个环是一个偶环，那么这条边一定不能在这个环上面
嘿，这是不是我们要取的边的限制呢！
我们要取的边，一定要被每一个奇环包含，且不能被任意一个偶环包含
我们再把这道题分析一下，题目没保证必须连通，那么我们把图分开成几个联通块来看。
对于一个联通块，我们模仿 $M=N$ 的思路，先找到这个连通块的某一棵生成树。
首先，我们可以保证，在这个连通块中，不在这个树上的任意一条边，都是连接这个树上的任意两点的
再往后推，如果这条连通块中的边不在树上，那么这条边和生成树的某个部分一定是构成环的。
在此基础上，我们是否可以判断，这个环的奇偶？可以，而且是 $log$ 级别。用 $lca$ 可以很好解决这个问题，细节自行思考。
判断出奇偶后，再利用我们在 $M=N$ 情况下推出的结论：我们要取的边，一定要被每一个奇环包含，且不能被任意一个偶环包含。
按照这种方法，我们只需要把被所有奇环所包含且不被任意一个偶环包含的边选出来，这就是答案了。
但是，树上的边是选到了，那么我们枚举的这条非树边可不可能是答案呢？
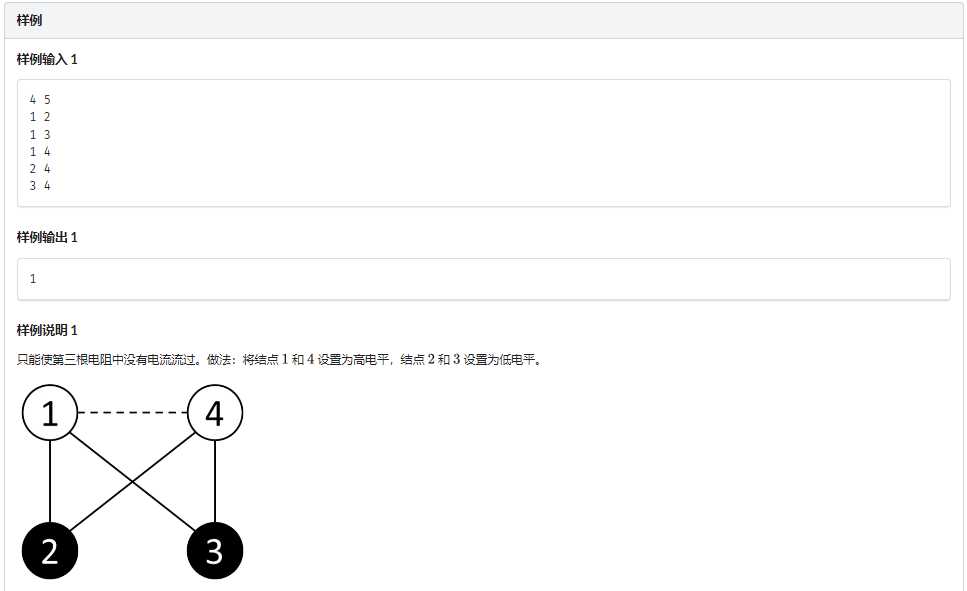
有可能的，但只有一种情况。
首先，在普遍的情况下，这条非树边是不会成为答案边的。为什么？
举个栗子：
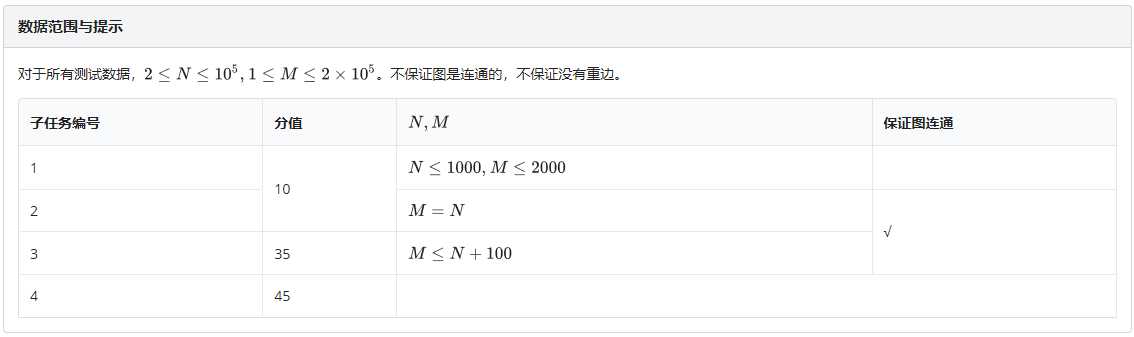
我们先画一棵生成树。
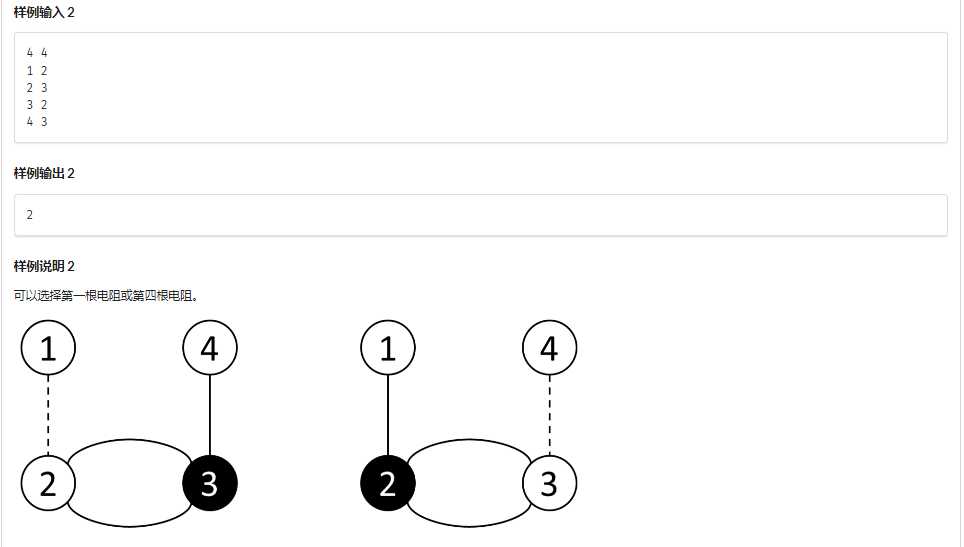
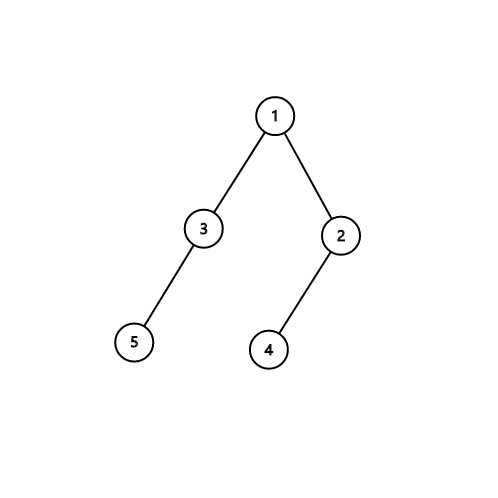
首先，如果一条非树边能成为答案，那么它一定围成一个奇环，那么我们加一条非树边：
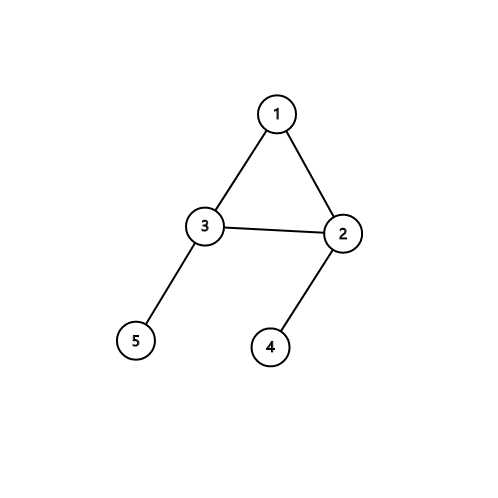
在这样的条件下，$edge_{2,3}$ 是可能成为答案的，但是如果再来一条非树边呢？
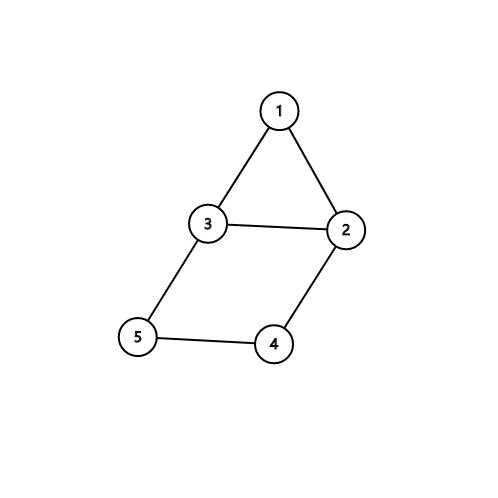可以看出，虽然这里有两个奇环，但是边 $edge_{2,3}$ 与 $edge_{4,5}$ 又围成一个偶环，这又将他们排除了。
从这样一个例子中，再结合一些奇偶分析思想，不难看出，当这个树被围成的奇环只有一个时，非树边是可能成为答案的。
但如果有多个奇环，那么这些非树边都不可能成为答案了。
所以，我们只需要再最后注意一下这个特殊情况即可。
至于最终如何实现，可以使用倍增的思想，如果是偶环，则全部 $-1$ ，否则全部 $+1$ ，将其记录为一条边的得分，最后用一个 $dfs$ 进行下传得分，判断这条边的得分是否等于奇环总个数即可。
这个博客仅有思路......
标签：传统 级别 生成 输入 text info 输入输出 play dfs
原文地址：https://www.cnblogs.com/MachineryCountry/p/11729166.html
