标签:顺序 含义 准备 培养 说明 公约数 基本 mic com
输入2个正整数 \(x0, y0 (2 \le x0 \lt 100000, 2 \le y0 \le 1000000)\) ,求出满足下列条件的 P,Q 的个数。
条件:
试求:满足条件的所有可能的2个正整数的个数。
2个正整数x0,y0
1个数,表示求出满足条件的P,Q的个数
3 604P,Q有4种:
给定一个正整数 \(k(2 \le k \le 15)\) ,把所有k的方幂及所有有限个互不相等的k的方幂之和构成一个递增的序列,例如,当 \(k = 3\) 时,这个序列是:
1,3,4,9,10,12,13,...
(该序列实际上就是: \(3^0,3^1,3^0+3^1,3^0+3^2,3^0+3^1+3^2, \dots\) )
请你求出这个序列的第 \(N\) 项的值(用10进制数表示)。
例如,对于 \(k = 3, N = 100\) ,正确答案应该是981。
2个正整数,用一个空格隔开:
\(kN\) ( \(k\)、\(N\) 的含义与上述的问题描述一致,且 \(2 \le k \le 15 , 10 \le N \le 1000\) )。
1个正整数。(整数前不要有空格和其他符号)。
3 100981NOIP 2006 普及组 第四题
Hanks博士是BT(Bio-Tech,生物技术)领域的知名专家。现在,他正在为一个细胞实验做准备工作:培养细胞样本。
Hanks博士手里现在有 \(N\) 种细胞,编号从 \(1\) 到 \(N\) ,一个第 \(i\) 种细胞经过1秒钟可以分裂为 \(Si\) 个同种细胞( \(Si\) 为正整数 )。现在他需要选取某种细胞的一个放进培养皿,让其自由分裂,进行培养。一段时间以后,再把培养皿中的所有细胞平均分入 \(M\) 个试管,形成 \(M\) 份样本,用于实验。Hanks博士的试管数 \(M\) 很大,普通的计算机的基本数据类型无法存储这样大的 \(M\) 值,但万幸的是, \(M\) 总可以表示为 \(m_1\) 的 \(m_2\) 次方,即 \(M = m_1^{m_2}\) ,其中 \(m_1, m_2\) 居委基本数据类型可以存储的正整数。
注意,整个实验过程中不允许分隔单个细胞,比如某个时刻若培养皿中有4个细胞,
Hanks博士可以把它们分入2个试管,每试管内2个,然后开始实验。
但如果培养皿中有5个细胞,博士就无法将它们均分入2个试管。此时,博士就只能等待一段时间,让细胞们继续分裂,使得其个数可以均分,或是干脆改换另一种细胞培养。
为了能让实验尽早开始,Hanks博士在选定一种细胞开始培养后,总是在得到的细胞“刚好可以平均分入 \(M\) 个试管”时停止细胞培养并开始实验。现在博士希望知道,选择哪种细胞培养,可以使得实验的开始时间最早。
第一行,有一个正整数 \(N\) ,代表细胞种数。
第二行,有两个正整数 \(m_1, m_2\) ,以一个空格隔开,即表示试管的总数 \(M = m_1^{m_2}\) 。
第三行有 \(N\) 个正整数,第 i 个数 \(S_i\) 表示第 i 种细胞经过 1 秒钟可以分裂成同种细胞的个数。
一个整数,表示从开始培养细胞到实验能够开始所经过的最少时间(单位为秒)。
如果无论Hanks博士选择哪种细胞都不能满足要求,则输出整数-1。
1
2 1
3-12
24 1
30 122【输入输出说明】
经过1秒钟,细胞分裂成3个,经过2秒钟,细胞分裂成9个,……,可以看出无论怎么分裂,细胞的个数都是奇数,因此永远不能分入2个试管。
【输入输出样例2说明】
第1种细胞最早在3秒后才能均分入24个试管,而第2种最早在2秒后就可以均分(每试管 \(144/24 = 6\) 个)。故实验最早可以在2秒后开始。
【数据范围】
对于 50% 的数据,有 \(m_1^{m_2} \le 30000\) 。
对于所有的数据,有
\(1 \le N \le 10000, 1 \le m_1 \le 30000, 1 \le m_2 \le 10000, 1 \le S_i \le 2,000,000,000\) 。
NOIP 2009 普及组 第三题
背景
栈是计算机中经典的数据结构,简单的说,栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作,即 pop(从栈顶弹出一个元素)和 push(将一个元素进栈)。
栈的重要性不言自明,任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时,想到了一个书上没有讲过的问题,而他自己无法给出答案,所以需要你的帮忙。
题目描述
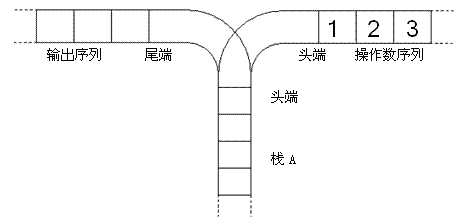
宁宁考虑的是这样一个问题:一个操作数序列,1,2,...,n(图示为1到3的情况),栈A的深度大于n。
现在可以进行两种操作,
将一个数,从操作数序列的头端移到栈的头端(对应数据结构栈的push操作)
将一个数,从栈的头端移到输出序列的尾端(对应数据结构栈的pop操作)
使用这两种操作,由一个操作数序列就可以得到一系列的输出序列,下图所示为由1 2 3生成序列2 3 1的过程。
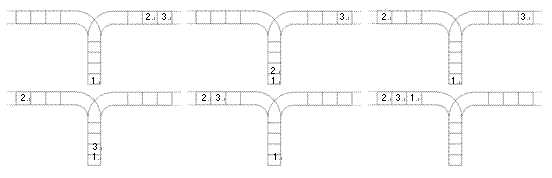
(原始状态如上图所示)
你的程序将对给定的 n ,计算并输出由操作数序列1,2,…经过操作可能得到的输出序列的总数。
输入文件只含一个整数 \(n(1 \le n \le 18)\)
输出文件只有11行,即可能输出序列的总数目。
35给你一个正整数 \(n\) ,请给 \(n\) 分解质因数,并按照样例输出的格式输出对应的结果。
输入包含一个正整数 \(n (1 \le n \le 10^9)\) 。
按照样例输出的格式输出对 \(n\) 分解质因数的结果。注意:质因数需要按照从左往右依次增加的顺序来。
1212=2^2*3600600=2^3*3*5^2标签:顺序 含义 准备 培养 说明 公约数 基本 mic com
原文地址:https://www.cnblogs.com/zifeiynoip/p/11738442.html