标签:方向 eof 正整数 acm NPU www case 相交 using
描述
Now,given the equation 8*x^4 + 7*x^3 + 2*x^2 + 3*x + 6 == Y,can you find its solution between 0 and 100;
Now please try your lucky.
输入
The first line of the input contains an integer T(1<=T<=100) which means the number of test cases. Then T lines follow, each line has a real number Y (fabs(Y) <= 1e10);
输出
For each test case, you should just output one real number(accurate up to 4 decimal places),which is the solution of the equation,or “No solution!”,if there is no solution for the equation between 0 and 100.
样例输入
2
100
-4
样例输出
1.6152
No solution!
#include<bits/stdc++.h> using namespace std; double f(double x) { return 8*x*x*x*x+7*x*x*x+2*x*x+3*x+6; } double erfen(double y,double l,double r) { while(r-l>1e-8) { double mid=(l+r)/2; if(f(mid)>y) r=mid; else l=mid; } return r; } int main() { int n; double y; cin>>n; while(n--) { cin>>y; if(f(0)>y+1e-3||f(100)<y-1e+3) cout<<"No solution!"<<endl; else printf("%0.4f\n",erfen(y,0,100)); } }
描述
对于给定的一个长度为N的正整数数列A[i],现要将其分成M(M≤N)段,并要求每段连续,且每段和的最大值最小。
关于最大值最小:
例如一数列4 2 4 5 1要分成3段
将其如下分段:
[4 2][4 5][1]
第一段和为6,第2段和为9,第3段和为1,和最大值为9。
将其如下分段:
[4][2 4][5 1]
第一段和为4,第2段和为6,第3段和为6,和最大值为6。
并且无论如何分段,最大值不会小于6。
所以可以得到要将数列4 2 4 5 1要分成3段,每段和的最大值最小为6。
输入
第1行包含两个正整数N,M,第2行包含N个空格隔开的非负整数A[i],含义如题目所述。
M<=N<=100000, A[i]之和不超过109
输出
仅包含一个正整数,即每段和最大值最小为多少。
样例输入
5 3
4 2 4 5 1
样例输出
6
#include<bits/stdc++.h> using namespace std; int a[100005]; int n,m,sum; int panduan(int zhi) { int sum1=0,num=1; for(int i=1;i<=n;i++) { if(a[i]>zhi) return n; if(sum1+a[i]<=zhi) sum1+=a[i]; else { sum1=a[i]; num++; } } return num; } int main() { cin>>n>>m; for(int i=1;i<=n;i++) { cin>>a[i]; sum+=a[i]; } int l=0,r=sum; while(l<r) { int mid=l+r>>1; int x=panduan(mid); if(x>m) l=mid+1; else r=mid; } cout<<l<<endl; }
描述
一个点每过一个单位时间就会向四个方向扩散一个距离,如图。
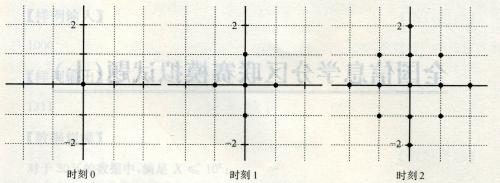
两个点a、b连通,记作e(a,b),当且仅当a、b的扩散区域有公共部分。连通块的定义是块内的任意两个点u、v都必定存在路径e(u,a0),e(a0,a1),…,e(ak,v)。给定平面上的n给点,问最早什么时刻它们形成一个连通块。
输入
第一行一个数n,以下n行,每行一个点坐标。
对于20%的数据,满足1≤N≤5;1≤X[i],Y[i]≤50;
对于100%的数据,满足1≤N≤50;1≤X[i],Y[i]≤109。
输出
一个数,表示最早的时刻所有点形成连通块。
样例输入
2
0 0
5 5
样例输出
5
对时间进行二分最长的时间是1e9判断时候联通只要dfs一遍最后看有没有遍历所有点就可以了
#include<bits/stdc++.h> using namespace std; int x[100],y[100],n,mid; bool vis[100]; void dfs(int s) { vis[s]=1; for (int i=1;i<=n;i++) if (!vis[i]&&abs(x[i]-x[s])+abs(y[i]-y[s])<=mid*2) dfs(i); } int liantong() { memset(vis,0,sizeof(vis)); dfs(1); for (int i=1;i<=n;i++) if (!vis[i]) return 0; return 1; } int main() { std::ios::sync_with_stdio(false); scanf("%d",&n); for (int i=1;i<=n;i++) scanf("%d%d",&x[i],&y[i]); int64_t l=0,r=2e9; while (l<r) { mid=(l+r)/2; if (liantong()) r=mid; else l=mid+1; } cout<<l<<endl; }
描述
我们都知道一场比赛总共有10道题,所以这是最后一道。
为什么最后一道是第9道?因为作为一名码农,我们要学会从0开始编号。
那么这又跟这道题有什么关系呢?其实没有关系……
事情是这样的,小白最近发大财了,买了一大箩筐萝卜,总共有N个,然后他把这些萝卜按照一行放在桌子上。
每个萝卜大小不同,所以价值也不同。
现在小白打算把这些萝卜分给大家――但是刚好不给你。
很幸运的是,你得到了分萝卜的权力――虽然你分不到。
小白让你把这些萝卜分成最多M段,然后他们那些人每人选一段拿走,如果他们的人数不够M,那么剩下的萝卜就会被扔掉。
小白这种宁愿把萝卜扔掉都不给你的行为让你恨得牙痒痒,所以你决定让最多的那一段的价值之和尽可能的小,这样他们每个人都不会爽到。
输入
输入的第一行是样例数T,1 ≤ T ≤ 20。
每组样例占一行,包含两个整数N、M,表示小白买了N个萝卜,让你分成M段,1 ≤ N ≤ 100,000,1 ≤ M ≤ N;
接下来一行有N个整数,分别是萝卜们的价值,1 ≤ 萝卜的价值 ≤ 100。
输出
每组样例输出一行,包含一个整数X,是价值之和最大的那一段的价值之和。
样例输入
1
5 3
1 5 4 2 3
样例输出
6
#include<bits/stdc++.h> using namespace std; int a[100005]; int n,m,sum; int panduan(int zhi) { int sum1=0,num=1; for(int i=1;i<=n;i++) { if(a[i]>zhi) return n; if(sum1+a[i]<=zhi) sum1+=a[i]; else { sum1=a[i]; num++; } } return num; } int main() { std::ios::sync_with_stdio(false); int t; cin>>t; while(t--) { cin>>n>>m; sum=0; for(int i=1;i<=n;i++) { cin>>a[i]; sum+=a[i]; } int l=0,r=sum; while(l<r) { int mid=l+r>>1; int x=panduan(mid); if(x>m) l=mid+1; else r=mid; } cout<<l<<endl; } }
描述
最近桃子爱上了博彩,一天他买了一张彩票,上面印着带有n个数字的序列a1a2a3...an。
如果一张彩票是幸运的,当且仅当其满足如下全部条件:
1. 序列能被恰好分成不相交的至少2段;
2. 每一段区间[l,r]的和都是相同的。
请你帮助桃子判断他手上的彩票是不是幸运的。
例如123426是幸运的,它可以分为3段,123、42和6,1+2+3=4+2=6。
不相交就是序列的每个数字恰好属于一个段。
输入
第一行一个整数T(≤100),代表有T组数据。
对于每组数据,第一行一个整数n(2≤n≤100),代表彩票中数字序列的位数。
第二行为一个长度为n的数字序列a1a2a3...an(0≤ai≤9)。
输出
如果这张彩票是幸运的,输出YES,否则输出NO。
样例输入
2
5
73452
4
1248
样例输出
YES
NO
提示
第一个样例:能分成3段,7、34和52,7=3+4=5+2。
第二个样例:不能分出。
这个题不知道怎么二分,就直接从前往后了。避免一下后置的0就行。
#include<bits/stdc++.h> using namespace std; string s; int a[101],n,sum; int panduan(int y) { int sum=a[y]; int x=0; for(int i=y+1;i<n;i++) { if(x+(s[i]-‘0‘)<sum) { x+=s[i]-‘0‘; } else if(x+(s[i]-‘0‘)==sum) { x=0; } else return 0; } if(x!=sum&&x!=0) return 0; return 1; } int main() { int t; cin>>t; while(t--) { int f=0; cin>>n; sum=0; cin>>s; for(int i=0;i<n;i++) { sum+=s[i]-‘0‘; a[i]=sum; } int moduan=n-1; for(int i=n-1;i>=0;i--) { if(s[i]==‘0‘) moduan--; else break; } if(moduan==-1) cout<<"YES"<<endl; else { for(int i=0;i<moduan;i++) { int flag=panduan(i); if(flag) { cout<<"YES"<<endl; f=1; break; } } if(f==0) cout<<"NO"<<endl; } } }
标签:方向 eof 正整数 acm NPU www case 相交 using
原文地址:https://www.cnblogs.com/xbqdsjh/p/11739130.html