标签：就会 观察 迭代 偏差 数据 http 十分 UNC 计算
马上要修考出愿了
需要给导师再submit一份研究计划书，
根据之前导师的期望，硕士阶段的学习主要针对GAN在蛋白质设计方面的应用
所以在复习数学和专业课的百忙之中啊，必须再肝一份新的研究计划书出来，
首先从经典的GAN入手，再学习一下WGAN，然后就开始考虑自己在这方面的想法。
GAN
GAN主要由两个部分组成，一个Generator，一个Discriminator。
Generator的输入是一个随机的采样数据或者是一个噪声，将Generator通过真实数据进行训练，使其输出的是我们想要生成的目标。
Discriminator是一个分类器，对于真实的目标返回1，对于生成的虚假目标返回0。
Generator要生成能够迷惑Discriminator的目标，而Discriminator要尽可能辨别出虚假的生成目标，
两个model相当于在不停的对抗，通过Discriminator和Generator的互相对抗迭代并进化，最后Generator
将能够生成足够以假乱真的目标。
1.GAN的原理
首先，对于任何一个真实的数据集，我们可以知道真实目标的分布Pdata(x)，x 是一个真实数据，例如，我们可以把真实的数据想象成一个向量，
这个向量的分布就是Pdata(x)。Generator的目标就是要生成一系列服从这个分布的新的向量，假设我们现在已有的Generator所能生成的分布是PG(x|θ)，
θ是控制这个分布的一系列参数，我们的目标就是要通过训练θ来使得Generator能够尽可能使得生成的artifacts符合真实的数据分布Pdata(x)。
所以对于Generator的训练，我们首先收集一系列真实的数据D={x1, x2, ... , xm}，则对于参数θ和某一个真实数据xi，Generator生成的数据xi的联合概率密度函数为PG(xi |θ)，
则我们可以通过{x1, x2, ... , xm}计算一个似然，即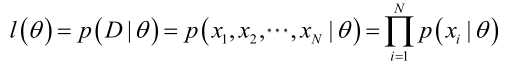
通过得到使这个似然函数最大时θ的值来训练Generator：
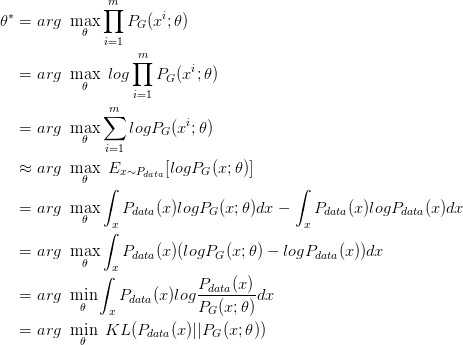
通过以上的一系列推导，我们可以看到结果，Generator生成的数据最接近真实分布时能够使这个似然函数达到最大值。即尽可能地让Generator生成真实的数据。于是我们应该寻找一个θ*来使得PG更接近Pdata。我们假设PG(x|θ)是一个NN，那么随机产生一个向量z，通过G(z)=x这个网络，生成数据x。如何比较G()生成数据的分布是否与真实分布相同呢？取一组Z作为sample，这组Z符合一个分布，通过G()后就可以生成另一个分布PG，用这个PG来与真实分布Pdata进行比较。
众所周知，NN只要有非线性激活函数就可以去拟合任意的函数，那么分布也是可以通过正态分布，高斯分布等分布进行取样，去通过深度学习学习到一个很复杂的分布。
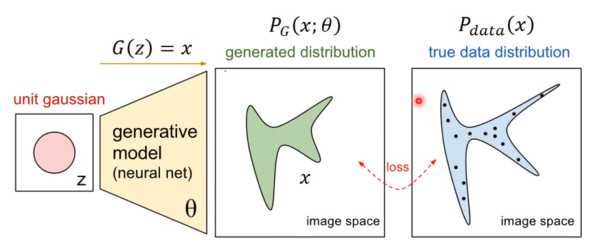
通过generative model得到一个generated distribution，也就是得到artifacts的分布，这个分布与真实数据的分布是很相似的。GAN的作用就是发掘通过改变参数θ来找到这个十分接近真实的分布。GAN的公式如下：
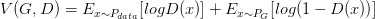（G=Generator，D=Discriminator）
我们的目的是要找到一个足以生成以假乱真的数据分布的Generator G*，同时，对于给定的每一个版本的G，D需要尽可能得找到G产生的数据与真实数据得不同，
于是对于每一代G就会有最优Discriminator D*=
，然后纵观整个G和D的进化过程，可以找到一个最优的
。
现在我们固定G，求解一个最优的D，于是V(G,D)展开后写成以下形式：
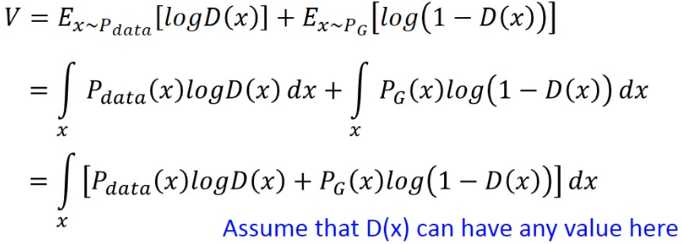
在这里，先假设D(x)可以取任何值，那么脱去积分号，相当于我们要求以下这个函数的最大值
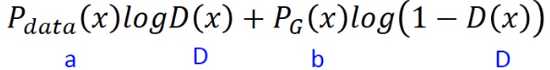
对原式进行换元，可得一个关于D的函数：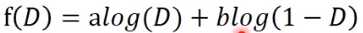
；对D进行求导，可得该函数取最值时的D：
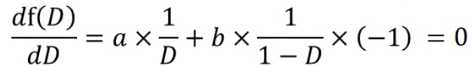
即：
，所以对于一个给定的G，得到最优的D*就是这个。把D*代入得
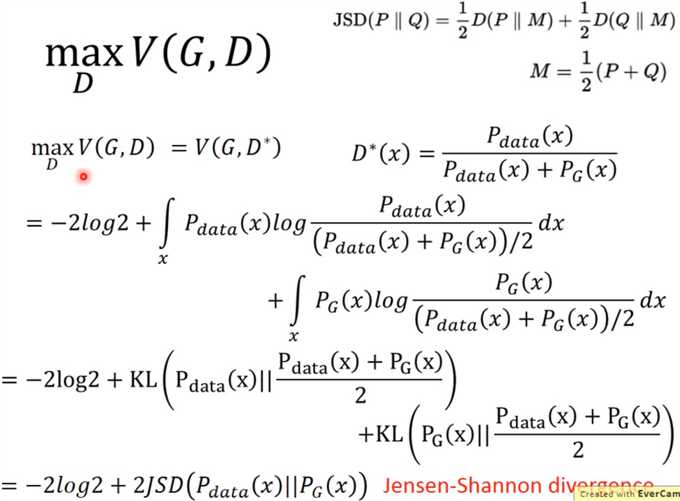
其中最后出现了一种新的divergence，叫做Jensen-Shannon divergence，也是用来衡量两种不同的分布之间的差异的，如果两个分布完全无关(没有交集)，
那么JSD的值是log2，如果两个分布的值完全一样，那么JSD=0.弄整齐一点，给定一个G，有
那么当
时，G=G*.
同时，为了得到G*和D*我们需要找到Loss Function以方便我们通过Gradient Descent来找到G*和D*
GAN的训练过程及Generator和Discriminator的loss function如下图：
其中，得到D*可能需要多次Gradient Descent才能到达max点，而对于G，如果更新后的Gnew比之前的Gold有V(Gold,Dold)<V(Gnew,Dnew),
避免这种情况的办法就是每次少更新一点G，于是就有了上图所示的，D更新多次，而G只更新一次，并且，我们无法保证Gradient Descent之后的点是全局最值点，
只能确定它是局部最值点。
2.经典GAN存在的问题
log(1-D(x))是G在训练时的loss function，但是通过观察函数图像，可以发现，D(x)在接近于0的时候，函数的梯度很小，这样会导致在刚开始时G的收敛变得十分缓慢，我们可以改变这个loss function，将其修改为
，这样这个loss function的趋势就变成了上面的那条曲线，趋势不变，但函数在刚开始训练时梯度很大，而在最后快收敛时梯度很小，这与我们训练时的想法是相吻合的。
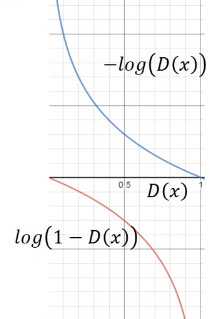
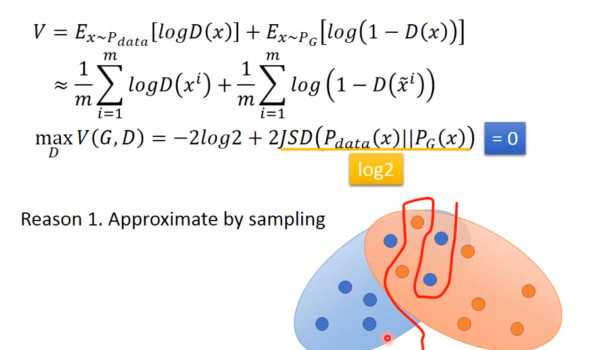
另一个问题：因为我们在GAN的训练中使用的是两个分布的Sampling，所以我们在对D进行训练时会发现，无论我们有如何powerful的G，因为数据来源于采样，所以PG 和 Pdata 完全没有交集，以至于我们的Discriminator总是能分辨出那些artifacts，如下图所示，Discriminator总能找出分辨PG 和 Pdata的方法：
这时我们就想到是否能让Discriminator更弱一点，但又想让它能够区分出假图片，所以就产生了矛盾。还有一种可能，假设两个分布都是很窄的（例如线），那么JSD=log2，也就相当于没有交集，这样子无法对Generator进行Gradient Descent，有一种解决办法就是添加噪声，让两个分布变得很宽，这样就可以计算出JSD，但随着时间变化，需要减小噪声，使得两个分布趋同。
还有一个问题，叫做Mode Collapse，这个是因为Generator在很多情况下无法生成具有多样性的分布（例如生成多个高斯分布），这就与我们想象中的训练过程产生了偏差，我们希望Generator能够生成尽可能和真实分布一样的分布，但是Generator往往只能够生成真实分布的其中一种情况，比如说我们用猫狗牛羊这几种动物的图片去训练一个GAN，希望它也能够生成这几种动物的图片，但是GAN最后得出的结果是只能够生成狗的图片。
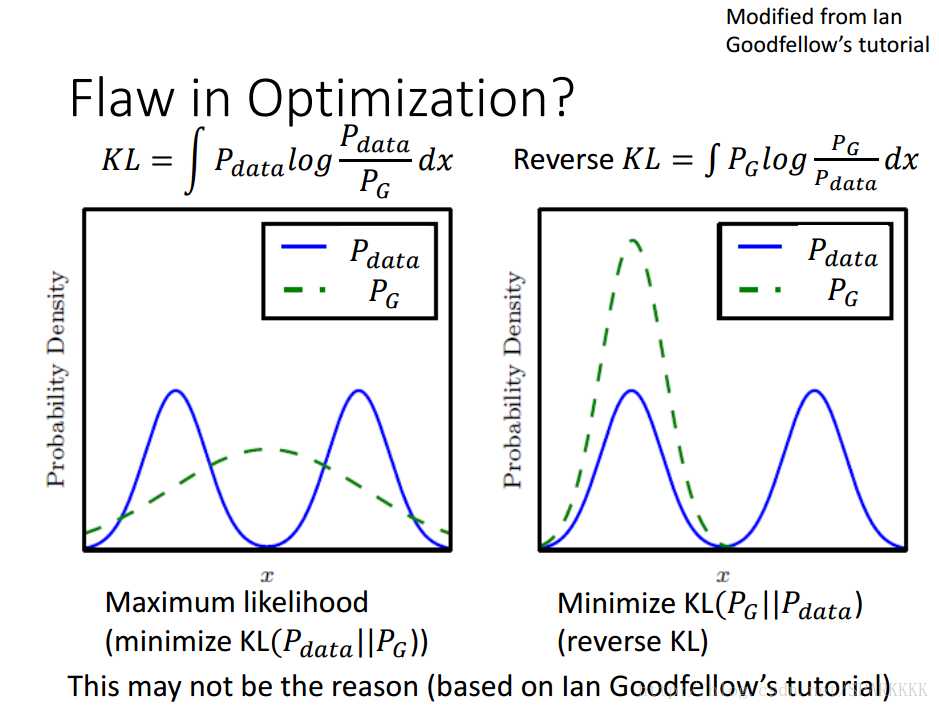
对于左边的分布，当Pdata有值而PG没有取值时，KLD会趋向于无穷大，因此为了不让KLD趋向无穷大Generator要在每个有Pdata的地方都有一个PG，而鉴于它本身的特性，它无法生成多个高斯分布，所以只能够尽可能地去覆盖Pdata的分布曲线，所以就造成了左图的情形。这样虽然不是Mode Collapse，但是会产生许多无意义的样本，训练结果效果很差。
对于右边的分布，当PG有值时，Pdata也一定要有取值，否则Generator将面临一个非常大的惩罚，因此为了避免惩罚，Generator趋向于在确定正确的分布内生成数据，而不去尝试在别的分布内产生不一样的数据，这样就造成了Mode Collapse，我们的Generator对于一个多个高斯分布叠加的真实分布，只会去产生其中一个高斯分布的数据。
3.对于经典GAN的总结
终于把GAN给看完了，说说我自己的感想，确实是个很不错的思想，但是仔细一想，有非常多的缺点，直接把经典的GAN拿来解决现实问题很可能不会有很好的效果。具体来说，经典GAN大概有以下缺点：
（1）训练困难（2）生成器和判别器的loss无法指示训练进程（3）生成样本缺乏多样性等
对于经典的GAN的这些缺点，有各种论文提出了各种改进，比较著名的有通过Wasserstein距离进行改进的WGAN，解决了GAN训练不稳定，基本解决了mode collapse问题，并且有一个类似于交叉熵的量来表示训练的进程和结果的好坏，这个量越小代表生成的样本质量越好。
近来还有把强化学习与GAN进行结合的seq-GAN，我自己的初步想法也是探索一下seq-GAN在蛋白质设计方面有没有什么用武之地，第一部分先写这些内容吧，下一步学习一下WGAN和seq-GAN然后看看有没有已经做出一些成果的大佬，来探求一下将seq-GAN运用在蛋白质设计方面的可能性。
标签：就会 观察 迭代 偏差 数据 http 十分 UNC 计算
原文地址：https://www.cnblogs.com/MemoryOfStars/p/11755693.html
