标签:mic 运行 inux 数值 linux alt bsp pac 命令
内容:
IMU原理与模型
后端优化与VIO BA
滑动窗口算法与FEJ
后端求解系统与代码
前端介绍
VIO初始化
VIO系统回顾
预备知识:
数学:线性代数、微积分、概率论
编程:Linux、C++、OpenCV
英语:文献阅读
专业知识:2D/3D 计算机视觉、图像处理
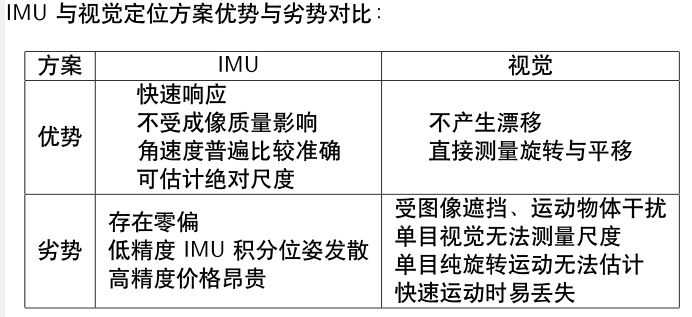
以视觉与IMU融合实现的里程计
IMU:惯性测量单元
组成:陀螺仪和加速度计,共6轴。
较高频率(>100Hz),易受自身温度、零偏、振动等因素干扰,积分得到的平移与旋转容易漂移。
视觉:
较低频率(15-60Hz居多),通过相机特整点进行匹配,推断相机运动。
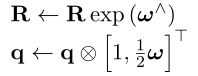
以上2种导数更新方式,误差相差不大。证明代码如下:
1 #include <iostream> 2 #include <cmath> 3 using namespace std; 4 5 #include <Eigen/Core> 6 #include <Eigen/Geometry> 7 8 #include "sophus/so3.h" 9 #include "sophus/se3.h" 10 11 int main( int argc, char** argv ) 12 { 13 // 沿Z轴转90度的旋转矩阵 14 Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix(); 15 16 17 // 四元数乘法饶动微元 18 Eigen::Matrix<double,4,1> w_q ; 19 20 w_q << 0.005,0.01,0.015,1; 21 22 23 // 李树饶动微元 24 Eigen::Vector3d w; 25 26 w << 0.01,0.02,0.03; 27 28 29 // 生成李树与四元数 30 Sophus::SO3 SO3_R(R); // Sophus::SO(3)可以直接 31 Eigen::Quaterniond q(R); // 或者四元数 32 33 cout<<"\n***********准备开始*******************\n"<<endl; 34 35 cout<<endl; 36 cout<<"R : \n"<<R<<endl; 37 38 cout<<"******************************"<<endl; 39 40 cout<<endl; 41 cout<<"SO(3) from matrix: \n"<<SO3_R<<endl; 42 43 cout<<endl; 44 cout<<"q : \n"<<q.coeffs()<<endl; 45 46 cout<<"************我是分割线*****************\n\n\n"<<endl; 47 48 // 计算饶动后的数值 49 Sophus::SO3 SO3_updated_R_left = Sophus::SO3::exp(w)*SO3_R; 50 Sophus::SO3 SO3_updated_R_right = SO3_R*Sophus::SO3::exp(w); 51 52 53 cout<<"***********R饶动的值(李树)**********"<<endl; 54 cout<<"**********R饶动的值(左)*********"<<endl; 55 56 cout<<"SO3 updated = \n"<<SO3_updated_R_left<<endl; 57 58 cout<<"**********R饶动的值(右)*********"<<endl; 59 60 cout<<"SO3 updated = \n"<<SO3_updated_R_right<<endl; 61 62 cout<<"***************************************\n\n\n"<<endl; 63 64 /********************萌萌的分割线*****************************/ 65 cout<<"************我是分割线*****************"<<endl; 66 67 //计算四元数的值 68 Eigen::Quaterniond w_q_0(w_q); 69 Eigen::Quaterniond q_updated_left; 70 Eigen::Quaterniond q_updated_right; 71 72 q_updated_left = w_q_0 * q; 73 q_updated_right = q * w_q_0; 74 75 q_updated_left.normalize(); 76 q_updated_right.normalize(); 77 78 cout<<"***********四元数饶动的值*********\n"<<endl; 79 cout<<"***四元数饶动的值(微变量)*******"<<endl; 80 81 cout<<"w_q = \n"<<w_q_0.coeffs()<<endl; 82 83 cout<<"\n***四元数饶动的值(结果zuo)******"<<endl; 84 85 cout<<"q_updated = \n"<<q_updated_left.coeffs() <<endl; 86 87 cout<<"***四元数饶动的值(结果you)*********"<<endl; 88 89 cout<<"q_updated = \n"<<q_updated_right.coeffs()<<endl; 90 91 cout<<"***************************************\n\n\n"<<endl; 92 93 //传结果 94 cout<<"************我是分割线*****************"<<endl; 95 96 cout<<"***********jie guo*********\n"<<endl; 97 98 cout<<"***************************************"<<endl; 99 100 cout<<"李树上(左) = \n"<<SO3_updated_R_left<<endl; 101 102 cout<<"***************************************"<<endl; 103 104 cout<<"李树上(右) = \n"<<SO3_updated_R_right<<endl; 105 106 107 Sophus::SO3 SO3_q_l(q_updated_left ); 108 Sophus::SO3 SO3_q_r(q_updated_right); 109 110 111 cout<<"\n***四元数饶动的值(结果zuo)******"<<endl; 112 113 cout<<"q_左 = \n"<<SO3_q_l<<endl; 114 115 cout<<"***四元数饶动的值(结果you)*********"<<endl; 116 117 cout<<"q_右 = \n"<<SO3_q_r<<endl; 118 119 cout<<"***************************************\n\n\n"<<endl; 120 121 122 return 0; 123 }
并请在CMakeList.txt添加,下面代码:
cmake_minimum_required( VERSION 2.8 ) project( useSophus ) # 为使用 sophus,您需要使用find_package命令找到它 find_package( Sophus REQUIRED ) include_directories( ${Sophus_INCLUDE_DIRS} ) add_executable( useSophus useSophus.cpp ) target_link_libraries( useSophus ${Sophus_LIBRARIES} )
以上是在cmake下,进行运行。具体自行查看cmake操作,后续会上传至,GitHub上。或,自行学习。
运行结果:

以上仅是学习之用。GitHub 地址:https://github.com/icra205
标签:mic 运行 inux 数值 linux alt bsp pac 命令
原文地址:https://www.cnblogs.com/0201x/p/11768231.html