标签:考试总结 限制 through 情况 gcd 结果 == sum 出现
考试心得:
T1考场上找规律,想了好久的整除分块,无果,心态十分爆炸,无奈之下出去转了一圈。
回来之后突然就想着把最初的想法延续下去,然后似乎找到了一些规律
拼命打表伪证xjb尝试什么的,可算是挂上了对拍
然后T2的贪心也很迷,根本就没想到这是原题
T3一看就是神题最后留着时间也不太够了
T1
第一眼就是要拆开向下取整
先写我考场上的推法:
不考虑取整的结果是(1+p)*q/2
需要减的是取整少的东西
取整一般跟取余相关,所以我们先求\sum {i*q%p}
然后就打表,令d=gcd(p,q)
发现是循环的 len=p/d ,次数times= d
每一节的s1=gcd* \sum{1~(p/d-1)}
所以:\sum {i*q%p}=s1*gcd然后就十分混乱的试出了一个系数1/p
其实可以这么搞 a%b==a-floor(a/b)*b
移项:floor(a/b)==a/b -(a%b)/b
然后就用上了上面所求了
正解是:
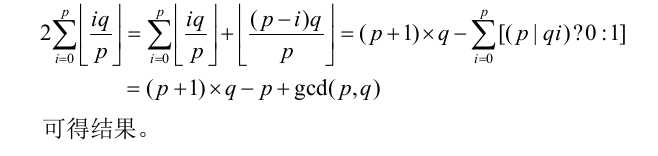
那个gcd怎么来的?
即证明p-gcd(p,q)==\sum i\in [1,p]那一坨。。。
即证 p | i*q 的个数是gcd个
另pp=p/d,qq=p/d
pp| i*qq 成立,当且仅当 i | pp, 而此时i在 [1,p]内只有d个
T2「贪心」
后一种情况与X国军队相同
首先一个贪心是先收益正的,再进行亏损
现在把所有情况变成:打怪。打前需要a点血,打后成了b点血
对于 a<b 即收益为正的情况:我们让a从小到大排序
初始血条为0。。。每打一个怪就会有收益,i
最终所有收益是相同的,每次就让需要的限制尽量小
那可能你会问,我直接打最肥的收益最大的不就行了?
但显然你还要达到一个a的限制,你能打这个了,那为什么不先把a-1,a-2的都干掉多收益一些 呢?
对于a>b 即出现亏损的情况:我们让b从大到小排序处理
每打一个怪就会有亏损
我们打完所有怪减少的血量总和是一定的,而我每次只希望尽量少的用血瓶
所以就每次就多剩点
Miemeng:引用某电池广告:××用完了,***还能接着用。。。。。
要是你先打b最小的,然后你就要补更多的血,最后剩了一个b次小的,然后你发现你多补的那些血没用了
似乎证明掺杂了各种思路十分混乱
标签:考试总结 限制 through 情况 gcd 结果 == sum 出现
原文地址:https://www.cnblogs.com/casun547/p/11771845.html