标签:建模 比较 受限 tps count 多少 over 包含 size
论文链接:https://arxiv.org/pdf/1803.01271.pdf
TCN特点:
TCN组成:
\[TCN = 1D \ FCN + causal convolutions\]
TCN结构图:
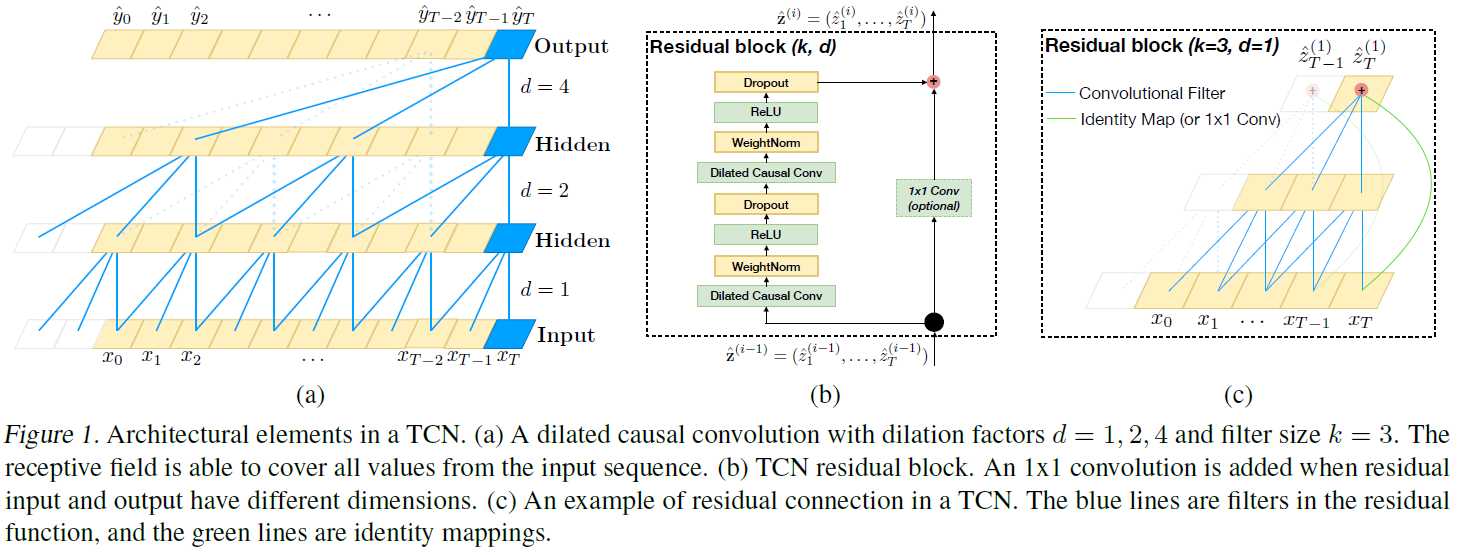
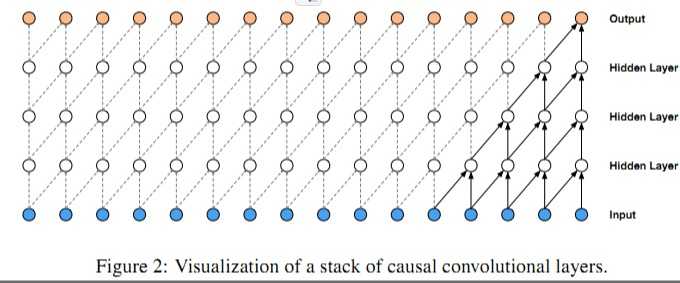
因果卷积可以用上图直观表示。 即对于上一层t时刻的值,只依赖于下一层t时刻及其之前的值。和传统的卷积神经网络的不同之处在于,因果卷积不能看到未来的数据,它是单向的结构,不是双向的。也就是说只有有了前面的因才有后面的果,是一种严格的时间约束模型,因此被成为因果卷积。
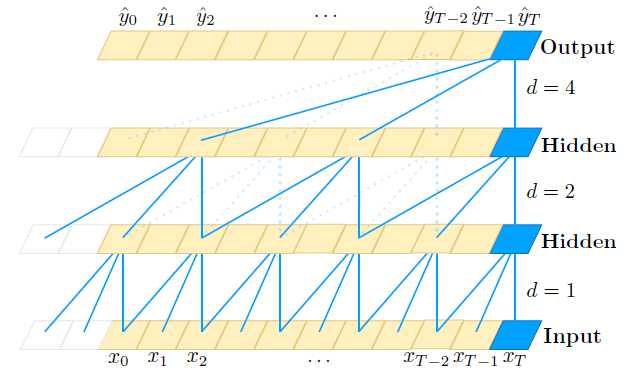
如图TCN结构图(a)。单纯的因果卷积还是存在传统卷积神经网络的问题,即对时间的建模长度受限于卷积核大小的,如果要想抓去更长的依赖关系,就需要线性的堆叠很多的层。为了解决这个问题,研究人员提出了膨胀卷积。
膨胀卷积(dilated convolution)是通过跳过部分输入来使filter可以应用于大于filter本身长度的区域。等同于通过增加零来从原始filter中生成更大的filter。
The dilated convolution operation F on element s of the sequence is defined as: \[F(s)=(x*_df)(s)=\overset{k-1}{\underset{i=0}\sum}f(i) \cdot x_{s-d \cdot i}\]
where d is the dilation factor, k is the filter size, and \(s-d\cdot i\) accounts for the direction of the past.
越到上层,卷积窗口越大,而卷积窗口中的“空孔”越多。d是扩展系数(即评价“空孔”的多少)。
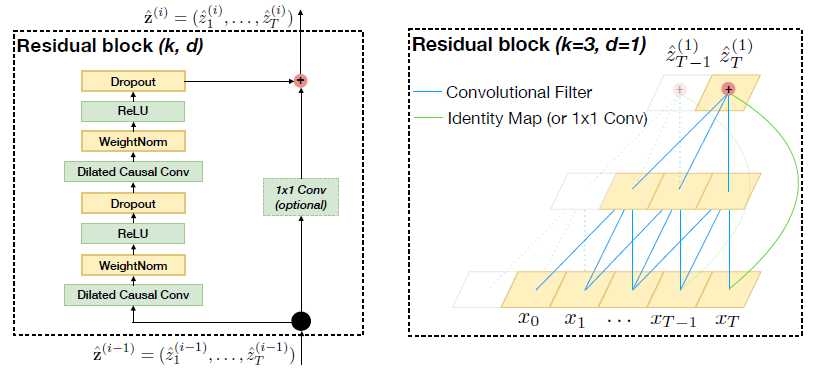
如图TCN结构图(b)。 残差链接被证明是训练深层网络的有效方法,它使得网络可以以跨层的方式传递信息。本文构建了一个残差块来代替一层的卷积。如上图所示,一个残差块包含两层的卷积和非线性映射,在每层中还加入了WeightNorm和Dropout来正则化网络。为什么要1×1卷积呢?1×1卷积是可以用来降维的 。作者直接把较下层的特征图跳层连接到上层,对应的每个Cell的特征图数量(也就是通道数channel)不一致,导致不能直接做类似Resnet的跳层特征图加和操作,于是,为了两个层加和时特征图数量吻合,用1×1卷积做了一个降维的操作。
引用:
标签:建模 比较 受限 tps count 多少 over 包含 size
原文地址:https://www.cnblogs.com/xym4869/p/11777256.html