二维MLE线段树

标签：info   放大   tmp   idt   width   行操作   tag   nbsp   代码   

关于二维线段树，ta死了

先来看看两种二维线段树的打法

1.四叉树

 然而ta死了，ta是$\Theta (n)$的,加上线段树的常数,$T$飞稳

2.线段树套线段树

我尽量画出来...

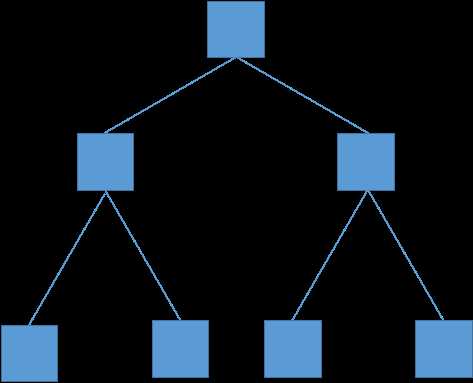
 图中每个方块是一棵线段树

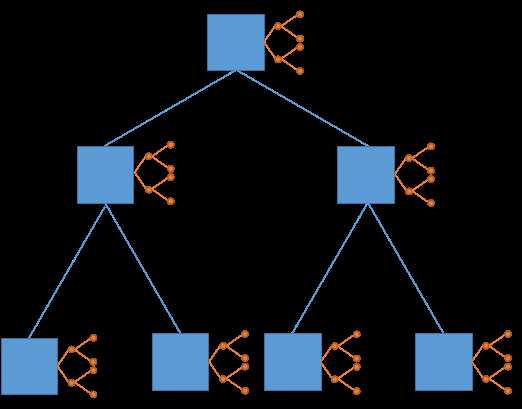
画完长这样(你们凑合看吧,作者已经半卒了)

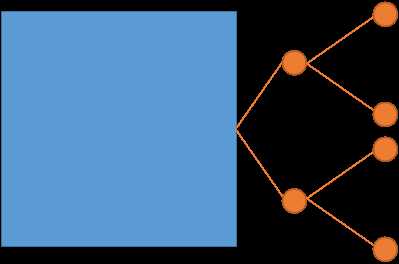
 局部放大图

 现在每个圆点代表真正的一个点

接下来的讲解以今天的题为例(题面就不放了)

先说区间修改

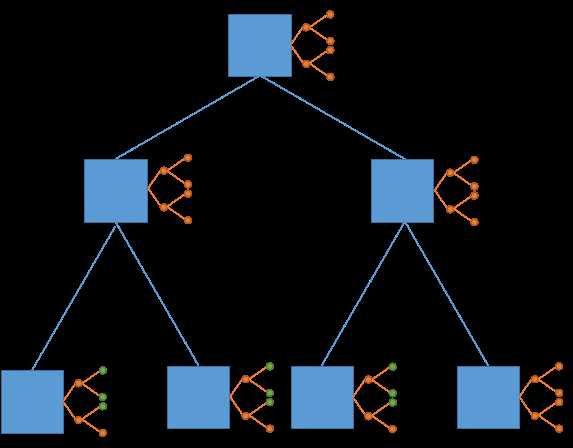
 假设我们现在要给图中的$9$个绿点赋值(仔细找,相信你能找到

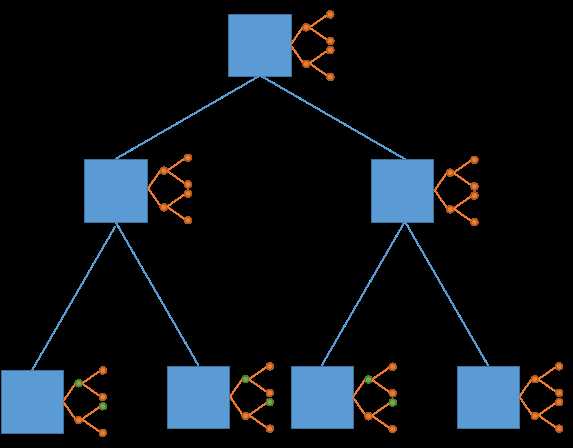
按照一维线段树的做法,我们会修改这六个绿点

但这是$\Theta (NlogN)$的,会$T$

我们可以是这对蓝点进行操作

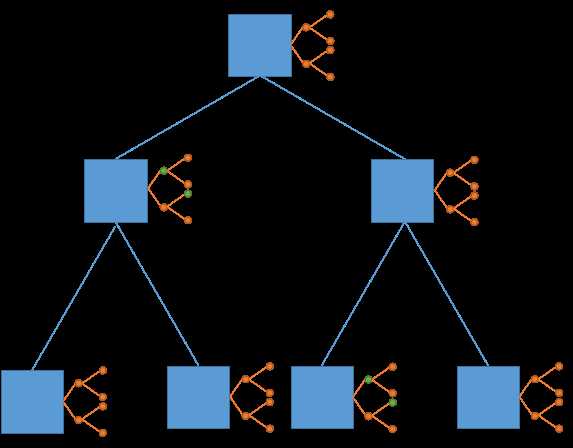
然后我们就可以只修改图中的四个绿点了

代码:

struct Tree
{
	struct tree
	{
		int tag;
	}t[maxn<<2];
	void down(int k)
	{
		int tmp=t[k].tag;
		t[l(k)].tag=max(t[l(k)].tag,tmp);
		t[r(k)].tag=max(t[r(k)].tag,tmp);
	}
	void change(int k,int l,int r,int L,int R,int v)
	{
		if(L<=l&&r<=R){t[k].tag=v;return;}
		down(k);int mid=(l+r)>>1;
		if(L<=mid)	change(l(k),l,mid,L,R,v);
		if(mid<R)	change(r(k),mid+1,r,L,R,v);
	}
}T[maxn<<2];

void change(int k,int l,int r,int L,int R,int ll,int rr,int v)
{
	if(L<=l&&r<=R){T[k].change(1,1,maxn-1,ll,rr,v);return;}
	int mid=(l+r)>>1;
	if(L<=mid)	change(l(k),l,mid,L,R,ll,rr,v);
	if(mid<R)	change(r(k),mid+1,r,L,R,ll,rr,v);
}

接下来是单点查询

 我们要查图中的绿点

 但是我们并不能只查询这一个点,因为下图中三个黄色的方块里都有关于这个绿点的信息

 所以我们只要一边向下走一边查询取$max/min$就可以了

代码:

int query(int k,int l,int r,int p)
{
	if(l==r)	return t[k].tag;
	down(k);int mid=(l+r)>>1;
	if(p<=mid)	return query(l(k),l,mid,p);
	else		return query(r(k),mid+1,r,p);
}

int query(int k,int l,int r,int p1,int p2)
{
	if(l==r){return T[k].query(1,1,maxn-1,p2);}
	int ans=T[k].query(1,1,maxn-1,p2),mid=(l+r)>>1;
	if(p1<=mid)	return max(ans,query(l(k),l,mid,p1,p2));
	else		return max(ans,query(r(k),mid+1,r,p1,p2));
}

以及完整代码:

struct Tree
{
	struct tree
	{
		int tag;
	}t[maxn<<2];
	void down(int k)
	{
		int tmp=t[k].tag;
		t[l(k)].tag=max(t[l(k)].tag,tmp);
		t[r(k)].tag=max(t[r(k)].tag,tmp);
	}
	void change(int k,int l,int r,int L,int R,int v)
	{
		if(L<=l&&r<=R){t[k].tag=v;return;}
		down(k);int mid=(l+r)>>1;
		if(L<=mid)	change(l(k),l,mid,L,R,v);
		if(mid<R)	change(r(k),mid+1,r,L,R,v);
	}
	int query(int k,int l,int r,int p)
	{
		if(l==r)	return t[k].tag;
		down(k);int mid=(l+r)>>1;
		if(p<=mid)	return query(l(k),l,mid,p);
		else		return query(r(k),mid+1,r,p);
	}
}T[maxn<<2];
void change(int k,int l,int r,int L,int R,int ll,int rr,int v)
{
	if(L<=l&&r<=R){T[k].change(1,1,maxn-1,ll,rr,v);return;}
	int mid=(l+r)>>1;
	if(L<=mid)	change(l(k),l,mid,L,R,ll,rr,v);
	if(mid<R)	change(r(k),mid+1,r,L,R,ll,rr,v);
}
int query(int k,int l,int r,int p1,int p2)
{
	if(l==r){return T[k].query(1,1,maxn-1,p2);}
	int ans=T[k].query(1,1,maxn-1,p2),mid=(l+r)>>1;
	if(p1<=mid)	return max(ans,query(l(k),l,mid,p1,p2));
	else		return max(ans,query(r(k),mid+1,r,p1,p2));
}

关于其他操作,有空在更(基本没空了

二维MLE线段树

标签：info   放大   tmp   idt   width   行操作   tag   nbsp   代码   

原文地址：https://www.cnblogs.com/ooovooo/p/11779048.html