标签:cti isp ring 遍历 dfs com 规模 ons 解释
你是一位系统管理员,手里有一份文件夹列表 folder,你的任务是要删除该列表中的所有 子文件夹,并以 任意顺序 返回剩下的文件夹。
我们这样定义「子文件夹」:
folder[i]?位于另一个文件夹?folder[j]?下,那么?folder[i]?就是?folder[j]?的子文件夹。文件夹的「路径」是由一个或多个按以下格式串联形成的字符串:
/?后跟一个或者多个小写英文字母。例如,/leetcode?和?/leetcode/problems?都是有效的路径,而空字符串和?/?不是。
示例 1:
输入: folder = ["/a","/a/b","/c/d","/c/d/e","/c/f"]
输出: ["/a","/c/d","/c/f"]
解释: "/a/b/" 是 "/a" 的子文件夹,而 "/c/d/e" 是 "/c/d" 的子文件夹。
示例 2:
输入: folder = ["/a","/a/b/c","/a/b/d"]
输出: ["/a"]
解释: 文件夹 "/a/b/c" 和 "/a/b/d/" 都会被删除,因为它们都是 "/a" 的子文件夹。
示例 3:
输入: folder = ["/a/b/c","/a/b/d","/a/b/ca"]
输出: ["/a/b/c","/a/b/ca","/a/b/d"]
提示:
1 <= folder.length?<= 4 * 10^42 <= folder[i].length <= 100folder[i]?只包含小写字母和 /folder[i]?总是以字符 /?起始路径两两比对, 有可能有三种情况:第一条路径是父路径, 第一条路径是子路径, 两条路径不相关
(A, B) --> (A->B)/(B->A)/(A<-!->B)
标记所有子路径, 在最后避开它们汇集所有父路径
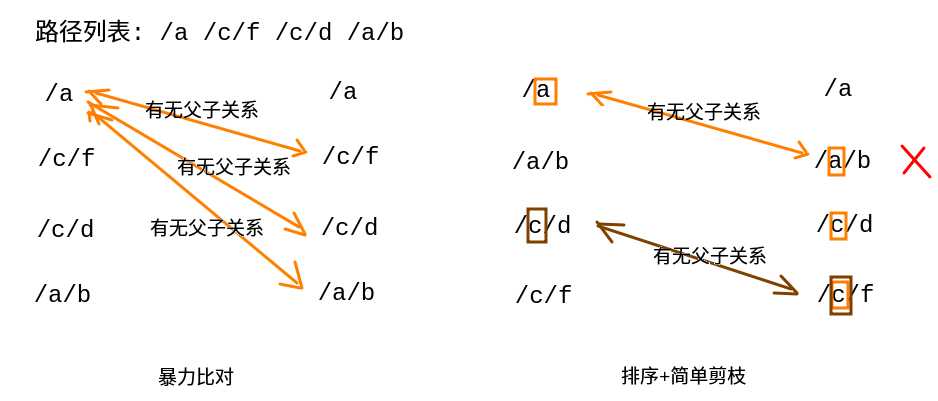
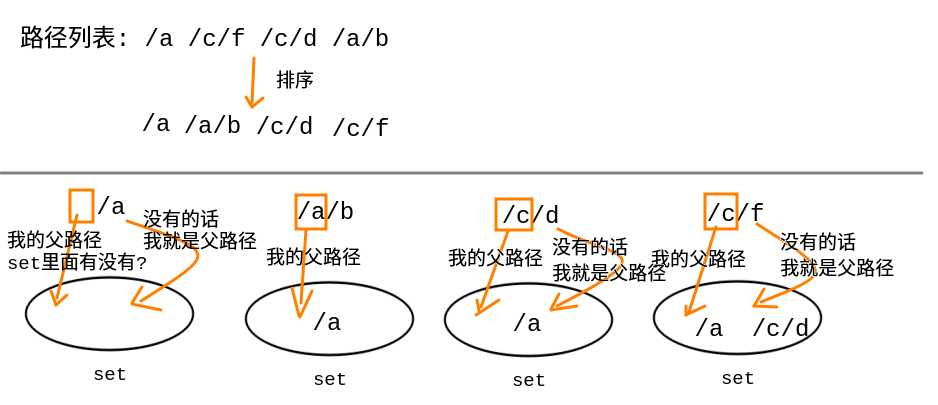
我们可以注意到排序后, 开始的路径都是父路径, 而排在其后的有比较大的可能是其子路径
接着每条路径逐个以/为前缀的路径比对集合中已有路径(这个可以优化)
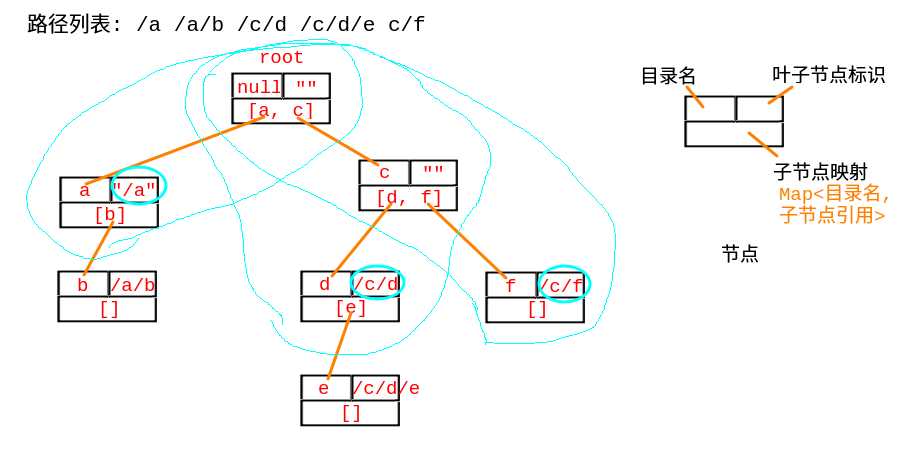
构建一颗以目录名为节点的词缀树, 深度遍历最近的叶子节点
class Solution {
public List<String> removeSubfolders(String[] folder) {
int len = folder.length;
if (len <= 1) {
return Collections.singletonList(folder[0]);
}
Arrays.sort(folder);
boolean[] delete = new boolean[len];
// 每两条路径进行比对 子路径删除(标记删除)
for (int i = 0; i < len; i++) {
for (int j = i + 1; j < len; j++) {
// 简单的剪枝 判断第二个字符是否相等作为 比较两路径的前提
if (!delete[i] && !delete[j] && (folder[i].charAt(1) == folder[j].charAt(1))) {
// 路径之间相互比较
if (aIsBParent(folder[i], folder[j])) {
delete[j] = true;
} else if (aIsBParent(folder[j], folder[i])) {
delete[i] = true;
}
}
}
}
// 没被标记删除的路径都是父路径
List<String> ans = new ArrayList<>();
for (int i = 0; i < len; i++) {
if (!delete[i]) {
ans.add(folder[i]);
}
}
return ans;
}
private boolean aIsBParent(String a, String b) {
// 如果a的路径比b的还长 则a必定不是b的父路径
if (a.length() >= b.length()) {
return false;
}
// 前缀是否相同 [/a/b] -> [/a/b]/c
return b.charAt(a.length()) == '/' && a.equals(b.substring(0, a.length()));
}
}class Solution {
public List<String> removeSubfolders(String[] folder) {
int len = folder.length;
Arrays.sort(folder);
Set<String> parents = new HashSet<>(len);
// 指定一条路径 切分其前缀路径比对已知父路径
for (String f : folder) {
boolean curIsParent = true;
int fLen = f.length();
// 因为是排序的 开始的路径必定是父路径(set存储)
for (int i = 1; i < fLen; i++) {
// 切分前缀路径 判断是否是已知父路径
if (f.charAt(i) == '/' && parents.contains(f.substring(0, i))) {
curIsParent = false;
}
}
if (curIsParent) {
parents.add(f);
}
}
return new ArrayList<>(parents);
}
}class Solution {
private class Node {
String name;
Map<String, Node> nexts;
Node() {
// 结尾标记 普通节点name="" 叶子节点name=path
name = "";
nexts = new HashMap<>();
}
@Override
/**
* debug时 可以显示内容
*/
public String toString() {
return "[" + name + "={" + nexts + "}]";
}
}
public List<String> removeSubfolders(String[] folder) {
// 建立词缀树
Node root = new Node();
for (String f : folder) {
String[] fs = f.split("/");
// 每次从根节点开始
Node cur = root;
for (String s : fs) {
if (!"".equals(s)) {
// 如果没有 则新建节点
if (!cur.nexts.containsKey(s)) {
cur.nexts.put(s, new Node());
}
// 切换到下一节点(键值为s)
cur = cur.nexts.get(s);
}
}
// 每条路径结尾处 使用name=f做标记
cur.name = f;
}
List<String> ans = new ArrayList<>();
// 深度优先遍历
dfs(root, ans);
return ans;
}
private void dfs(Node root, List<String> ans) {
// 最优先找到的叶子节点 就无需继续往下找了
if (!"".equals(root.name)) {
ans.add(root.name);
return;
}
// 遍历当前节点的所有下一节点
Set<String> set = root.nexts.keySet();
for (String s : set) {
// a -> b| -> /a/b
// a -> b| -> c -> /a/b/c [X]
// a -> c -> d -> /a/c/d
dfs(root.nexts.get(s), ans);
}
}
}标签:cti isp ring 遍历 dfs com 规模 ons 解释
原文地址:https://www.cnblogs.com/slowbirdoflsh/p/11779139.html